В четырехугольнике abcd диагонали пересекаются в точке м известно что ам 1

Геометрия | 5 — 9 классы

Диагонали четырехугольника ABCD пересекаются в точке M, причем AM = MC = BM = MD.

Определите тип четырехугольника.

Диагонали пересекаются в одной точке и делятся этой точкой пополам.

Такое свойство пренадлежит только такому четырехугольнику, как параллелограмм.

Следовательно, четырехугольник АВСД — параллелограмм.

Видео:№43. Диагонали четырёхугольника ABCD пересекаются в точке M. Известно, что углы BAC и ADC прямыеСкачать

Диагонали четырехугольника ABCD пересекаются в точке о известно что треугольники AOB = COD?

Диагонали четырехугольника ABCD пересекаются в точке о известно что треугольники AOB = COD.

Докажите что данный четырехугольник параллелограмм.

Видео:№382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольникСкачать

В четырехугольнике ABCD диагонали пересекаются в точке О?

В четырехугольнике ABCD диагонали пересекаются в точке О.

АС = 2дм, АО = 10см, BD = 1, 5дм, ВО = 7см.

Выясните, является ли ABCD параллелограммом?

Видео:№784. В паралеллограмме ABCD диагонали пересекаются в точке О, а М— точка на стороне AD, такая,Скачать

Вершины четырехугольника ABCDявляются серединами сторончетырехугольника, диагоналикоторого равны 6 дм ипересекаются под углом 60°?

Вершины четырехугольника ABCD

являются серединами сторон

которого равны 6 дм и

пересекаются под углом 60°.

Видео:№552. Диагонали трапеции ABCD с основаниями АВ и CD пересекаются в точке О. Найдите:Скачать

Диагонали четырехугольника ABCD пересекаются в точке М под углом 60 градусов, причем AM = MC = BM = MD?

Диагонали четырехугольника ABCD пересекаются в точке М под углом 60 градусов, причем AM = MC = BM = MD.

Определите вид четырехугольника.

Невозможно определить С решением пожалуйста.

Видео:ОГЭ 2024 Ященко 3 вариант ФИПИ школе полный разбор!Скачать

В четырехугольнике ABCD диагонали AC и BD равны?

В четырехугольнике ABCD диагонали AC и BD равны.

Является ли этот четырехугольник прямоугольником?

Видео:№748. Диагонали параллелограмма ABCD пересекаются в точке O. Равны ли векторы?Скачать

Пусть прямая, параллельная диагонали AC выпуклого четырехугольника ABCD и проходящая через середину его диагонали BD, пересекает сторону AD в точке E?

Пусть прямая, параллельная диагонали AC выпуклого четырехугольника ABCD и проходящая через середину его диагонали BD, пересекает сторону AD в точке E.

Докажите, что прямая EC делит площадь четырехугольника ABCD пополам.

Видео:ОГЭ без рекламы математика 11 и 12 вариант задача 25Скачать

В четырёхугольнике ABCD диагонали AC и BD пересекаются в точке O, причем OA = OB = OD?

В четырёхугольнике ABCD диагонали AC и BD пересекаются в точке O, причем OA = OB = OD.

Точки M и N — середины сторон AB и AD.

Докажите, что четырехугольник AMON — прямоугольник.

Видео:Геометрия Диагонали четырехугольника ABCD пересекаются в точке O Известно что угол A = углу D AO=ODСкачать

В выпуклом четырехугольнике ABCD пары противоположных сторон равны и параллельны, а диагонали пересекаются в точке О?

В выпуклом четырехугольнике ABCD пары противоположных сторон равны и параллельны, а диагонали пересекаются в точке О.

Найдите AC, если АО = 12.

Видео:№130. Через вершину В квадрата ABCD проведена прямая ВМ. Известно, что ∠MBA = ∠MBC=90°, МВ =m, АВСкачать

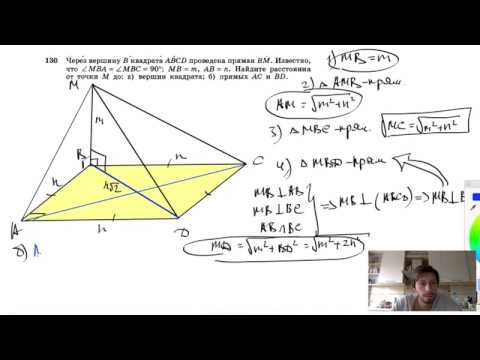
Диагональ АС невыпуклого четырехугольника ABCD разделяет этот четырехугольник на два треугольника, причем АС&gt ; ВС, АВ = AD, DC = CD, а прямые, содержащие диагонали четырехугольника, пересекаются в ?

Диагональ АС невыпуклого четырехугольника ABCD разделяет этот четырехугольник на два треугольника, причем АС&gt ; ВС, АВ = AD, DC = CD, а прямые, содержащие диагонали четырехугольника, пересекаются в точке О Сравните периметры пятиугольников BCODA и DCOBA.

Видео:ОГЭ 2020 задание 18Скачать

Четырехугольник abcd со сторонами ab = 25 и cd = 16 вписан в окружность?

Четырехугольник abcd со сторонами ab = 25 и cd = 16 вписан в окружность.

Диагонали ac и bd пересекаются в точке k , причем угол akb = 60 .

Найдите радиус окружности, описанной около этого четырехугольника.

На этой странице сайта вы найдете ответы на вопрос Диагонали четырехугольника ABCD пересекаются в точке M, причем AM = MC = BM = MD?, относящийся к категории Геометрия. Сложность вопроса соответствует базовым знаниям учеников 5 — 9 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.

Угол EAD = углу ВЕА = 32⁰ так как они накрест лежащие при параллельных ВС и АD. ΔАВС — равнобедренный, значит АЕ — биссектриса угла А. Угол А = 32⁰·2 = 64⁰ Так как у параллелограмма противоположные углы равны , то угол С = углу А = 64⁰, а угол В = ..

Обозначим сторону равностороннего треугольника как a. Высота является медианой (по свойству равностороннего треугольника), следовательно, высота делит сторону треугольника пополам. Тогда, по теореме Пифагора можем записать : a2 = (a / 2)2 + (97√3)2..

У меня так получилось, решила 2 способами и ответ один и тот же так что пиши как есть ибо другого ответа не может быть.

Обозначения : c — содержится ą — альфа Пусть МК — средняя линия трапеции. = > МК||ВС, ВС с ą = > MK||ą (Если прямая, не лежащая в данной плоскости, параллельна какой — нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости) Сред..

Ответ смотри на фото. Сорри, что карандашом, ручки под рукой не оказалось. В дано под цифрами написано то, что сказано только в одном из случаев. В решении — решение вопроса.

4) 180 — 45 = 135 5)180 — 40 — 90 = 50 7)90 т. К. угол прямой 8)ответ 40 т. К. угол DBЕ вертикален углу СBА.

Одну и только одну. Все три точки лежат на одной прямой.

Если три точки лежат на одной прямой, то другую провести нельзя (Ответ — одну прямую).

Б) 4 Т. К. каждая сторона треугольника должна быть меньше суммы двух других. Г)1 — не подходит, т. К. сказано, что длина не меньше 4.

УГОЛ cad = 30 следовательно угол bad = 30 (т. К. ad — биссектриса) угол А = 30 + 30 = 60 градусов угол А + угол В + угол С = 180 по теореме о сумме углов в треугольнике угол В = 180 — угол С — угол А угол В = 180 — 60 — 50 = 70 градусов ответ : угол..

Видео:№912. Диагонали параллелограмма ABCD пересекаются в точке О, М - середина отрезка АО. НайдитеСкачать

Проверочная работа «16 задание ПРОФИЛЬ ЕГЭ математика»

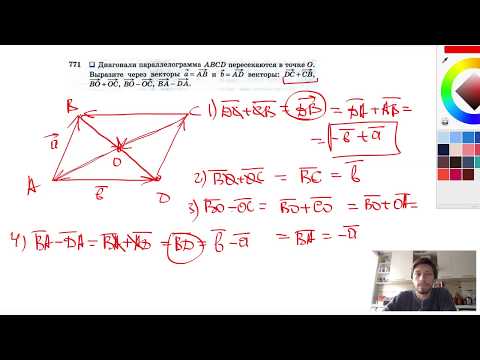
Видео:№771. В параллелограмме ABCD диагонали пересекаются в точке ОСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

ПРОФИЛЬ ЕГЭ математика

1. Окружность, вписанная в ромб ABCD , касается сторон CD и BC в точках M и Q соответственно. Прямые AM и BC пересекаются в точке P.

а) Докажите, что

б) Найдите угол если DM = 4 и MC = 9.

2. Две окружности касаются внешним образом в точке C. Прямая касается меньшей окружности в точке A, а большей — в точке B, отличной от A. Прямая AC вторично пересекает большую окружность в точке D, прямая BC вторично пересекает меньшую окружность в точке E.

а) Докажите, что прямая AE параллельна прямой BD.

б) Пусть L — отличная от D точка пересечения отрезка DE с большей окружностью. Найдите EL, если радиусы окружностей равны 2 и 5.

3. В равнобедренной трапеции ABCD длины оснований AD и BC соответственно равны 4 и 3. Точки M и N лежат на диагонали BD, причем точка M расположена между точками B и N, а отрезки AM и CN перпендикулярны диагонали BD.

а) Докажите, что BN : DM = 3 : 4.

б) Найдите длину отрезка CN, если известно, что BM : DN = 2 : 3.

4. Дан треугольник ABC. Серединный перпендикуляр к стороне AB пересекается с биссектрисой угла BAC в точке K, лежащей на стороне BC.

а) Докажите, что

б) Найдите радиус окружности, вписанной в треугольник AKB , если а площадь треугольника AKC равна

5. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекается в точке P, причём BC = CD.

а) Докажите, что

б) Найдите площадь треугольника COD, где O — центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, AB = 6, а

6. Две окружности касаются внутренним образом. Третья окружность касается первых двух и их линии центров.

а) Докажите, что периметр треугольника с вершинами в центрах трёх окружностей равен диаметру наибольшей из этих окружностей.

б) Найдите радиус третьей окружности, если известно, что радиусы первых двух равны 6 и 2.

7. На окружности с центром O и диаметром MN, равным 34, взята точка K на расстоянии 15 от этого диаметра. Хорда KE пересекает радиус OM в точке F под углом, равным

а) Докажите, что KF : FE = 125 : 29.

б) Найдите площадь треугольника KEN.

8. Прямая, проходящая через вершину В, прямоугольника ABCD, перпендикулярная диагонали АС и пересекает сторону АD в точке M, равноудаленной от вершин В и D.

а) Докажите, что ∠ ABM = ∠ DBC = ∠ MBD .

б) Найдите расстояние от точки О, точки пересечения диагоналей, до отрезка СМ, если BC = 42.

9. Две окружности касаются внутренним образом в точке С. Вершины A и B равнобедренного прямоугольного треугольника ABC c прямым углом C лежат на большей и меньшей окружностях соответственно. Прямая AC вторично пересекает меньшую окружность в точке D. Прямая BC вторично пересекает большую окружность в точке E.

а) Докажите, что AE параллельно BD.

б) Найдите AC, если радиусы окружностей равны 8 и 15.

10. Четырёхугольник ABCD вписан в окружность радиуса R = 10. Известно, что AB = BC = CD = 6.

а) Докажите,что прямые BC и AD параллельны.

ПРОФИЛЬ ЕГЭ математика

1. Прямая, проходящая через вершину В, прямоугольника ABCD, перпендикулярная диагонали АС и пересекает сторону АD в точке M, равноудаленной от вершин В и D.

а) Докажите, что BM и ВD делят угол В на три равных угла.

б) Найдите расстояние от точки пересечения диагоналей прямоугольника ABCD до прямой СМ, если

2. В прямоугольном треугольнике ABC проведена высота CH из вершины прямого угла. В треугольники ACH и BCH вписаны окружности с центрами O₁ и O₂ соответственно, касающиеся прямой CH в точках M и N соответственно.

а) Докажите, что прямые AO₁ и CO₂ перпендикулярны.

б) Найдите площадь четырёхугольника MO₁NO₂, если AC = 20 и BC = 15.

3. В прямоугольную трапецию ABCD с прямым углом при вершине A и острым углом при вершине D вписана окружность с центром O. Прямая DO пересекает сторону AB в точке M, а прямая CO пересекает сторону AD в точке K.

а) Докажите, что

б) Найдите площадь треугольника AOM, если и

4. Хорды AD, BE и CF окружности делят друг друга на три равные части.

а) Докажите, что эти хорды равны.

б) Найдите площадь шестиугольника ABCDEF, если точки A, B, C, D, E, F последовательно расположены на окружности, а радиус окружности равен

5. Окружность с центром О₁ касается оснований ВС и AD и боковой стороны АВ трапеции ABCD. Окружность с центром O₂ касается сторон ВС, CD и AD. Известно, что АВ = 10, ВС = 9, CD = 30, AD = 39.

а) Докажите, что прямая О₁О₂ параллельна основаниям трапеции АВСD.

6. Треугольник ABC прямоугольный с прямым углом C. Проведена высота CH. На сторонах AC и BC соответственно отмечены точки M и N так, что угол MHN прямой.

а) Докажите, что треугольники и ABC подобны.

б) Найдите BN, если

7. На гипотенузе AB и на катетах BC и AC прямоугольного треугольника ABC отмечены точки M, N и K соответственно, причем прямая KN параллельна прямой AB и BM = BN = Точка P — середина отрезка KN.

а) Докажите, что четырехугольник BCPM — равнобедренная трапеция.

б) Найдите площадь треугольника ABC, если и

8. Две окружности с центрами O₁ и O₂ и радиусами 3 и 4 пересекаются в точках A и B. Через точку A проведена прямая MK пересекающая обе окружности в точках M и K, причем точка A находится между ними.

а) Докажите, что треугольники BMK и O₁AO₂ подобны.

б) Найдите расстояние от точки B до прямой MK, если O₁O₂ = 5, MK = 7.

9. Две окружности пересекаются в точках P и Q. Прямая, проходящая через точку P, второй раз пересекает первую окружность в точке A, а вторую — в точке D. Прямая, проходящая через точку Q параллельно AD, второй раз пересекает первую окружность в точке B, а вторую — в точке C.

а) Докажите, что четырёхугольник ABCD — параллелограмм.

б) Найдите отношение CP : PB, если радиус первой окружности втрое больше радиуса второй.

10. Дан равнобедренный треугольник ABC с основанием AC. Вписанная в него окружность с центром O касается боковой стороны BC в точке P и пересекает биссектрису угла B в точке Q.

а) Докажите, что отрезки PQ и OC параллельны.

б) Найдите площадь треугольника OBC, если точка O делит высоту BD треугольника в отношении BO : OD = 3 : 1 и AC = 2.

ПРОФИЛЬ ЕГЭ математика

1. Четырёхугольник ABCD вписан в окружность радиуса R = 8. Известно, что AB = BC = CD = 12.

а) Докажите,что прямые BC и AD параллельны.

2. В треугольнике MPK биссектриса угла K пересекает сторону MP в точке A. Окружность, описанная около треугольника AMK пересекает сторону PK в точке B.

а) Докажите, что треугольник ABM равнобедренный.

б) Найдите площадь треугольника ABM, если MK = 9, PK = 6, MP = 5.

3. К окружности с диаметром AB = 10 проведена касательная BC так что Прямая AC вторично пересекает окружность в точке D. Точка E диаметрально противоположна точке D. Прямые ED и BC пересекаются в точке F.

а) Докажите, что

б) Найдите площадь треугольника FBE.

4. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны.

а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD, пересекаются на стороне AD.

б) Пусть N — точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM : MC = 3 : 4, а площадь четырёхугольника, стороны которого лежат на прямых AM, DM, BN и CN, равна 24.

5. Дана окружность с центром в точке O и радиусом 5. Точка K делит диаметр AD в отношении 1 : 9, считая от точки D. Через точку K проведена хорда BC перпендикулярно диаметру AD. На меньшей дуге AB окружности взята точка M.

а) Докажите, что BM · CM 2 .

б) Найдите площадь четырёхугольника ACBM, если дополнительно известно, что площадь треугольника BCM равна 24.

6. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD.

а) Докажите, что четырёхугольник DQOH — параллелограмм.

б) Найдите AD, если ∠ BAD = 75° и BC = 1.

7. В равнобедренном треугольнике ABC с углом 120° при вершине A проведена биссектриса BD. В треугольник ABC вписан прямоугольник DEFH так, что сторона FH лежит на отрезке BC, а вершина E — на отрезке AB.

а) Докажите, что FH = 2DH.

б) Найдите площадь прямоугольника DEFH, если AB = 4.

8. Из вершины С прямого угла прямоугольного треугольника ABC проведена высота CH.

а) Докажите, что отношение площадей кругов, построенных на отрезках AH и BH соответственно как на диаметрах равно

б) Пусть точка O₁ — центр окружности диаметра AH, вторично пересекающей отрезок AC в точке P, а точка O₂ — центр окружности с диаметром BH, вторично пересекающей отрезок BC в точке Q. Найдите площадь четырёхугольника O₁PQO₂, если

9. Дана трапеция KLMN с основаниями KN и LM. Окружности, построенные на боковых сторонах KL и MN как на диаметрах, пересекаются в точках A и B.

а) Докажите, что средняя линия трапеции лежит на серединном перпендикуляре к отрезку AB.

б) Найдите AB, если известно, что боковые стороны трапеции равны 26 и 28, а средняя линия трапеции равна 15.

10. На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE.

а) Докажите, что точки A, B, K и E лежат на одной окружности.

б) Найдите радиус этой окружности, если AB = 24, CH = 7.

ПРОФИЛЬ ЕГЭ математика

1. Четырёхугольник ABCD вписан в окружность. Диаметр CC₁ перпендикулярен стороне AD и пересекает её в точке M, а диаметр DD₁ перпендикулярен стороне AB и пересекает её в точке N.

а) Пусть AA₁ также диаметр окружности. Докажите, что

б) Найдите углы четырехугольника ABCD, если

2. Прямая, проходящая через вершину В, прямоугольника ABCD, перпендикулярная диагонали АС и пересекает сторону АD в точке M, равноудаленной от вершин В и D.

а) Докажите, что BM и ВD делят угол В на три равных угла.

б) Найдите расстояние от точки пересечения диагоналей прямоугольника ABCD до прямой СМ, если

3. Отрезок CH — высота прямоугольного треугольника ABC с прямым углом C. На катетах AC и BC выбраны точки M и N соответственно такие, что

a) Докажите, что треугольник MNH подобен треугольнику ABC.

б) Найдите CN, если BC = 2, AC = 4, CM = 1.

4. Хорды AD, BE и CF окружности делят друг друга на три равные части.

а) Докажите, что эти хорды равны.

б) Найдите площадь шестиугольника ABCDEF, если точки A, B, C, D, E последовательно расположены на окружности, а радиус окружности равен

5. Дана трапеция с диагоналями равными 6 и 8. Сумма оснований равна 10.

а) Докажите, что диагонали перпендикулярны.

б) Найдите высоту трапеции.

6. Две окружности касаются внутренним образом в точке A, причем меньшая окружность проходит через через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P.

а) Докажите, что прямые PQ и BC параллельны.

б) Известно, что sinAOC = Прямые PC и AQ пересекаются в точке K. Найдите отношение QK:KA.

7. Окружность проходит через вершины B и C треугольника ABC и пересекает AB и AC в точках C₁ и B₁ соответственно.

а) Докажите, что треугольник ABC подобен треугольнику AB₁C₁.

б) Найдите радиус данной окружности, если ∠ A = 45°, B₁C₁ = 6 и площадь треугольника AB₁C₁ в восемь раз меньше площади четырёхугольника BCB₁C₁.

8. В четырёхугольнике ABCD противоположные стороны не параллельны. Диагонали четырёхугольника ABCD пересекаются в точке O под прямым углом и образуют четыре подобных треугольника, у каждого из которых одна из вершин — точка O.

а) Докажите, что около четырёхугольника ABCD можно описать окружность.

б) Найдите радиус вписанной окружности, если AC = 10, BD = 26.

9. На катетах AC и BC прямоугольного треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M — середина гипотенузы AB, H — точка пересечения прямых CM и DK.

а) Докажите, что CMDK.

б) Найдите MH, если известно, что катеты треугольника ABC равны 30 и 40.

10. Окружность с центром О, вписанная в треугольник АВС, касается его сторон ВС, АВ и АС в точках K, L и М соответственно. Прямая КМ вторично пересекает в точке Р окружность радиуса АМ с центром А.

а) Докажите, что прямая АР параллельна прямой ВС.

б) Пусть AM = 3, CM = 2, Q — точка пересечения прямых КМ и АВ, а Т — такая точка на отрезке РQ, что Найдите QT.

Видео:Геометрия Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MBСкачать

В окружность вписан четырёхугольник ABCD, его диагонали АС и BD пересекаются в точке М. Докажите, что АМ/МС = АВ*АD/СВ*СD

Видео:№403. В прямоугольнике ABCD диагонали пересекаются в точке О. Найдите периметрСкачать

Ваш ответ

Видео:№344. Диагонали куба ABCDA1B1C1D1 пересекаются в точке О. Найдите число k такое,Скачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,739
• разное 16,824

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

💡 Видео

егэ векторы решу егэ все задания №2 профильСкачать

25)В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O. Докажите, что площади треСкачать

Четырёхугольник ABCD со сторонами AB = 40 и CD = 10 вписан в окружность. Диагонали #огэ #математикаСкачать

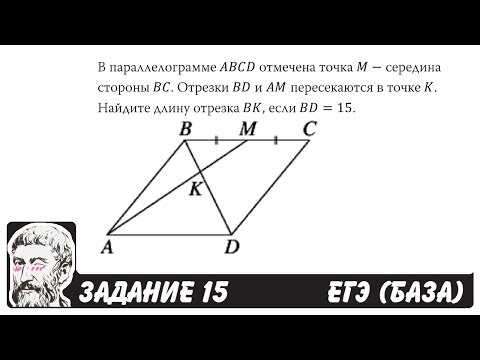
🔴 В параллелограмме ABCD отмечена точка M ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

§-5 № 1-58 - Геометрия 8 класс Мерзляк углубленный уровеньСкачать