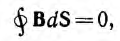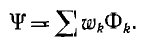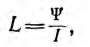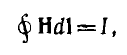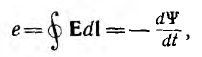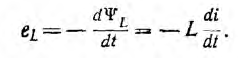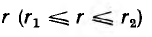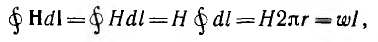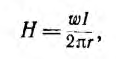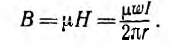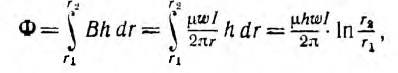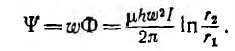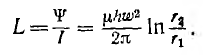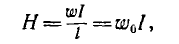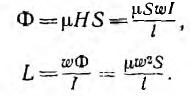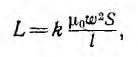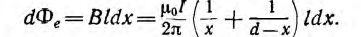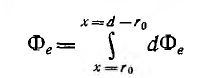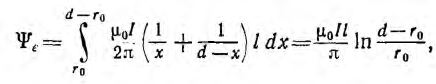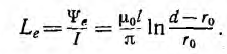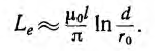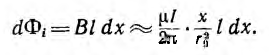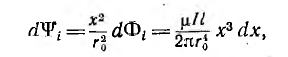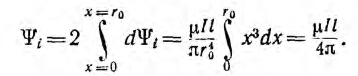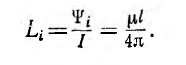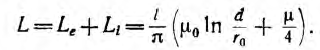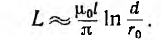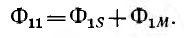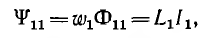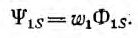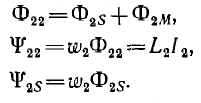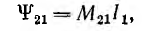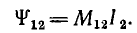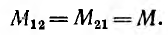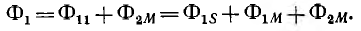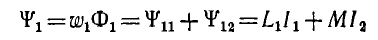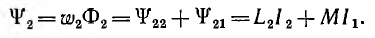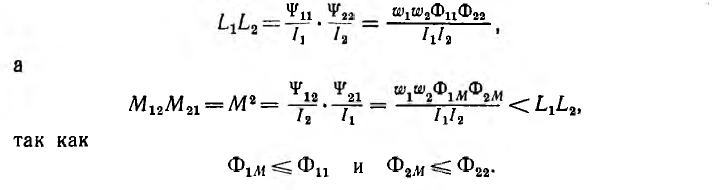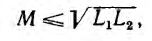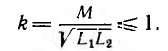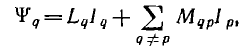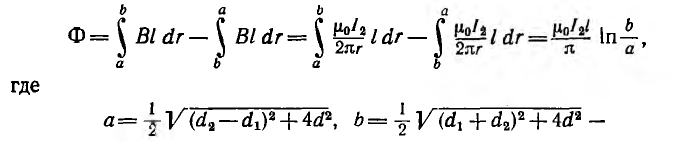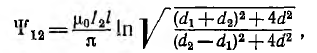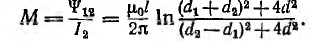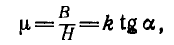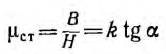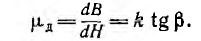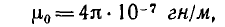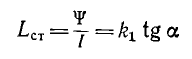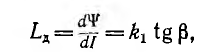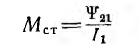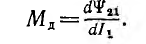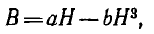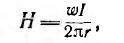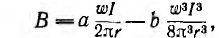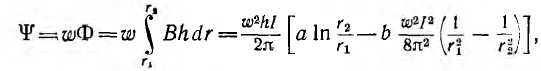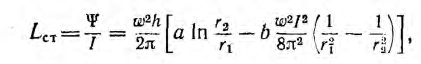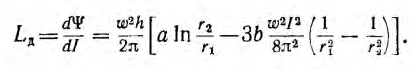Расчет вектора магнитной индукции для тороида

Построим картину линий напряженности магнитного ноля вокруг бесконечного прямолинейного проводника с током (рис. 22.4). По аналогии с циркуляцией вектора напряженности электростатического поля (17.7) введем понятие циркуляции вектора напряженности магнитного

Для простоты сначала в качестве контура выберем окружность, совпадающую с одной из линий напряженности магнитного поля. В соответствии с формулой (22.12) напряженность на этой окружности является константой. А в соответствии с рис. 22.4 вектор напряженности направлен но касательной к окружности. Эти соображения позволяют вычислить циркуляцию:

Принцип суперпозиции магнитных полей и рассуждения, аналогичные предпринятым в разделе о циркуляции вектора напряженности электростатического поля, позволяют обобщить полученное выражение на несколько токов и произвольный контур:

Это и есть теорема о циркуляции вектора напряженности магнитного поля: циркуляция вектора напряженности магнитного поля по произвольному контуру равна алгебраической сумме токов, охватываемых контуром.

Теперь домножением обеих частей уравнения (22.18) на р₀ц получим теорему о циркуляции вектора магнитной индукции:

Искусство применения теоремы о циркуляции состоит в выборе удобного для расчета контура.

Применим теорему о циркуляции для вычисления напряженности магнитного поля длинного соленоида с током I. Соленоид — это провод, равномерно навитый на цилиндрический каркас (рис. 22.5). Будем считать, что диаметр каркаса много меньше его длины, а шаг плотной намотки (расстояние между витками) много меньше диаметра. При этих условиях поле внутри соленоида, как будет очевидно из результата, много больше поля вне соленоида и достаточно однородно (заметим, что поле вне соленоида можно определить по формуле для магнитного поля прямого тока (22.12)). Из соображений симметрии поле внутри соленоида направлено вдоль оси соленоида. Пусть плотность намотки витков (количество витков на единицу длины каркаса) равна п витков на метр.

В соответствии с рис 22.5 выберем прямоугольный контур, у которого малые (по сравнению с большими сторонами длиной /) стороны 2—3 и 4—1 в точке протыкания каркаса перпендикулярны каркасу, большая сторона 1—2 находится внутри каркаса, большая сторона 3—4 находится вне каркаса. В такой ситуации в циркуляции, состоящей из четырех интегралов по отрезкам, доминирует составляющая по отрезку 1—2. Составляющими по отрезкам 2—3 и 4—1 можно пренебречь вследствие малости отрезков. Составляющей по отрезку 3—4 можно пренебречь вследствие перпендикулярности (приблизительно) поля отрезку и малости этого поля. Внутрь контура попадает п! витков с током. Таким образом, циркуляция сводится к отрезку 1—2, но в соответствии с формулой (22.19) определяется полным током nil внутри контура:

Отметим, что это поле достаточно однородно по диаметру каркаса, ведь стороны 2—3 и 4— 1 малы лишь по сравнению с длиной каркаса, но могут быть сравнимы с диаметром каркаса и углубляться внутрь каркаса на любое расстояние.

Соответственно, магнитная индукция внутри длинного соленоида равна

Вычислим теперь магнитное иоле тороида. Тороид — это провод, навитый на тор (бублик). Его можно получить из соленоида, изогнув его в кольцевую катушку (рис. 22.6). Поле тороида похоже на поле соленоида, и линии напряженности тороида параллельны оси тороида. Покажем это, выбрав в качестве контура для вычисления циркуляции окружность радиуса г внутри тора с центром в центре тороида. По теореме о циркуляции для тороида с полным числом витков провода N

откуда магнитное поле внутри тороида

Если контур проходит вне тороида, то внутри него токи отсутствуют, т.е.

и поле из теоремы о циркуляции равно нулю. Таким образом, магнитное поле тороида локализовано внутри тороида и спадает по мере удаления от центра симметрии.

Если тороид тонкий и его радиус R

г много больше радиуса витка, то несложно получить, что поле внутри тороида (22.24) дается формулой, аналогичной формуле для поля соленоида (22.22):

Видео:Билет №16 "Теорема о циркуляции и теорема Гаусса для магнитного поля"Скачать

Индуктивность и ее расчет

Содержание:

Индуктивность и ее расчет:

Основным соотношением для магнитного поля является принцип непрерывности магнитного потока:

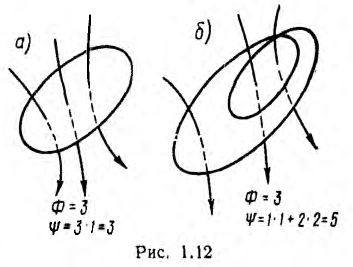
На рис. 1.12, а и б проиллюстрировано различие между потоком и
потокосцеплением, причем число линий в условном масштабе равно
величине потока.

Индукция измеряется в тесла (тл), магнитный поток и потокосцепление — в веберах (вб).
Индуктивность уединенного контура, равная отношению потокосцепления к току:

пропорциональна магнитной проницаемости среды, в которой он находится, и определяется конфигурацией контура. Единицей индуктивности является генри (гн).
Для расчета индуктивности контура необходимо предварительно рассчитать его магнитное поле по основному соотношению — закону полного тока:

устанавливающему связь между напряженностью магнитного поля 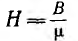и полным током I — алгебраической суммой токов, сцепляющихся с путем интегрирования. При этом положительное направление тока I связано с направлением dI обхода правилом правого винта.
Напряженность магнитного поля измеряется в а/м, магнитная проницаемость — в гн/м.
Если потокосцепление контура изменяется во времени, то в контуре появляется э. д. с. индукции е, величина и направление которой определяется законом электромагнитной индукции:

где Е — вектор напряженности наведенного в контуре электрического поля.
Таким образом, закон электромагнитной индукции связывает между собой изменение магнитного поля с возникающим электрическим полем.
Максвеллом было постулировано обобщение этого закона, заключающееся в том, что электрическое поле возникает при изменении магнитного поля в любой среде, а не только в проводящем контуре.

Закон электромагнитной индукции, открытый Фарадеем в 1831 г., был дополнен Ленцем в 1832— 1834 гг. Им было установлено общее правило: з. д. с. индукции всегда стремится создать ток, направленный так, чтобы препятствовать изменению потока, сцепляющегося с контуром.
При изменении тока в контуре изменяется потокосцепление ψ_L созданное этим током, и в контуре наводится э. д. с. самоиндукции

Видео:Теорема Ампера о циркуляции магнитной индукции. Магнитное поле соленоида и тороида в вакууме.Скачать

Индуктивность тороида и соленоида

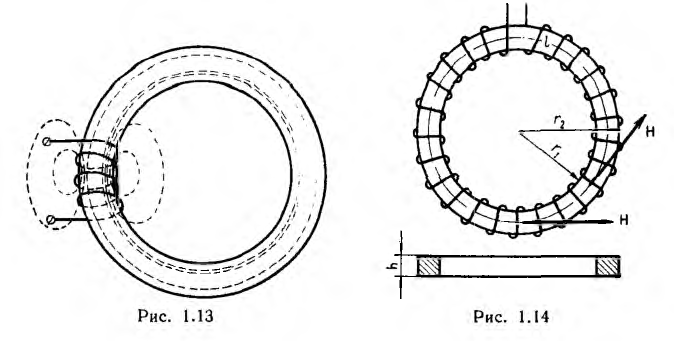
Если на кольцевой сердечник — тороид, выполненный из материала проницаемостью µ > µ₀, нанести обмотку не по всей его длине (рис. 1.13), то только часть потока проходит по сердечнику, остальная часть — поток рассеяния — замыкается в воздухе. Тороид же, содержащий витки, плотно и равномерно распределенные по всей длине сердечника (рис. 1.14), замечателен тем, что практически весь магнитный поток сосредоточивается в сердечнике, т. е. потока рассеяния нет. Линии вектора напряженности поля представляют собой окружности, сцепляющиеся со всеми витками. Ввиду симметрии напряженность поля в каждой точке окружности по величине постоянна; по направлению она совпадает с касательной к окружности.

Тороиды широко применяются в трансформаторах, магнитных усилителях и электроизмерительных приборах.

Пусть тороид имеет прямоугольное сечение высотой Н, с радиусами г₁ и г₂, магнитная проницаемость материала µ.

По закону полного тока для окружности с радиусом

т. е. напряженность поля убывает по мере приближения к наружному краю тороида. Это в равной мере относится и к индукции

Поток в сердечнике тороида

Отсюда индуктивность тороида

Если расчет вести для средней линии I и приближенно считать поле в тороиде распределенным равномерно, то напряженность

где w₀ — число витков на единицу длины, а магнитный поток и индуктивность, соответственно,

Обычно в реальных тороидах отношение 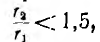что приводит при этих приближенных формулах к погрешности, не превышающей 1,2 %. Последняя формула для индуктивности может быть применена и к длинному соленоиду, рассматриваемому как часть тороида бесконечно большого радиуса. Для соленоида конечной длины µ=µ₀

где k µ₀. Посередине между проводами поле минимально, но в нуль не обращается. Поле также не равно нулю на осях проводов.

На внутренней стороне проводов напряженность поля и индукция больше, чем на внешней. В отличие от напряженности поля индукция имеет разрыв у поверхности проводов. Для вычисления индуктивности линии необходимо найти потокосцепление. Элементарный поток, проходящий через площадку Idx в воздухе между проводами,

Весь поток между проводами — внешний поток

одновременно является внешним потокосцеплением, так как сцепляется с контуром один раз. Поэтому

а соответствующая ему внешняя индуктивность

Для большинства линий расстояние d между проводами значительно превышает радиус r₀ проводов. В этом случае

Для определения внутренней индуктивности, соответствующей внутреннему потоку, при d > r₀ поле внутри провода линии может вычисляться как поле уединенного провода, так как поле, создаваемое вторым проводом внутри первого, по сравнению с полем первого, пренебрежимо мало. Тогда элементарный поток внутри провода

Так как поток dФ_i охватывает не весь ток, а только его часть [см. формулу (1.3)], элементарное потокосцепление

Весь поток между проводами — внешний поток

Соответственно, внутренняя индуктивность

Суммарная индуктивность линии

При медных или алюминиевых проводах (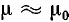) в большинстве случаев вторым членом можно пренебречь по сравнению с первым и тогда

Для стальных проводов (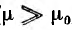) основной частью потока является
внутренний поток и индуктивность

практически не будет зависеть от расстояния между проводами.

Видео:Урок 271. Модуль вектора магнитной индукции. Закон АмпераСкачать

Взаимоиндуктивность и ее расчет

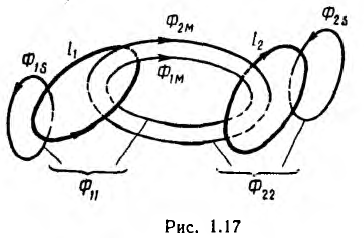
Для двух контуров, имеющих w₁ и w₂ витков с токами I₁ и I₂ (рис. 1.17), поток первого контура, определяемый током этого контура, — поток самоиндукции Ф_1l—может быть разложен на поток рассеяния Ф_1s, пронизывающий только этот контур, и поток взаимоиндукции Ф_1m, пронизывающий также и второй контур:

Потокосцепление, соответствующее потоку Ф₁₁ (при условии, что этот поток пронизывает все витки первого контура, равно

а потокосцепление рассеяния

Аналогично для второго контура

Потокосцепление второго контура, определяемое током первого,

а потокосцепление первого контура, определяемое током второго,

Можно показать, что

Величина M называется взаимоиндуктивностью и определяется конфигурацией контуров, их взаимным расположением и магнитной проницаемостью среды. Взаимоиндуктивность также измеряется в генри (гн).
Суммарный поток, пронизывающий первый контур,

Суммарное потокосцепление первого контура

и соответственно для второго контура

В этих алгебраических суммах первый член всегда положителен, а знак перед вторым членом определяется направлением токов в контурах; положительный знак соответствует случаю совпадения направлений потоков Ф_1м и Ф_2м (см. рис. 1.17).
Из изложенного видно, что

Таким образом, взаимоиндуктивность и индуктивности всегда удовлетворяют неравенству

а используемый в технических расчетах коэффициент связи двух контуров

Аналогично, в системе многих контуров потокосцепление контура определяется токами всех контуров:

где L_q — индуктивность q-то контура, М_qp = М_рq — взаимоиндуктивность q- и р-го контуров. Общий прием расчета взаимоиндуктивности контуров заключается
в нахождении потокосцепления, пронизывающего контур q, но созданного током р-го контура, и делении его на этот ток.

Видео:Магнитное поле соленоидаСкачать

Взаимоиндуктивность двух параллельных двухпроводных линий

Пусть две параллельные двухпроводные линии расположены симметрично так, как это было показано на рис. 1.4. При условии d> г₀ внутренним потоком в проводах по сравнению с внешним можно пренебречь.
Магнитный поток, пронизывающий первую линию и созданный током I₂ второй, может быть найден как сумма потоков, создаваемых каждым из проводов второй линии в отдельности.
Тогда магнитный поток, пронизывающий первую линию,

расстояния от провода линии 1 до проводов линии 2 .

Магнитный поток Ф одновременно является потокосцеплением 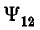первой линии, так как сцепляется с ней один раз; поэтому

Для уменьшения коэффициента связи между линиями связи l и передачи 2 применяют транспозицию линии связи, заключающуюся в перекрещивании проводов линии связи через равные расстояния; тогда суммарное потокосцепление 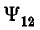будет равно нулю.

Видео:магн поле внутри соленоидаСкачать

Линейные и нелинейные катушки индуктивности

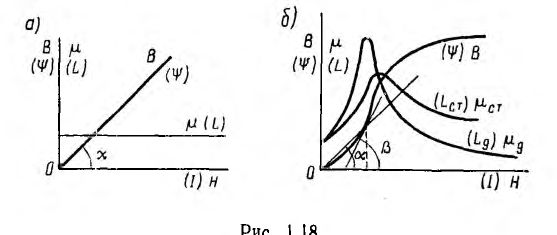
У линейных материалов магнитная проницаемость µ, не зависит от напряженности поля и характеристика 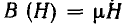для них изображается прямой линией (рис. 1.18, а). Магнитная проницаемость пропорциональна тангенсу угла а наклона этой прямой:

где k — масштабный коэффициент.

К нелинейным материалам относятся ферромагнетик и — железо, никель, кобальт и гадолиний. Важное значение в электротехнике имеют первые три элемента, главным образом в виде сплавов. У нелинейных материалов магнитная проницаемость очень велика 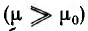и зависит от напряженности поля.

Подобно нелинейным диэлектрикам по кривой первоначальногo намагничивания В (Н) (рис. 1.18, б) могут быть определены статическая магнитная проницаемость

и дифференциальная, а при быстрых изменениях поля — динамическая магнитная проницаемость

На рис. 1.18, б эти проницаемости представлены в функции напряженности поля. Максимальные значения магнитной проницаемости в очень чистом железе и в некоторых сплавах, например в пермаллое (сплав железа и-никеля с различными присадками), в сотни тысяч раз превышают магнитную постоянную равную

магнитной проницаемости вакуума.

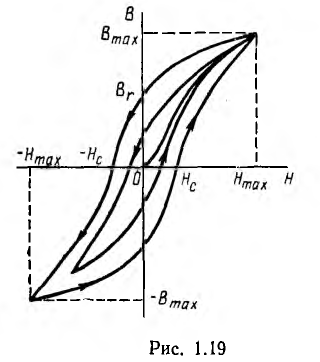
В переменных магнитных полях в ферромагнетиках имеет место явление магнитного гистерезиса (рис. 1.19), заключающееся в несовпадении кривой В (Н) при возрастании напряженности поля с кривой при убывании поля.

Кривая, соединяющая вершины петель гистерезиса, называется основной кривой намагничивания и практически совпадает с кривой первоначального намагничивания, Ферромагнитные свойства зависят от температуры и проявляются лишь в определенном ее интервале.

Для расчета индуктивности основной является зависимость потокосцепления ψ от тока I, называемая веберамперной характеристикой.

В зависимости от материала сердечника тороиды по виду своей веберамперной характеристики будут также линейными или нелинейными. В качестве примера рассматривается нелинейный тороид.

Для тороида 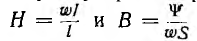и веберамперные характеристики ψ (I) в соответствующем масштабе совпадают с кривыми В (H); поэтому прямая и кривые на рис. 1.18 а и б соответствуют также веберамперным характеристикам при величинах, указанных в скобках.

Для нелинейных тороидов вводятся понятия статической индуктивности

и дифференциальной, а также динамической индуктивности

являющихся функциями тока (см. рис. 1.18, б); для линейных тороидов эти индуктивности совпадают.

Аналогично индуктивностям в нелинейных системах контуров вводятся статическая взаимоиндуктивность

и дифференциальная, взаимоиндуктивность, а также динамическая

Видео:ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ сила Ампера правило левой рукиСкачать

Индуктивность нелинейного тороида

Расчет нелинейного тороида может быть произведен, если задана зависимость В (H) или µ(H). Так как эти зависимости теоретически не выводятся, то для приближенного решения подбирают по кривой В(H) аппроксимирующую функцию.

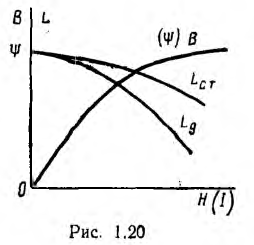
Пусть аппроксимирующая функция для характеристики В (H) (рис. 1.20)
материала сердечника тороида будет

где а и b — постоянные.

Так как для тороида с ферромагнитным однородным cердечником напряженность поля по-прежнему определяется формулой

то индукция будет равна

откуда статическая индуктивность

а дифференциальная индуктивность

Кривые зависимости этих индуктивностей от тока представлены
на рис. 1.20.

• Энергия в электрических цепях
• Линейные электрические цепи
• Нелинейные электрические цепи
• Магнитные цепи и их расчёт
• Электрическая ёмкость и ее расчет
• Линейные н нелинейные диэлектрики и конденсаторы
• Сопротивление и его расчет
• Линейные и нелинейные резисторы

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Поток вектора магнитной индукцииСкачать

Закон полного тока для магнитного поля

В электрических цепях всегда присутствует магнитное поле, которое оказывает электромагнитное взаимодействие с токами этих цепей. Данный фактор учитывается при расчетах цепей, а закон полного тока для магнитного поля является инструментом для подобных вычислений.

Если поднести магнитную стрелку к проводнику, по которому течёт ток, её положение изменится. Это говорит о наличии вокруг проводника кроме электрического ещё и магнитного поля. В результате многочисленных исследований электромагнитных явлений установлено, что существует взаимное влияние полей, имеющих электрическую и магнитную природу.

Видео:Магнитное поле. Магнитная индукция | Физика 11 класс #1 | ИнфоурокСкачать

Физический смысл закона

Рассмотрим упрощённый вариант влияния магнитной индукции на электрическое поле. Для этого представим себе два параллельных проводника, по которым циркулируют постоянные токи, например, I₁ и I₂. Вблизи этих проводников образуется поле, которое мысленно можно ограничить неким контуром L – воображаемой замкнутой фигурой, плоскость которой пересекает потоки движущихся зарядов.

В пределах плоскости, охватываемой контуром L, формируется магнитное поле, напряжённость которого распределена в соответствии с направлениями токов. При этом циркуляция вектора магнитного поля в плоскости замкнутого контура прямо пропорциональна сумме токов, пронзающих данный контур. Полный электрический ток равен векторной сумме его составляющих:

Направления векторов I₁ и I₂ определяется по правилу буравчика.

Приведённые выше рассуждения можно рассматривать в качестве примера изображающего упрощённую модель частного случая рассматриваемого закона. В действительности же, процессы взаимного влияния магнитных и электрических полей намного сложнее, и они описываются интегральными и дифференциальными уравнениями Максвелла.

Видео:Урок 287. Индуктивность контура (катушки). Явление самоиндукцииСкачать

Упрощенный подход

Выразить закон в дифференциальном представлении довольно сложно. Потребуется вводить дополнительные компоненты. Необходимо учитывать влияние молекулярных токов. Наличие вихревых токов является причиной образования магнитного вихревого поля в пределах контура.

Вектор электрического смещения сравним с вектором напряжённости присутствующего магнитного поля H. При этом Ориентация вектора смещения зависит от быстроты изменения магнитной индукции.

Для упрощения вычислений на практике часто пользуются формулами закона для магнитного поля полных токов, представленных в виде суммирования предельно малых участков контура, с учётом влияния вихревых полей. При реализации этого метода контур мысленно разбивают на бесконечно малые отрезки. На этих отрезках проводники считаются прямолинейными, а магнитное поле на таких участках контура считают однородным.

На одном дискретном участке вектор напряженности U_m определяется по формуле: U_m= H_L×ΔL, где H_L– циркуляция вектора напряжённости на участке ΔL контура L. Тогда суммарная напряжённость U_L вдоль всего контура вычисляется по формуле: U_L= Σ H_L× ΔL.

Видео:Электромагнитная индукция. Простыми словамиСкачать

Закон в интегральном представлении

Рассмотрим бесконечно прямой проводник, по которому циркулирует электрический ток, образующий поле, ограниченное контуром в виде окружности. Плоскость, пронизывающая проводник, – это круг, очерчённый линией данной окружности (см. рис. 1).

Рис. 1. Поле бесконечно прямого тока

Воспользуемся методом разбиения контура на мизерные участки dl (элементарные векторы длины контура). Пусть φ – угол между векторами dl и B. В нашем случае, при суммировании отрезков, вектор индукции B поворачивается так, что он очерчивает круг, то есть угол φ → 2π.

Из теоремы Остроградского-Гаусса вытекает формула:

Учитывая, что cos φ = 1,

Данная формула – постулат, подтверждённый экспериментально. Согласно этому постулату, циркуляция вектора B по окружности, то есть по замкнутому контуру, равна μ₀I, где μ₀ = 1/c 2 ε₀ – магнитная постоянная.

Ориентация вектора dB определяется путём применения правила буравчика. Это направление всегда перпендикулярно вектору плотности. Если проводников будет несколько (например, N), тогда

Каждый ток, с учётом знака, необходимо учитывать такое количество раз, которое соответствует числу его охватов контуром.

Ток берётся со знаком «+», если он по направлению обхода образует правовинтовую систему. При этом, отрицательным считается ток противоположного направления.

Заметим, что формула справедлива только для вакуума. В обычных условиях необходимо учитывать проницаемость среды.

Если ток распределён в пространстве (произвольный ток), тогда

где S – натянутая на контур поверхность, j – объёмная плотность тока. С учётом последнего выражения, формулу полного тока в вакууме можно записать:

Рис. 2. Иллюстрация закона для вакуума

1. Закон справедлив не только для бесконечно прямолинейного проводника, но и для контуров, произвольной конфигурации.
2. Циркуляция вектора магнитной индукции B сориентированного вдоль магнитных линий, всегда отлична от нуля.
3. Ненулевая циркуляция свидетельствует о том, что магнитное поле прямолинейного, бесконечно длинного проводника не потенциально. Такое поле называют вихревым, либо соленоидным.

Видео:Индукция магнитного поля | Физика 9 класс #37 | ИнфоурокСкачать

Влияние среды

На результат взаимодействия магнитных потоков и постоянных токов влияет среда. Вещества обладают магнитной проницаемостью в потоке вектора индукции, что вносит коррективы на взаимодействие магнитной среды с токами проводимости. В однородной изотопной среде, где значение вектора электромагнитной индукции одинаково во всех точках, векторы B и H связаны между собой следующим соотношением:

где H — напряжённость магнитного поля, символом μ обозначена магнитная проницаемость.

Носители электрических зарядов создают собственные микротоки. Циркуляция вектора, характеризующего электростатическое поле, всегда нулевая. Поэтому электростатические поля, в отличие от магнитных, являются потенциальными.

Вектор B отображает результирующее значение полей макро- и микротоков. Линии электростатической индукции всегда остаются замкнутыми, в том числе и на положительных зарядах.

Рис. 3. Закон полного тока в веществе

Для полей, которые действуют в среде, состоящей из разных веществ, необходимо учитывать микротоки, характерные именно для конкретных структур, образующих данную среду.

Утверждение, изложенное выше, верно для полей соленоидов или любой другой структуры, обладающей свойствами конечной магнитной проницаемости.

Видео:Теорема о циркуляции вектора магнитной индукции. Магнитный поток.Скачать

Торойд

В электротехнике часто приходится иметь дело с катушками разных видов и размеров. Катушка, образованная витками намотанными на сердечник тороидальной формы (в виде бублика), называется тороидом. Важными характеристиками сердечника тора являются его радиусы — внутренний (R₁) и внешний (R₂).

Поле внутри соленоида на расстоянии r от центра равно:

Видео:ЭМ Л21. 2023. Закон полного тока. Теорема Гаусса для магн поля. Тороид и соленоид. Магнитный моментСкачать

Выводы

На основании изложенного, приходим к заключению:

1. Закон полного тока устанавливает зависимость между напряжённостью магнитного поля и перемещением в этом поле электрических зарядов.
2. Действие закона распространяется на все среды, при допустимых плотностях тока.
3. Закон также выполняется в полях постоянных магнитов.

При вычислениях не имеет значения, какую формулу мы используем – суть закона остаётся неизменной: он выражает взаимодействия, которые происходят между токами и создаваемыми ими магнитными полями, пронизывающими замкнутый контур.

Выводы закона учитываются при конструировании электромагнитных устройств. Наличие завихрений в электромагнитных полях приводит к снижению КПД. Кроме того, вихревые поля негативно влияют на работоспособность электронных элементов, расположенных в зоне их действий.

Конструкторы электротехнических приборов стремятся свести к минимуму таких влияний. Например, вместо обычных соленоидов применяют тороидальные катушки, за пределами которых отсутствуют электромагнитные поля.

💥 Видео

ЧК_МИФ РАЗБОР ЗАДАЧИ НА РАСЧЕТ МАГНИТНОГО ПОЛЯ ТОРОИДАЛЬНОЙ КАТУШКИСкачать

Вектор магнитной индукции, принцип суперпозиции магнитных полейСкачать

Магнитная индукция и напряженность магнитного поляСкачать

14. Вектор магнитной индукции. Правило правого винта.Скачать

Расчет магнитной проницаемости сердечниковСкачать

Линии магнитной индукции наглядно. Правило правой рукиСкачать

Модуль вектора магнитной индукцииСкачать