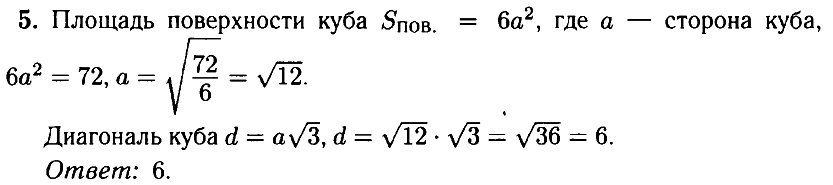Умение выполнять действия с геометрическими фигурами координатами и векторами (6 видео)

ЕГЭ для VIP

Подготовке к ЕГЭ

Содержание

ЕГЭ по математике Профиль. Задание 5
ЕГЭ Профиль. Задание № 5
АЛГОРИТМ ВЫПОЛНЕНИЯ
Задачи на Прямоугольный параллепипед
Задачи на Составные многогранники
Задачи на Призмы
Задачи на Пирамиды
Задачи на Цилиндры
Задачи на Конусы
Задачи на Шары
Задачи на Комбинации многогранников и тел вращения
Тренировочные задания с самопроверкой
Уметь выполнять действия с геометрическими фигурами, координатами и векторами 1.Решать планиметрические задачи на нахождение геометрических величин (длин, — презентация
Похожие презентации
Презентация на тему: » Уметь выполнять действия с геометрическими фигурами, координатами и векторами 1.Решать планиметрические задачи на нахождение геометрических величин (длин,» — Транскрипт:
Набор упражнений для подготовки к ЕГЭ
💡 Видео

Видео:ОГЭ по Математике. Задание 17. Задача 2Скачать

ЕГЭ по математике Профиль. Задание 5

ЕГЭ по математике Профиль. Задание 5: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

ЕГЭ Профиль. Задание № 5

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задание № 5 рассчитано на умение решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объёмов), использовать при выполнении знание свойств основных пространственных тел, применять планиметрические факты и методы.

Задание состоит из текстовой задачи и рисунка. Рассматриваются простые пространственные тела: куб, прямоугольный параллелепипед, правильная пирамида, правильная призма. Ответом является конечная десятичная дробь или целое число.

План выполнения:

Внимательно прочитайте задачу.
При необходимости выполните на черновике чертёж и дополнительные построения.
Сделайте на черновике необходимые вычисления.
Запишите полученное число в поле ответа КИМ и бланк ответов № 1.

Задачи на Прямоугольный параллепипед

Для решения подобных задач необходимо повторить свойства куба и прямоугольного параллелепипеда, формулы для вычисления площади поверхности, объёма этих тел.

Задача № 5 (1). Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 5. Объём параллелепипеда равен 30. Найдите площадь его поверхности.

Решение: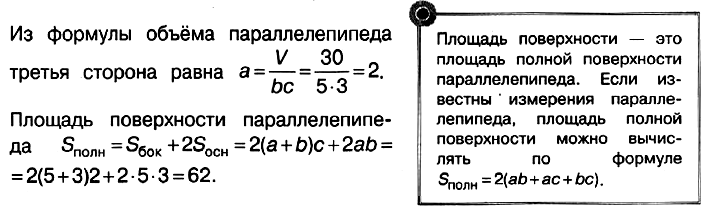

Ответ: 62.

Задачи на Составные многогранники

Задача № 5 (2). Найдите объём многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые.

Решение: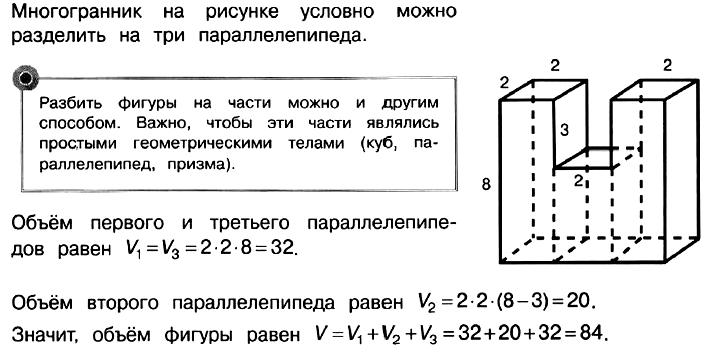

Ответ: 84.

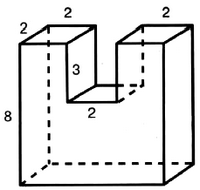
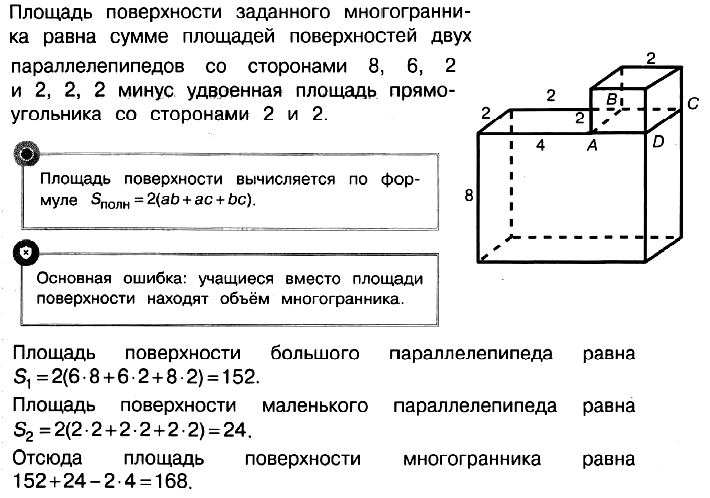
Задача № 5 (3). Найдите площадь поверхности многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые.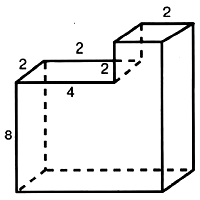

Решение:

Ответ: 168.

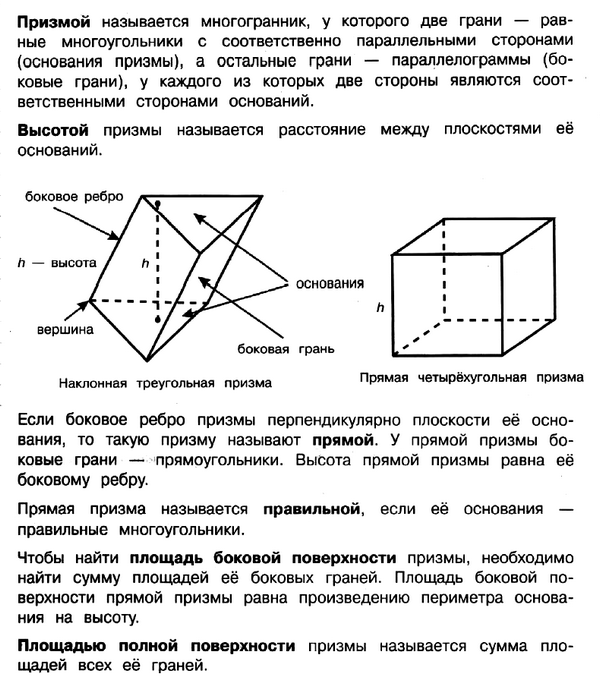
Задачи на Призмы

Для решения задач этого типа необходимо повторить свойства призмы, формулы для вычисления площади поверхности и объёма призмы.

Задача № 5 (4). В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых рёбер на 6 и 8. Найдите площадь боковой поверхности этой призмы.

Решение: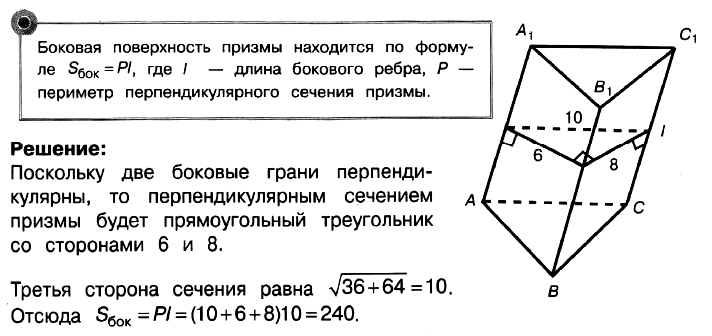

Ответ: 240.

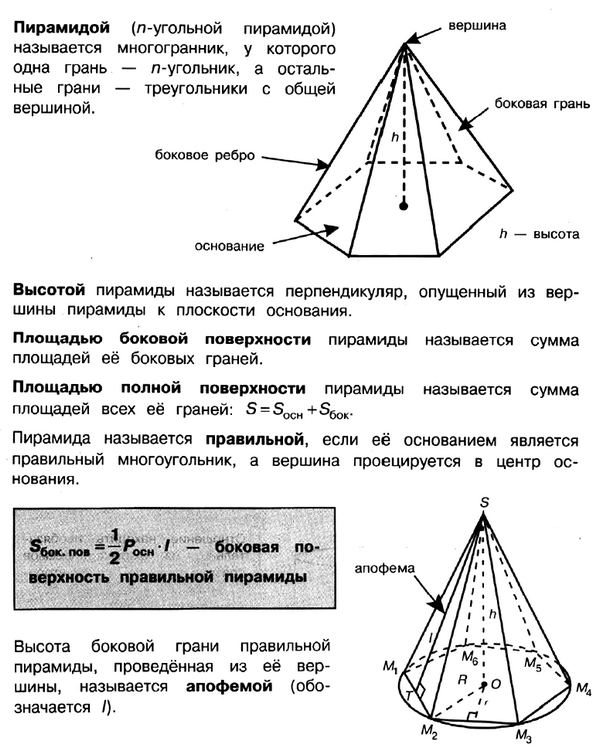
Задачи на Пирамиды

При подготовке нужно повторить основные свойства пирамиды, формулы для вычисления площади поверхности и объёма пирамиды.

Задача № 5 (5). Основание пирамиды — треугольник, у которого длины двух сторон равны 2 и 6, а угол между этими сторонами составляет 30°. Вычислите объём пирамиды, если её высота равна 3.

Решение:

Ответ: 3.

Задачи на Цилиндры

Для решения задач этого типа необходимо повторить формулы вычисления площади круга, длины окружности, площади поверхности цилиндра, объёма цилиндра.

Задача № 5 (6). Радиус основания цилиндра увеличили в 3 раза, а его высоту уменьшили в 4 раза. Во сколько раз увеличится объём цилиндра?

Решение: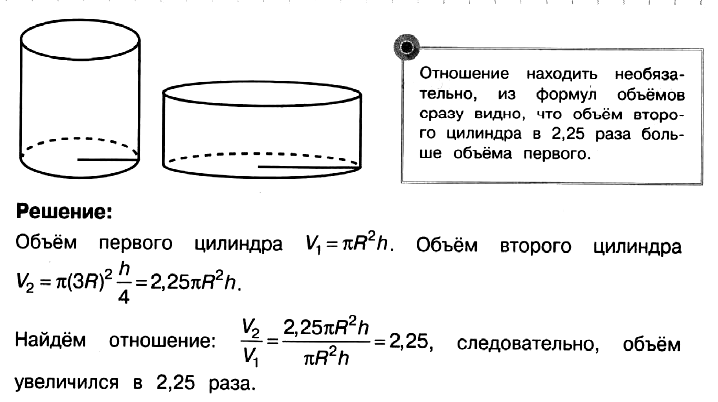

Ответ: 2,25.

Задачи на Конусы

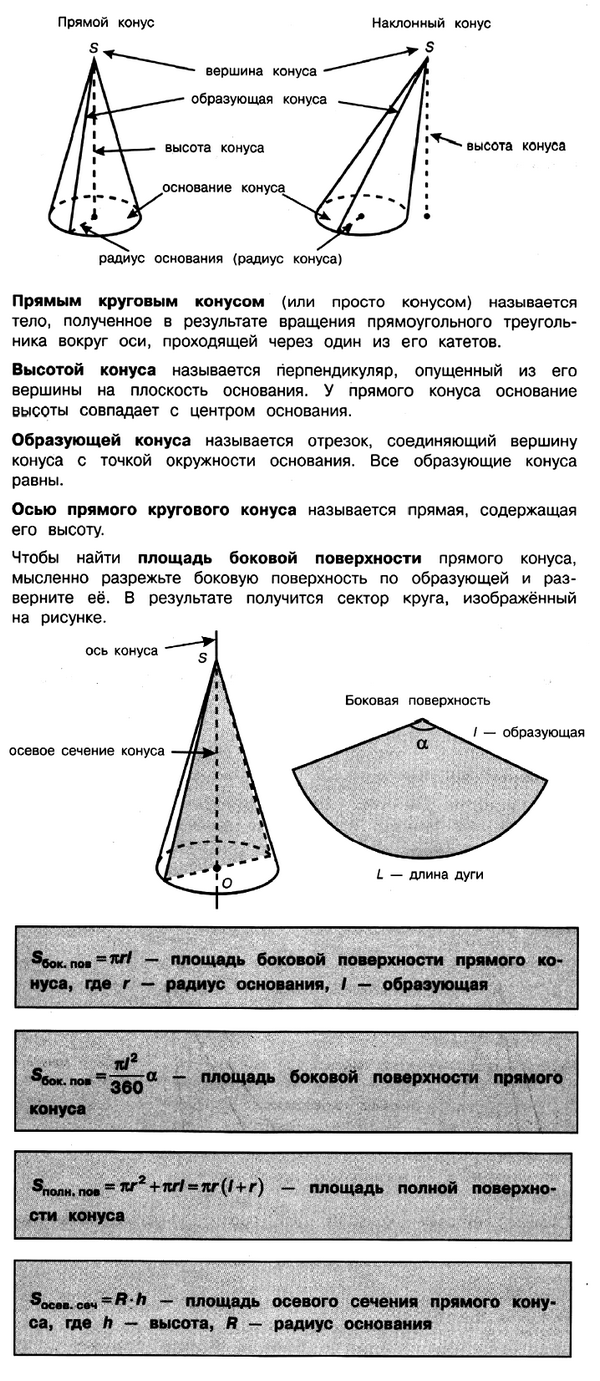
При подготовке необходимо повторить свойства конуса, формулы для вычисления площади поверхности и объёма конуса, площади круга и длины окружности.

Задача № 5 (7). Диаметр основания конуса равен 12, угол при вершине осевого сечения равен 90°. Вычислите объём конуса, делённый на π.

Решение: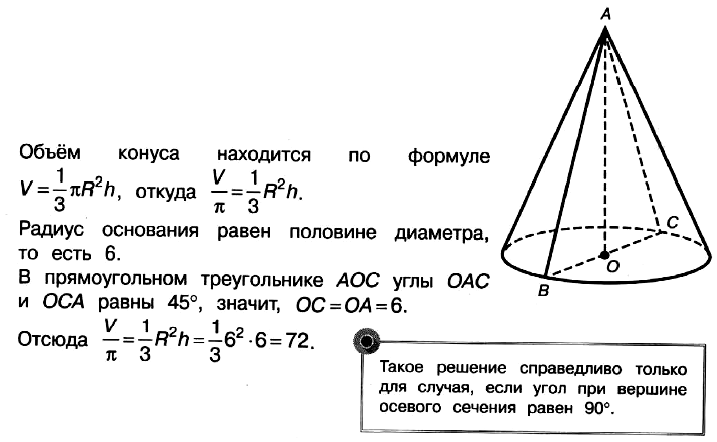

Ответ: 72.

Задачи на Шары

Для решения задач этого типа необходимо повторить формулы для вычисления площади круга, длины окружности, площади поверхности шара, объёма шара.

Задача № 5 (8). Площадь сечения шара плоскостью равна 36π см 2 . Найдите радиус шара, если плоскость находится на расстоянии 8 см от центра шара.

Решение:

Ответ: 10.

Задачи на Комбинации многогранников
и тел вращения

Задача № 5 (9). В основании прямой призмы лежит прямоугольный треугольник с катетами 3 и 4. Боковые рёбра призмы равны 4/π. Найдите объём цилиндра, описанного около этой призмы.

Решение:

Ответ: 25.

Задача № 5 (10). Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 15. Найдите площадь поверхности шара.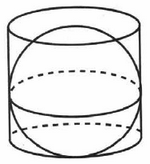

Решение:

Ответ: 10.

Задача № 5 (11). Объём конуса равен 7π см 3 . Найдите объём правильной четырёхугольной пирамиды, вписанной в конус.

Решение: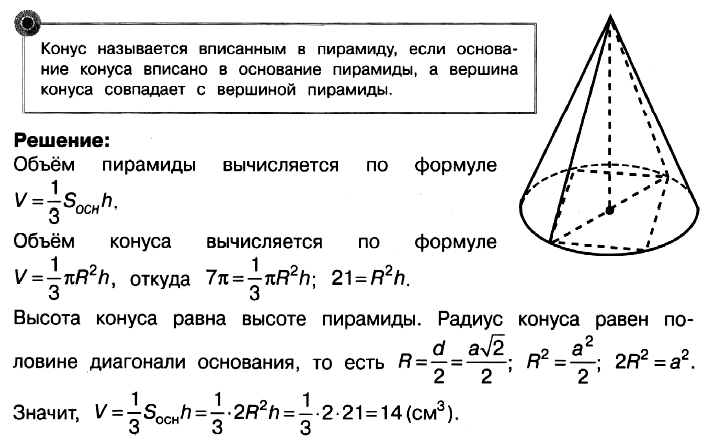

Ответ: 14.

Задача № 5 (12). Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 20. Найдите объём конуса.

Решение:

Ответ: 5.

Тренировочные задания с самопроверкой

№ 5.1. Площадь поверхности куба равна 72 (см. рис.). Найдите его диагональ.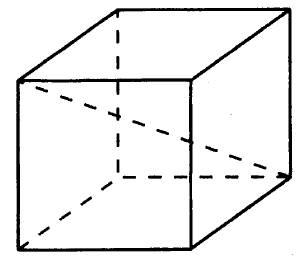

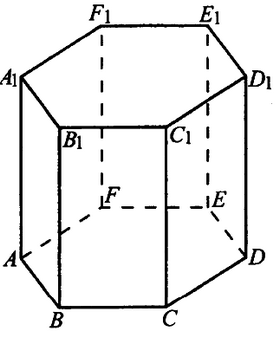
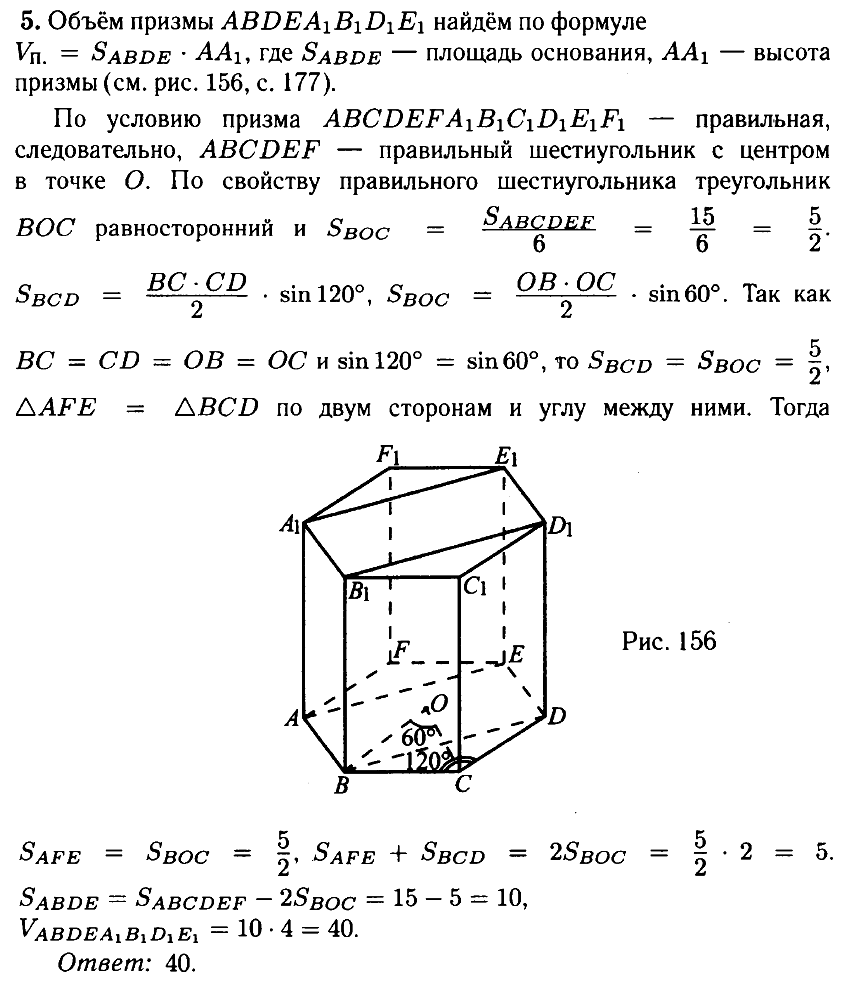
№ 5.2. Найдите объём многогранника, вершинами которого являются точки А, В, D, Е, А₁, В₁, D₁, E₁ правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁ (см. рис.). Площадь основания призмы равна 15, а боковое ребро равно 4.

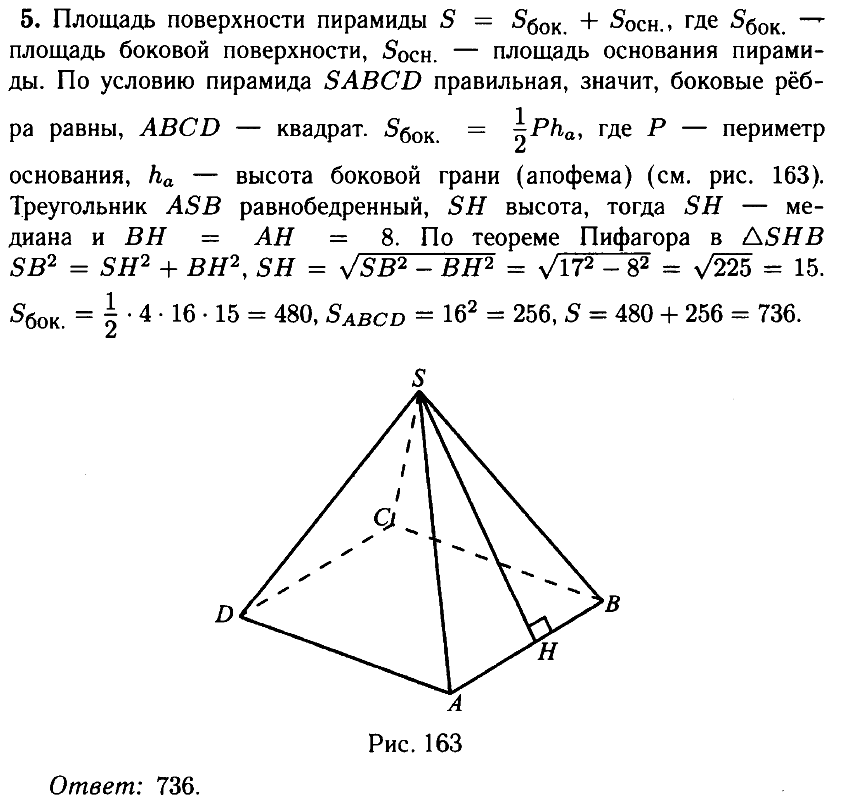
№ 5.3. Стороны основания правильной четырёхугольной пирамиды равны 16, боковые рёбра равны 17 (см. рис.). Найдите площадь поверхности этой пирамиды.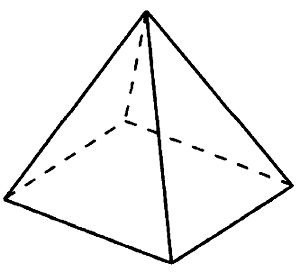

№ 5.4. В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты (см. рис.). Объём жидкости равен 60 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?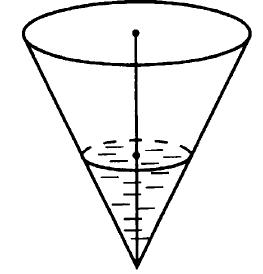

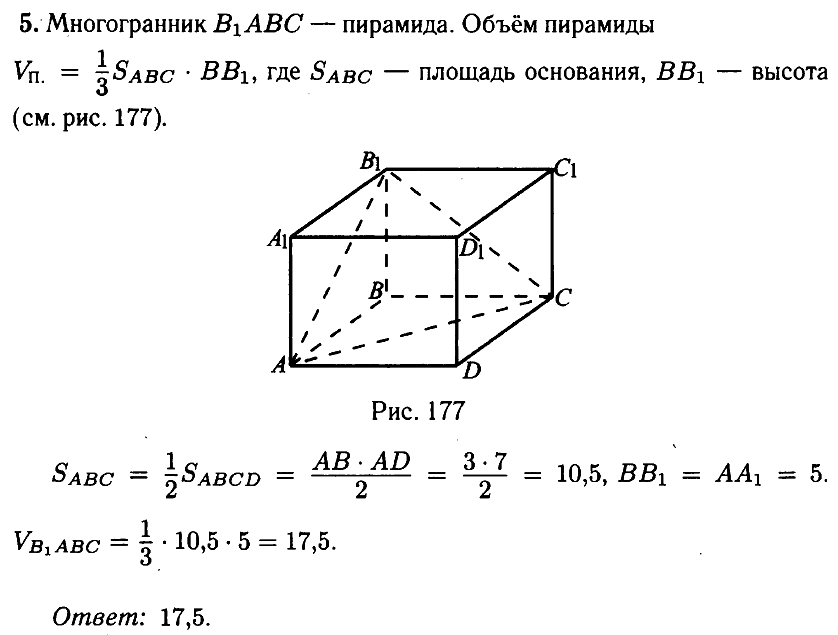
№ 5.5. Найдите объём многогранника, вершинами которого являются точки А, В, С, В прямоугольного параллелепипеда ABCDA₁B₁C₁D₁, у которого АВ = 3, AD = 7, АА₁ = 5 (см. рис.).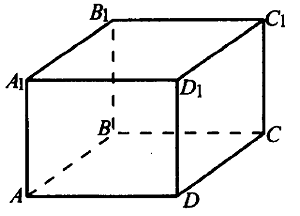

Вы смотрели: ЕГЭ по математике Профиль. Задание 5: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Уметь выполнять действия с геометрическими фигурами, координатами и векторами 1.Решать планиметрические задачи на нахождение геометрических величин (длин, — презентация

Презентация была опубликована 8 лет назад пользователемИлья Шудегов

Презентация на тему: » Уметь выполнять действия с геометрическими фигурами, координатами и векторами 1.Решать планиметрические задачи на нахождение геометрических величин (длин,» — Транскрипт:

2 Уметь выполнять действия с геометрическими фигурами, координатами и векторами 1.Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей) 2.Решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов); использовать при решении стереометрических задач планиметрические факты и методы 3.Определять координаты точки; проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами

3 Повторение: а b а

4 a haha a bc a b Площадь треугольника

5 Площадь трапеции h a b Площадь параллелограмма h a

6 Площадь круга r Площадь кругового сектора rα

7 Длина окружности r Длина дуги окружности rα

8 Сложение векторов Правило треугольника: А В С Для любых трех точек A,B,C имеет место равенство

10 1.Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см x 1 см. Ответ дайте в квадратных сантиметрах.

11 S2S2 S3S3 S1S1 S

12 Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

13 2. Найдите (в см 2 ) площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.).

15 4. Найдите площадь треугольника, вершины которого имеют координаты (0;0), (10;8), (8;10).

16 5. Найдите площадь параллелограмма, вершины которого имеют координаты (1;7), (4;1), (4;4), (1;10).

17 6. Найдите (в см2) площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). В ответе запишите S/π.

18 7. Найдите площадь сектора круга радиуса, центральный угол которого равен 90˚.

19 8. Периметр треугольника равен 88, а радиус вписанной окружности равен 10. Найдите площадь этого треугольника.

20 9. Площадь сектора круга радиуса 15 равна 105. Найдите длину его дуги.

21 10. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150. Боковая сторона треугольника равна 19. Найдите площадь этого треугольника

22 11. Найдите угловой коэффициент прямой, проходящей через точки с координатами (-2;0)и (0;11). Общее уравнение прямой: y = kx + b 12. Найдите площадь прямоугольника, если его периметр равен 116, а отношение соседних сторон равно 4:25. a b a=4k b= 25k P=2(4k+25k)=58k 58k=116k=2 a=8 b= 50 S=8·50= 400

23 13. Площадь параллелограмма равна 36, две его стороны равны 12 и 24. Найдите большую высоту этого параллелограмма S=ha 36=h· 12 h=3

24 14. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30 градусов. Найдите боковую сторону треугольника, если его площадь равна ˚ h aa

25 15. Найдите ординату точки пересечения прямой, заданной уравнением 21х-20у=60, с осью Oy. 18. Две стороны прямоугольника ABCD равны 9 и 40. Найдите длину суммы векторов АВ и AD.

26 19. Найдите абсциссу центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (5; 10), (5;2), (-1;2), (-1;10).

27 Диагонали ромба ABCD равны 48 и 55. Найдите длину вектора. А В С D

28 Найдите площадь трапеции, вершины которой имеют координаты (2;1), (10;1), (9;9), (6;9). Реши самостоятельно:

29 1.Средняя линия и высота трапеции равны соответственно 36 и 4. Найдите площадь трапеции. 2.Угол при вершине, противолежащей основанию равнобедренного треугольника, равен. Найдите боковую сторону треугольника, если его площадь равна Площадь сектора круга радиуса 41 равна 123. Найдите длину его дуги. 4. Найдите угловой коэффициент прямой, проходящей через точки с координатами и.

30 5. Точки O(0,0). являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей. 6. Найдите абсциссу центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно. 7. Диагонали ромба ABCD равны 42 и 56. Найдите длину вектора. 8. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

31 9. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Видео:Готовимся к ЕГЭ по математике. Решение заданий 16. Часть 1. ДидактикаСкачать

Набор упражнений для подготовки к ЕГЭ

Разделы: Математика

1. Задания типа В1.

Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни.

Проверяемые требования. Анализировать реальные числовые данные; осуществлять практические расчеты по формулам, пользоваться оценкой и прикидкой при практических расчетах.

Задания типа В2.

Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни.

Проверяемые требования. Определять значение функции по значению аргумента при различных

способах задания функции; описывать по графику поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения; строить графики изученных функций.

Задания типа В3.

Уметь решать уравнения и неравенства.

Проверяемые требования. Решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы.

Задания типа В4.

Уметь выполнять вычисления и преобразования.

Проверяемые требования. Вычислять значения числовых и буквенных выражений, осуществляя

необходимые подстановки и преобразования; проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции.

Задания типа В5.

Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни.

Проверяемые требования. Решать прикладные задачи, в том числе социально-экономического и

физического характера, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.

Задание типа В6.

Уметь выполнять действия с геометрическими фигурами, координатами и векторами.

Проверяемые требования. Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей). Моделировать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, аппарата алгебры; решать практические задачи, связанные с нахождением геометрических величин.

Задания типа В7.

Уметь выполнять вычисления и преобразования .

Проверяемые требования. Выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени, степени с рациональным показателем, логарифма.

Задания типа В8.

Уметь выполнять действия с функциями.

Проверяемые требования. Определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения; строить графики изученных функций. Вычислять производные и первообразные элементарных функций.

Задания типа В9.

Уметь выполнять действия с геометрическими фигурами, координатами и векторами.

Проверяемые требования. Решать простейшие стереометрические задачи на нахождение стреометрических величин (длин, углов, площадей, объемов); использовать при решении стереометрических задач планиметрические факты и методы.

Задания типа В10.

Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни.

Проверяемые требования. Решать прикладные задачи, в том числе социально-экономического и физического характера, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.

11. Задания типа В11.

Уметь выполнять действия с функциями .

Проверяемые требования. Исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций.

Задания типа В12.

Уметь строить и исследовать простейшие математические модели.

Задания типа С1.

Уметь решать уравнения и неравенства.

Проверяемые требования. Решать рациональные, иррациональные, показательные,тригонометрические и логарифмические уравнения, их системы. Решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков; использовать для приближенного решения уравнений и неравенств графический метод.

Задания типа С2.

Уметь выполнять действия с геометрическими фигурами, координатами и векторами.

Проверяемые требования. Решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов); использовать при решении стереометрических задач планиметрические факты и методы. Определять координаты точки; проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами.

Задания типа С3.

Уметь решать уравнения и неравенства.

Проверяемые требования. Решать рациональные, показательные и логарифмические неравенства, их системы.

Задания типа С4.

Уметь выполнять действия с геометрическими фигурами, координатами и векторами .

Проверяемые требования. Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей).

Задания типа С5.

Уметь решать уравнения и неравенства.

Задания типа С6.

Уметь строить и исследовать простейшие математические модели.

Проверяемые требования. Моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры. Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать логически некорректные рассуждения.