Для любых двух скрещивающихся прямых существует плоскость которой они обе параллельны (8 видео)

Скрещивающиеся прямые. Проведение через одну из скрещивающихся прямых плоскости, параллельной другой прямой

Содержание

ИПР Аксиомы стереометрии, параллельность прямых и плоскостей
Просмотр содержимого документа «ИПР Аксиомы стереометрии, параллельность прямых и плоскостей»
2. Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми
📽️ Видео

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы рассмотрим определение скрещивающихся прямых и докажем теорему – признак скрещивающихся прямых. Далее рассмотрим три случая взаимного расположения двух прямых в пространстве. Докажем теорему о том, что через каждую из скрещивающихся прямых можно провести плоскость, параллельную другой прямой.
В конце урока решим несколько задач в тетраэдре на скрещиваемость прямых.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

ИПР Аксиомы стереометрии, параллельность прямых и плоскостей

В файле представлена итоговая проверочная работа по теме «Аксиомы стереометрии, параллельность прямых и плоскостей» в двух вариантах по учебнику «Геометрия 10-11» автора Л.С. Атанасян. Эту работу проводила в конце учебного года при повторении изученного материала

Просмотр содержимого документа
«ИПР Аксиомы стереометрии, параллельность прямых и плоскостей»

Итоговая проверочная работа

Аксиомы стереометрии, параллельность прямых и плоскостей

Определите, верно ли утверждение:

Если две прямые не скрещиваются, то они лежат в одной плоскости.

Для любых двух скрещивающихся прямых существует плоскость, которой они обе параллельны.

Две плоскости параллельны, если они параллельны одной и той же прямой.

Если прямая параллельна одной из двух параллельных плоскостей, то она параллельна и другой.

Задание: начертить чертеж к заданию и подтвердить свой выбор ответа на чертеже.

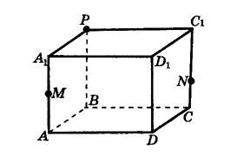
Если в параллелепипеде ABCDA₁B₁C₁D₁ точки М и К принадлежат ребрам ВВ₁ и CC₁ соответственно, то плоскости ABD и МКС пересекаются по прямой

Если в тетраэдре точки К и Е являются серединами ребер АВ и DC соответственно, то плоскости ADK и ЕСК пересекаются

1) в точке С 2) в точке D 3) по прямой КЕ 4) по прямой DK

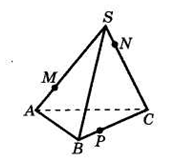
Если в тетраэдре DАВС точки F, N и G лежат на ребрах DB, DC и АС соответственно, то точка пересечения отрезков BN и CF лежит в плоскости

1) ABD 2) АВС 3) ABG 4) CDB

1) 30° 2) 45° 3) 60° 4) 90°

Если в тетраэдре DABC, точки К и Е принадлежат ребрам АВ и ВС соответственно, то скрещивающимися являются прямые

1) КЕ и АС 2) KE и BD 3) КЕ и АВ 4) КЕ и ВС

В основании параллелепипеда ABCDA₁B₁C₁D₁ лежит ромб ABCD. Если A₁D₁C₁ = 120°, то угол между прямыми A₁C₁ и ВС равен

1) 30° 2) 60° 3) 90° 4) 120°

Если в параллелепипеде точки К, Е и М – середины ребер AD, CC₁ и DD₁ соответственно, то сечением параллелепипеда ABCDA₁B₁C₁D₁ плоскостью ЕМК будет

1) треугольник 2) параллелограмм 3) трапеция 4) шестиугольник

П 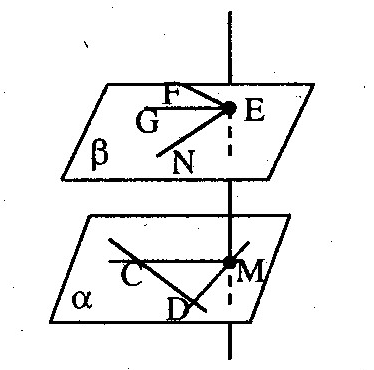лоскости  и  параллельны, прямая ЕМ пересекает , FE лежит в плоскости  и параллельна CD, GE параллельна CM, EN параллельна DM. Плоскость ЕМС пересекает плоскость  по прямой

1) GE 2) FE 3) EN 4) FN

В параллелепипеде ABCDA₁B₁C₁D₁ точки К и М середины ребер AD и CD соответственно. Линия пересечения плоскостей KCC₁ и АА₁М

2) параллельна DD₁

3) совпадает с ребром DD₁

Треугольник ABC и трапеция АВКР (АВ – основание) не лежат в одной плоскости. Каково расположение прямых РК и MN, если MN – средняя линия треугольника? Почему? (постройте чертеж и объясните свой ответ)

Задание: решить задачу с подробным описанием ее решения

Сумма длин всех рёбер параллелепипеда ABCDA₁B₁C₁D₁ равна 324 см. Известно, что AB : B₁C₁ : DD₁ = 2 : 3 : 4. Найдите периметр AA₁D₁D

Плоскость , параллельная стороне ВС треугольника АВС, пересекает стороны АВ и АС в точках Е и F соответственно, так, что AF : FC = 3 : 5. Отрезок ВС = 20 см, Найдите длину отрезка EF.

Плоскость  пересекает тетраэдр DABC в точках М, N и К так, что M  DA, N  DB и K  DC. Известно, что DM : MA = DN : NB = DK : KC = 2 : 1. Найдите отношение периметра треугольника ABC к периметру треугольника MNK

Построить сечения многогранника через заданные элементы:

Итоговая проверочная работа

Аксиомы стереометрии, параллельность прямых и плоскостей

Определите, верно ли утверждение:

Если две прямые параллельны третьей прямой, то они параллельны.

Две плоскости параллельны, если некоторая прямая, лежащая в одной плоскости, параллельна другой плоскости.

Если через прямую можно провести две плоскости, параллельные второй прямой, то эти прямые пересекаются.

Две плоскости параллельны, если они параллельны одной и той же третьей плоскости.

Задание: начертить чертеж к заданию и подтвердить свой выбор ответа на чертеже.

Если в параллелепипеде ABCDA₁B₁C₁D₁ точки М и К принадлежат ребрам ВВ₁ и CC₁ соответственно, то плоскости КМВ и A₁D₁C₁ пересекаются по прямой

Если в тетраэдре точки К и Е являются серединами ребер АВ и DC соответственно, то плоскости КСЕ и АВС пересекаются

1) по прямой КС 2) по прямой АС 3) в точке С 4) в точке Е

Если в тетраэдре DАВС точки F, N и G лежат на ребрах АB, АD и АС соответственно, то точка пересечения отрезков BN и DF лежит в плоскости

1) CDG 2) ACD 3) ABD 4) ABG

1) 30° 2) 45° 3) 60° 4) 90°

Если в тетраэдре DABC, точки К и Е принадлежат ребрам CD и ВD соответственно, то скрещивающимися являются прямые

1) КЕ и CD 2) KE и BC 3) КЕ и DВ 4) КЕ и AС

В основании параллелепипеда ABCDA₁B₁C₁D₁ лежит ромб ABCD. Если ADC = 140°, то угол между прямыми B₁D₁ и AD равен

1) 40° 2) 70° 3) 110° 4) 140°

Если в параллелепипеде точки К и Е – середины ребер AD и DC соответственно, точка М делит ребро А₁D₁ в отношении 2 : 1, считая от А₁, то сечением параллелепипеда ABCDA₁B₁C₁D₁ плоскостью ЕМК будет

1) треугольник 2) параллелограмм 3) трапеция 4) шестиугольник

П лоскости  и  параллельны, прямая ЕМ пересекает , FE лежит в плоскости  и параллельна CD, GE параллельна CM, EN параллельна DM. Плоскость CED пересекает плоскость  по прямой

1) FE 2) FN 3) GE 4) EN

В параллелепипеде ABCDA₁B₁C₁D₁ точки К и М середины ребер DD₁ и D₁C₁ соответственно. Линия пересечения плоскостей KC₁B₁ и АDМ

Ромб ABCD и трапеция BCMN (ВС – основание) не лежат в одной плоскости. Как расположены прямые MN и AD? Почему? (постройте чертеж и объясните свой ответ)

Задание: решить задачу с подробным описанием ее решения

Сумма длин всех рёбер параллелепипеда ABCDA₁B₁C₁D₁ равна 432 см. Известно, что AB : B₁C₁ : DD₁ = 2 : 3 : 4. Найдите периметр AA₁D₁D

Плоскость , параллельная стороне AС треугольника АВС, пересекает стороны АВ и BС в точках Е и F соответственно, так, что AE : BE = 3 : 8. Отрезок EF = 12 см, Найдите длину отрезка AC.

Плоскость  пересекает тетраэдр DABC в точках М, N и К так, что M  AD, N  BD и K  CD. Известно, что DM : MA = DN : NB = DK : KC = 1 : 2. Найдите отношение периметра треугольника MNK к периметру треугольника ABC

Построить сечения многогранника через заданные элементы:

Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

2. Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми

Скрещивающиеся прямые

Нам известны два случая расположения прямых в пространстве a ∩ b; а || b. Общее для них: они лежат в одной плоскости (рис. 1, 2).

(по следствию из аксиомы)

(по определению параллельных прямых)

ЗАДАНИЕ №1 в рабочей тетради

Значит, в пространстве есть прямые, которые не пересекаются и не являются параллельными, так как они не лежат в одной плоскости. Такие прямые называются скрещивающимися.

Определение: Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Теорема (признак скрещивающихся прямых)

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

Дано: АВ ⊂ α, CD ∩ α = С, С ∉ АВ (рис. 4).

Доказать, что АВ скрещивается с CD.

Допустим, что CD и АВ лежит в одной плоскости. Пусть это будет плоскость β.

Плоскости совпадают, чего быть не может, так как прямая CD пересекает α. Плоскости, которой принадлежат АВ и CD не существует и следовательно по определению скрещивающихся прямых АВ скрещивается с CD.

ЗАДАНИЕ №2 в рабочей тетради

Теорема :

Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой плоскости, и притом только одна.

Доказательство: учащиеся разбирают по учебнику самостоятельно с последующей записью на доске и в тетрадях.

Дано: АВ скрещивается CD (рис. 6).

Построить α: АВ ⊂ α, CD || α.

Доказать, что α — единственная.

1. Через точку А проведем прямую АЕ, АЕ || CD.

2. Прямые АЕ и АВ пересекаются и образуют плоскость α. АВ ⊂ α (по построению), CD || α (по признаку параллельности прямой и плоскости), α — искомая плоскость.

3. Докажем, что α — единственная плоскость. α — единственная по следствию из аксиом. Любая другая плоскость, которой принадлежит АВ, пересекает АЕ и, следовательно, прямую CD.

В доказательстве этой теоремы дается способ построения плоскости, проходящей через данную точку и параллельной двум скрещивающимся прямым. Рассмотреть задачу на построение.

Задание №3-№4 в рабочей тетради

Углы с сонаправленными сторонами. Угол между прямыми

Любая прямая а, лежащая в плоскости, разделяет плоскость на 2 части, называемые полуплоскостями. Прямая а называется границей каждой из этих полуплоскостей.