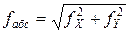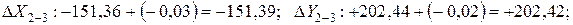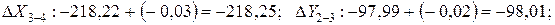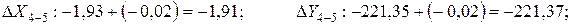Дирекционный угол это один из углов ориентирования, который применяется в геодезии при ориентировании линий в зональной системе координат (проекция Гаусса-Крюгера).
Дирекционный угол определяют по топографической карте или плану, или вычисляют аналитически, вначале определив азимут линии и угол сближения меридианов. На местности дирекционный угол измерить невозможно.
Дирекционный угол отсчитывается от северного направления осевого меридиана шестиградусной зоны (или параллельного ему направления) по ходу движения часовой стрелки от 0° до 360° и обозначается буквой α.
На рисунке показан дирекционный угол линии BC в одной из шестиградусных зон проекции Гаусса-Крюгера.
Следует ещё раз обратить внимание, что дирекционный угол, в отличие от азимутов, отсчитывается не от географического или магнитного меридианов, а от осевого меридиана зональной системы координат.
На рисунке для линии BC показаны её дирекционный угол αB-C и азимут AB-C. Из рисунка видно, что зная истинный азимут и угол сближения меридианов γ, дирекционный угол линии можно вычислить по формуле:
где γ – угол сближения меридианов со своим знаком.
Пример вычисления дирекционного угла линии по азимуту:
вычислить дирекционный угол линии 1-2, если ее истинный азимут равен А1-2 = 15°25′, а угол сближения меридианов γ = -0°02′.
согласно формулы можем записать
Также, по известному дирекционному углу линии и углу сближения меридианов, можно вычислить истинный азимут линии:
где γ – угол сближения меридианов со своим знаком.
Пример вычисления азимута линии по её дирекционному углу:
вычислить истинный азимут линии 3-4, если ее дирекционный угол равен α3-4 = 214°11′, а угол сближения меридианов γ = -0°03′.
согласно с формулой запишем
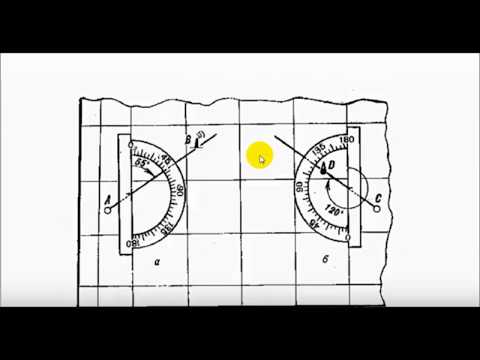
Для определения дирекционного угла по топографической карте или плану, используют координатную сетку (километровую сетку), для чего транспортир прикладывают к координатной линии как показано на рисунке.
Использование дирекционных углов упрощает расчеты – при вычислениях не требуется постоянно учитывать угол сближения меридианов как при ориентировании линий с помощью азимутов.
Видео:Топография. Как найти дирекционный угол на карте. Контрольно проверочные занятия. КПЗ.Скачать
Дирекционный угол
Дирекционный угол (α) – это угол между проходящими через данную точку направлением на ориентир и линией параллельной оси абсцисс, отчитываемой от северного направления оси абсцисс по ходу часовой стрелки оси 0 до 360°.
Дирекционные углы направлений измеряются преимущественно по карте или определяются по магнитным азимутам.
Дирекционный угол ориентирного направления может определяться геодезическим или гироскопическим способом, из астрономических наблюдений, с помощью магнитной стрелки буссоли и по контурным точкам карты (аэрофотоснимка).
При геодезическом способе ориентирования дирекционный угол ориентирного направления может быть получен непосредственно из каталога (списка) координат, решением обратной геодезической задачи по координатам геодезических пунктов, при выполнении засечек или прокладке полигонометрического хода одновременно с определением координат привязываемых точек, а также путем передачи угловым ходом от направления с известным дирекционным углом.
При гироскопическом способе ориентирования с помощью гирокомпаса определяют истинный (астрономический) азимут ориентирного направления, а затем переходят к дирекционному углу этого направления. Азимут ориентирного направления с помощью гирокомпаса определяется по двум, трем (четырем) точкам реверсии. Увеличение числа точек реверсии до трех (четырех) обеспечивает контроль и повышает точность определения дирекционного угла.
При астрономическом способе ориентирования дирекционный угол ориентирного направления определяют путем перехода от азимута светила к азимуту ориентирного направления, а от последнего — к дирекционному углу. Азимут светила вычисляют по результатам наблюдений, выполненных на местности с данной точки. Азимут ориентирного направления из астрономических наблюдений может быть получен и с помощью азимутальной насадки АНБ-1 к буссоли ПАБ-2А непосредственно на местности без выполнения вычислений.
Способ определения дирекционного угла ориентирного направления из астрономических наблюдений является наиболее точным.
Работы в поле при этом способе заключаются в измерении горизонтального угла Q между направлением на светило и заданным направлением в момент времени наведения прибора на светило. По моменту времени наблюдения светила вычисляют азимут а светила, от него переходят к астрономическому азимуту А направления на ориентир: A’ = a + Q. Зная значение сближения меридианов у в точке наблюдения, определяют дирекционный угол с ориентирного направления: a = A — y.
При определении дирекционного угла ориентирного направления с помощью магнитной стрелки буссоли на местности сначала получают магнитный азимут ориентирного направления, а затем, учитывая поправку буссоли, переходят к дирекционному углу. Дирекционный угол ориентирного направления определяется по формуле: а = Ат + (±dАт).
По карте (аэрофотоснимку) дирекционный угол ориентирного направления получают решением обратной геодезической задачи по координатам двух контурных точек Координаты контурных точек при этом определяются по карте (аэрофотоснимку) с помощью циркуля измерителя и поперечного масштаба. Точность полученного дирекционного угла будет тем выше, чем больше расстояние между начальной и ориентирной точками и чем точнее определены координаты этих точек.
Дирекционный угол по карте также можно определить с помощью хордоугломера. Для этого опознают на карте исходную и ориентирную точки, проводят через них прямую линию и получают на карте ориентирное направление. Измерив с помощью хордоугломера угол между северным направлением вертикальной линии километровой сетки карты и ориентирным направлением, получают дирекционный угол этого направления.
Свойства дирекционных углов: дирекционные углы α1=α2=α3 так как параллельные линии пересекаются одной линией. Следовательно, углы равны.
Рисунок 2. — Дирекционные углы.
Дирекционные углы могут быть прямыми и обратными (они отличаются на 180°):
Рисунок 3. — Прямые и обратные дирекционные углы.
В зависимости от выбора системы поверхностных координат или проекции земного эллипсоида на плоскость дирекционный угол может иметь собственное название. Например, геодезическийдирекционный угол, гауссов дирекционный угол и т.д.
Видео:Азимут магнитный. Дирекционный угол. Как их определить на карте. Гринвичский меридиан.Скачать

Вычисление дирекционных углов
По известному дирекционному углу an и по исправленным горизонтальным углам bиспр вычисляются дирекционные углы остальных сторон теодолитного хода по формулам для правых горизонтальных углов:
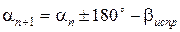
Величина дирекционного угла не может превышать 360° и быть меньше 0°. Если величина дирекционного угла больше 360°, то из результата вычислений необходимо вычесть 360° (см. пример).
Контроль вычисления дирекционных углов. В замкнутом теодолитном ходе в результате вычислений получается дирекционный угол исходной стороны.
Пример вычисления дирекционных углов:
Дирекционный угол исходной стороны a1-2 равен 45°45¢.
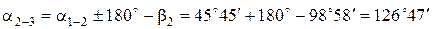
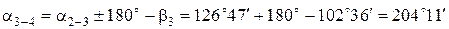
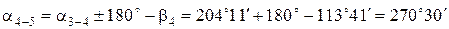
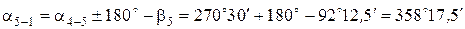
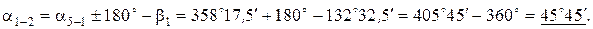
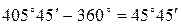
Контроль вычисления дирекционных углов получился.
Все результаты вычислений заносятся в таблицу «Ведомость вычисления координат» (табл. 2).
1.3 Вычисление приращений координат
Вычисление приращений координат выполняется по формулам:
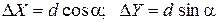
где d – горизонтальное проложение (длина) линии; a – дирекционный угол этой линии.
Приращения координат вычисляются с точностью два знака после запятой.
Пример вычисления приращений координат:
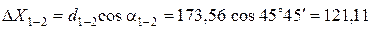
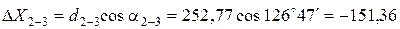
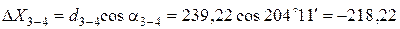
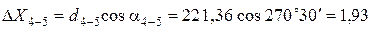
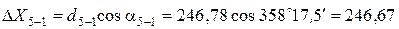
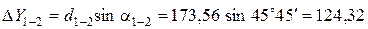
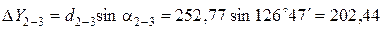
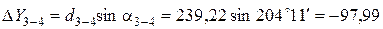
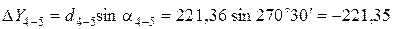
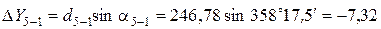
Все результаты вычисления заносятся в табл. 2. Пример вычисления тригонометрических функций на калькуляторе приведен в отдельном файле.
1.4 Уравнивание линейных измерений
Разность между суммой вычисленных приращений координат и теоретической суммой называется линейной невязкой хода и обозначается fХ и fY. Уравнивание линейных измерений выполняется по осям Х и Y.
Линейная невязка вычисляется по формулам:
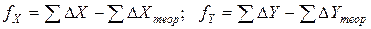
Теоретическая сумма приращений координат зависит от геометрии хода. В замкнутом теодолитном ходе она равна нулю, тогда невязка равна
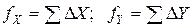
Прежде, чем распределять невязки в приращения координат, необходимо убедиться в их допустимости. Для чего вычисляется абсолютная невязка хода fабс
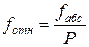
где Р – периметр хода (сумма длин сторон), м.
Относительная невязка сравнивается с допустимой 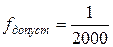
В случае, когда полученная относительная невязка допустима, т.е. 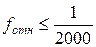
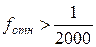
Поправки в приращения координат dX и dY вычисляются по формулам с округлением до 0,01 м:
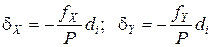
где dX и dY – поправка в приращение по оси Х и Y, соответственно, м; fX и fY – невязки по осям, м; Р – периметр (сумма сторон), м; di – измеренная длина (горизонтальное проложение), м.
Знак у поправки противоположен знаку невязки. Поправки записываются в «Ведомость вычисления координат». В примере (табл. 6) поправки показаны красным цветом.
После вычисления поправок следует сделать проверку, т.е. сложить все поправки. Если их сумма будет равна невязке с обратным знаком, то распределение невязки выполнено правильно. То есть:
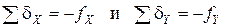
Вычисляются исправленные приращения.
Полученные поправки алгебраически прибавляются к соответствующим приращениям и получаются исправленные приращения:
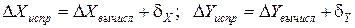
Контроль: сумма исправленных приращений в замкнутом теодолитном ходе должна равняться нулю, т.е. должно выполняться равенство:
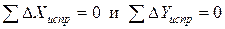
Пример вычисления линейной невязки:
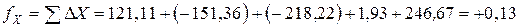
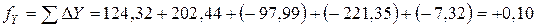
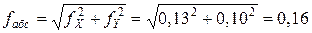
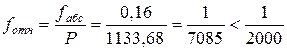
Пример вычисления поправок в приращения координат:
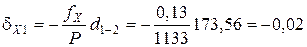
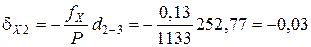
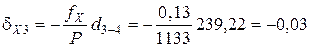
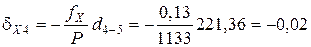
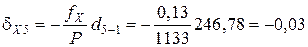
Контроль 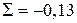
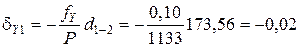
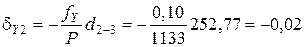
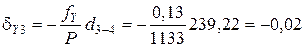
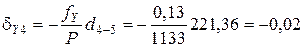
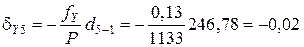
Контроль 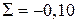
Поправки записываются в «Ведомость вычисления координат» над вычисленными приращениями. В примере поправки показаны красным цветом (Табл. 2).
Пример вычисления исправленных приращений координат:
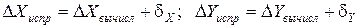
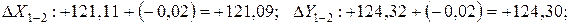
Контроль 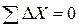
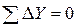
Сумма исправленных приращений равна нулю, т.е. контроль выполняется.
🔍 Видео
Дирекционный угол поправка направления магнитный азимут военная топографияСкачать

Азимут и Дирекционный УголСкачать

Ориентирование линий. Дирекционный угол. РумбСкачать

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

AlpineQuest и OfflineMaps магнитный азимут и дирекционный уголСкачать
Дирекционный угол , Истинный азимут, Магнитный азимут,Румб. (геодезия) (4 задание)Скачать

Внешний угол треугольникаСкачать

Измерение и нанесение дирекционных углов на картеСкачать

Соотношение между дирекционным углом и румбом в геодезииСкачать

7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

3. Вычисление дирекционных углов и румбов замкнутого теодолитного ходаСкачать

Как найти румб и дирекционный угол на карте двумя способами. Геодезия, работа с картой.Скачать

По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Измерение угла с помощью транспортираСкачать

Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Бусоль - дирекционный угол, магнитный азимут, поправка бусолиСкачать

Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

Высота, биссектриса, медиана. 7 класс.Скачать