В одной окружности проведены хорды ас и ве пересекающиеся

Геометрия | 5 — 9 классы

В одной окружности проведены хорды AC и BE, пересекающиеся в точке M.

Найдите длину отрезка AM если CM = 2, BM = 6, EM = 4.

AB и AC, причем AB = 2 см, AC = 1 см, РCAB = 120° .

. Прямые AB и CD пересекаются в точке М так, что AM = 2.

Видео:№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать

Из точки А, взятой на окружности, проведены диаметр АВ = 10 см и хорда АС Из точки В проведены к хорде перпендикуляр длиной 6 и касательнвя, пересекающая продолжение хорды в точке Д?

Из точки А, взятой на окружности, проведены диаметр АВ = 10 см и хорда АС Из точки В проведены к хорде перпендикуляр длиной 6 и касательнвя, пересекающая продолжение хорды в точке Д.

Найти длину касательной.

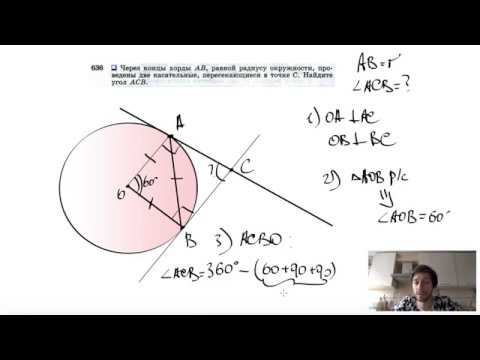
Видео:№636. Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающиесяСкачать

В окружности проведены две пересекающиеся хорды?

В окружности проведены две пересекающиеся хорды.

Одна из них делиться на отрезки 3 см и 12 см, а другая пополам.

Найдите длину второй хорды.

Видео:Геометрия В окружности проведены хорды AB и CD, пересекающиеся в точке M. Дано: AM/МВ =5/7Скачать

Две хорды одной окружности пересекаются в точке делящей одну хорду на отрезки 2 см и 16 см а другую на отрезки один из которых в 2 раза больше другого найдите длину второй хорды?

Две хорды одной окружности пересекаются в точке делящей одну хорду на отрезки 2 см и 16 см а другую на отрезки один из которых в 2 раза больше другого найдите длину второй хорды.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

В окружности проведены три попарно пересекающиеся хорды равной длины?

В окружности проведены три попарно пересекающиеся хорды равной длины.

Каждая хорда разделена точками пересечения на три части равной длины.

Найти радиус окружности, если длина каждой из хорд равна а.

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

В окружности проведены две пересекающиеся хорды?

В окружности проведены две пересекающиеся хорды.

Одна из них делится на отрезки 2 см и 6 см, а длина другой хорды 7 см.

Найдите отрезки второй хорды.

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Радиус окружности равен 11см?

Радиус окружности равен 11см.

Удаленную от центра окружности на 7см, проведена хорда длиной 18см.

Найдите отрезки, на которые точка А делит данную хорду.

(желательно с рис).

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

К окружности с диаметром АС проведена касательная ВС?

К окружности с диаметром АС проведена касательная ВС.

Отрезок АВ пересекает окружность в точке D.

Через точку D проведена еще одна касательная к окружности, пересекающая отрезок ВС в точке К.

Найдите длину отрезка СК, если ВС = 6.

Видео:№672. Через точку А, лежащую вне окружности, проведены две секущие, одна из которых пересекаетСкачать

В окружности проведены две пересекающиеся хорды?

В окружности проведены две пересекающиеся хорды.

Одна из них делится на отрезки 3см и 12см, а другая — пополам.

Найдите длину второй хорды.

Видео:Хорды AC и BD окружности пересекаются в точке P, BP=6, CP=8, DP=12. Найдите AP.Скачать

В одной окружности проведены хорды AD и BF, пересекающиеся в точке К?

В одной окружности проведены хорды AD и BF, пересекающиеся в точке К.

Найдите длину отрезка ВК, если АК = 8, DK = 3, FK = 4.

Видео:Геометрия В окружности проведены две хорды AB = a и AC = b. длина дуги AC вдвое больше длины дуги ABСкачать

Две равные окружности пересекаются в точках А и В?

Две равные окружности пересекаются в точках А и В.

Через точку А проведена хорда АМ одной окружности, а через точку В — хорда ВN другой окружности, причем АМ и BN параллельны.

Доказать, что эти хорды равны.

Вы зашли на страницу вопроса В одной окружности проведены хорды AC и BE, пересекающиеся в точке M?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

Ответ : |BC| = a = 2√3. |2AO + 2CO| = 4. |AС — (3 / 2) * ОС| = 3. Объяснение : В равностороннем треугольнике центр описанной окружности лежит на пересечении высот треугольника, которые являются и биссектрисами и медианами. АО — радиус описанной о..

Привет, BD — выстота = >BDC = 90° найдем угол DBC = 180 — (90 + 42) = 48° Треугольники авd и abd равны = >ABD = 48 ABC = 48 + 48 = 96°.

Пусть A1 — начало координат Ось X — A1B Ось Y — A1D1 Ось Z — A1A A1D1 (0 ; 1 ; 0) M(1 ; 1 ; 0. 5) D(0 ; 1 ; 1) Уравнение A1MD ax + by + cz = 0 подставляем координаты точек a + b + 0. 5c = 0 b + c = 0 Пусть с = — 2 тогда b = 2 a = — 1 — x + 2y — 2z ..

Р = а + в + с (68 — 16) : 2 = 26(см) боковая сторона треугольника.

68 — 16 = 52приходится на две стороны, так как треугольник равнобедренный то стороны равные 52 : 2 = 26 боковая сторона.

36 : 2 = 18 — отрезок КВ 18 : 2 = 9 — отрезок МК.

1) Точки в пл. АДД1 : А , Д Д1 , А1 . Точки в пл. АВС : А , В , С , Д . 2) MS лежит в пл. АВСД МД в пл. АВСД и АА1Д1Д АВ в пл. АВСД и АА1В1В 3) АА1 , ВВ1 , СС1 , ДД1 перпендикулярны пл. АВСД 4) прямой АД параллельны пл. ВВ1С1С и А1В1С1Д1 5) ..

1)Угол 1 = 65, 2)180 — 65 = 115(угол 2) 3)180 — 115 = 65 градусов (угол 3) Эх, вернуться бы в 7 класс.

Пусть B начало координат Ось X — BA Ось Y — BC Ось Z — BB1 направляющий вектор BD (1 ; 0 ; 1) направляющий вектор DA1 (0 ; — 1 ; 1) Длина√2 | i j k | | 1 0 1| = i | 0 1| + j |1 1 | + k | 1 0 | | 0 — 1 1| | — 1 1| |0 1| | 0 — 1 | Длина√3 Расстояние√3 ..

В градусе 60 минут, значит 5°48′ + 7°35′ = 13°83′ = 14°23′ 32°17′ + 8°45′ = 40°62′ = 41°02′.

Видео:№662 (исправлено) Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если ∪AD=54°Скачать

В одной окружности проведены хорды ас и ве пересекающиеся

В окружности проведены хорды АС и ВD, пересекающиеся в точке О, причем касательная к окружности, проходящая через точку С, параллельна ВD.

а) Докажите, что DC 2 = АС ∙ СО.

б) Найдите площадь треугольника СDО, если известно, что AB : ВО = 3 : 1, а площадь треугольника АСD равна 36.

а) Проведем диаметр окружности CK. Он будет перпендикулярным к заданной касательной, к которой параллельна хорда BD. Отсюда получим: BD ⊥ CK.

Рассмотрим четырехугольник ABCD. Отрезок диаметра, принадлежащий ΔBD окажется его высотой и медианой, откуда: ΔBCD — равнобедренный, то есть BC = DC, ∪BmC = ∪DnC.

В ΔCOD и ΔACD: ∠ACD — общий, ∠CDB = ∠CAD как вписанные, опирающиеся на равные дуги BmC и DnC соответственно. Значит, Δ COD

что и требовалось доказать,

б) В треугольниках ABO и CDO ∠ABD = ∠ACD как вписанные углы, опирающиеся на одну и ту же дугу AKD, ∠BAC = ∠CDB как вписанные углы опирающиеся на дугу BmC. Следовательно, ΔABO

Но значит, Выше было получено: Тогда:

Треугольники ACD и CDO имеют равные высоты, проводимые к сторонам AC и CO соответственно. Тогда:

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б.	3
Получен обоснованный ответ в пункте б. Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки.	2
Имеется верное доказательство утверждения пункта а. При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. Видео:№635. Через точку А окружности проведены касательная и хорда, равная радиусу окружности.Скачать В одной окружности проведены хорды ас и ве пересекающиеся Вопрос по геометрии: В одной окружности проведены хорды AC и BE,пересекающиеся в точке M. Найдите длину отрезка AM если CM=2,BM=6,EM=4 Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ? Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно! Ответы и объяснения 1 AB и AC, причем AB = 2 см, AC = 1 см, РCAB = 120° . . Прямые AB и CD пересекаются в точке М так, что AM= 2. Знаете ответ? Поделитесь им! Как написать хороший ответ? Чтобы добавить хороший ответ необходимо: Отвечать достоверно на те вопросы, на которые знаете правильный ответ; Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему; Писать без грамматических, орфографических и пунктуационных ошибок. Этого делать не стоит: Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения; Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее; Использовать мат — это неуважительно по отношению к пользователям; Писать в ВЕРХНЕМ РЕГИСТРЕ. Есть сомнения? Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия. Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы! Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения. 🎦 Видео №645. Из концов диаметра АВ данной окружности проведены перпендикуляры АА1 и ВВ1 к касательнойСкачать Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать Через точку A, лежащую вне окружности, проведены две прямые.Скачать ОГЭ по математике 2024 геометрия | Разбор всех 16 заданийСкачать №667. Диаметр АА1 окружности перпендикулярен к хорде ВВ1 и пересекает ее в точке С. Найдите BB1Скачать Геометрия В окружности с центром O проведены диаметр AB и хорда AC. Докажите, что угол BOC = 2 угламСкачать ✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать Задание 24 Свойство пересекающихся хордСкачать Поделиться или сохранить к себе: Смотрите также Ящик тянут по земле по горизонтальной окружности длиной 60 Ящик тянут по земле по горизонтальной окружности длиной 40 Ящик тянут по земле по горизонтальной окружности диаметром 20 Ящик тянут по земле за веревку по горизонтальной окружности длиной Ящик тянут по земле за веревку по горизонтальной окружности диаметром Электрон равномерно движется по окружности в однородном магнитном поле Электрон и протон ускоренные разностью потенциалов движутся по окружности Шарик скатывается по желобу изогнутому в виде дуги окружности