Из концов диаметра в окружности опущены перпендикуляры

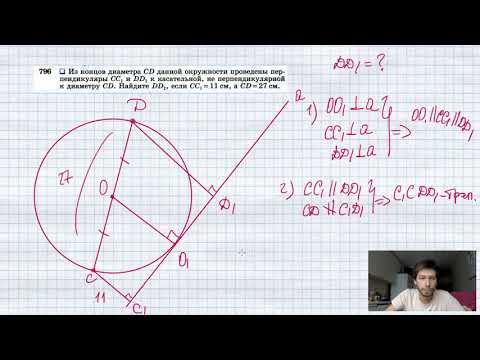
Видео:№796. Из концов диаметра CD данной окружности проведены перпендикуляры СС1 и DD1 к касательнойСкачать

Задача

Даны окружность с центром О и точка А вне окружности. а) Проведен диаметр окружности. Пользуясь только линейкой*, опустите перпендикуляр из точки А на этот диаметр. б) Через точку А проведена прямая, не имеющая общих точек с окружностью. Пользуясь только линейкой, опустите перпендикуляр из точки О на эту прямую.

*Примечание. Под «линейкой» в задачах на построение всегда подразумевается не измерительный инструмент, а геометрический — с его помощью можно только проводить прямые (через две имеющиеся точки), но не измерять расстояние между точками. Кроме того, геометрическая линейка считается односторонней — с ее помощью нельзя провести параллельную прямую, просто приложив одну сторону линейки к двум точкам и проведя линию вдоль другой стороны.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Подсказка 1

Используйте концы диаметра, а не центр окружности.

Видео:Окружность. 7 класс.Скачать

Подсказка 2

Угол с вершиной на окружности, опирающийся на ее диаметр, — прямой. Зная это, вы можете построить две высоты в треугольнике, образованном концами диаметра и точкой А.

Видео:КАК НАЙТИ ДИАМЕТР ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Подсказка 3

Попробуйте решить сначала более простой случай, чем заданный в пункте б), — когда данная прямая пересекает окружность.

Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Решение

а) Пусть ВС — данный диаметр (рис. 1). Для решения задачи просто вспомним первые две подсказки: если провести прямые AВ и АC, а затем соединить точки их пересечения с окружностью с нужными вершинами треугольника ABC, то получатся две высоты этого треугольника. А так как высоты треугольника пересекаются в одной точке, то прямая CH будет третьей высотой, то есть искомым перпендикуляром из А к диаметру ВС.

б) Решение этого пункта, однако, даже в том случае, который дан в третьей подсказке, не кажется более простым: да, мы можем провести диаметры, соединить их концы и получить прямоугольник ABCD (рис. 2, на котором, для простоты, точка А отмечена на окружности), но как это приближает нас к построению перпендикуляра из центра окружности?

А вот как: так как треугольник AOB равнобедренный, то перпендикуляр (высота) OK пройдет через середину K стороны AB. А значит, задача свелась к нахождению середины этой стороны. Как ни удивительно, но окружность больше нам совсем не нужна, да и точка D тоже, в общем, «лишняя». А вот отрезок CD — не лишний, но на нем нам потребуется не какая-то конкретная точка, а совершенно произвольная точка E! Если обозначить за L точку пересечения BE и AC (рис. 3), а затем продлить AE до пересечения с продолжением BC в точке M, то прямая LM — это решение всех наших забот и проблем!

Правда, очень похоже, что LM пересекает AB посередине? Это и правда так. Попробуйте доказать это. Мы же отложим доказательство до конца решения задачи.

Итак, мы научились находить середину отрезка AB, а значит, научились опускать перпендикуляр на AB из центра окружности. Но что делать с исходной задачей, в которой данная прямая не пересекает окружность, как на рис. 4?

Постараемся свести задачу к уже решенной. Это можно сделать, например, так.

Сначала построим прямую, симметричную данной относительно центра окружности. Построение понятно из рис. 5, на котором данная прямая — горизонтальная под окружностью, а построенная симметричная ей — выделена красным (две синие точки могут быть взяты на окружности совершенно произвольно). Заодно проведем через центр О еще одну прямую, перпендикулярную к одной из сторон получившегося в окружности прямоугольника, чтобы получить на данной прямой два равных по длине отрезка.

Имея две параллельные прямые, на одной из которых уже отмечены два конца и середина отрезка, возьмем произвольную точку T (например, на окружности) и построим такую точку S, что прямая TS будет параллельна имеющимся двум прямым. Это построение показано на рис. 6.

Тем самым мы получили хорду окружности, параллельную данной прямой, то есть свели задачу к решенной ранее версии, ведь к такой хорде проводить перпендикуляр из центра окружности мы уже умеем.

Осталось привести доказательство факта, который мы использовали выше.

Четырехугольник ABCE на рис. 3 — трапеция, L — точка пересечения ее диагоналей, а M — точка пересечения продолжений ее боковых сторон. По известному свойству трапеции (его еще называют замечательным свойством трапеции; здесь можно посмотреть, как оно доказывается) прямая ML проходит через середины оснований трапеции.

Собственно, еще раз мы фактически опирались на эту же теорему уже в последней подзадаче, когда проводили третью параллельную прямую.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Послесловие

Теория геометрических построений одной линейкой, когда задана вспомогательная окружность с центром, разработана замечательным немецким геометром XIX века Якобом Штейнером (правильнее произносить его фамилию Steiner как «Штайнер», но в отечественной литературе уже давно закрепилось написание с двумя «е»). О его математических достижениях мы уже однажды рассказывали в задаче «Короче, Склифосовский». В книге «Геометрические построения, выполняемые с помощью прямой линии и неподвижного круга» Штейнер доказал теорему, согласно которой любое построение, которое может быть выполнено с помощью циркуля и линейки, может быть выполнено и без циркуля, если задана всего одна окружность и отмечен ее центр. Доказательство Штейнера сводится к демонстрации возможности осуществления базовых построений, обычно выполняемых с помощью циркуля, — в частности, к проведению параллельных и перпендикулярных прямых. Наша задача, как легко видеть, является частным случаем этой демонстрации.

Впрочем, к некоторым задачам Штейнер привел не единственный способ решения. Приведем второй способ и мы.

Возьмем на данной прямой две произвольные точки A и B (рис. 7). Сначала строим перпендикуляр из A на (синюю) прямую BO — это фактически решение нашей первой задачи, потому что эта прямая содержит диаметр окружности; все соответствующие построения на рис. 7 выполнены синим цветом. Затем строим перпендикуляр из B на (зеленую) прямую AO — это точно такое же решение точно такой же задачи, построения выполнены зеленым цветом. Тем самым мы получили две высоты треугольника AOB. Третья высота этого треугольника проходит через центр O и точку пересечения двух других высот. Она и является искомым перпендикуляром к прямой AB.

Но и это еще не все. Несмотря на всю (относительную) простоту второго способа, он «избыточно длинный». Это означает, что существует другой способ построения, требующий меньшего числа операций (в задачах на построение каждая линия, проведенная циркулем или линейкой, считается как одна операция). Построения, требующие минимального среди известных количества операций, французский математик Эмиль Лемуан (Émile Lemoine, 1840–1912) назвал геометрографическими (см.: Geometrography).

Итак, вашему вниманию предлагается геометрографическое решение пункта б). Оно требует всего 10 шагов, при этом шесть первых — «естественные», а следующие три — «удивительные». Самый последний шаг, проведение перпендикуляра, пожалуй, тоже следует назвать естественным.

Мы хотим провести красный пунктирный перпендикуляр (рис. 8), для этого нам нужно отыскать на нем какую-нибудь точку, отличную от О. Поехали.

1) Пусть A — произвольная точка на прямой, а C — произвольная точка на окружности. Проводим прямую AC.

2)–3) Проводим диаметр OC (вторично пересекающий окружность в точке D) и прямую AD. Отмечаем вторые точки пересечения прямых AC и AD с окружностью — B и E, соответственно.

4)–6) Проводим BE, BD и CE. Прямые CD и BE пересеклись в точке H, а BD и CE — в точке G (рис. 9).

Кстати, а могло ли случиться так, что BE оказалось бы параллельно CD? Да, безусловно. В случае, когда диаметр CD перпендикулярен AO, то именно так и случается: BE и CD параллельны, а точки A, O и G лежат на одной прямой. Но возможность брать точку C произвольно предполагает наше умение выбрать ее так, чтобы CO и AO не были перпендикулярны!

И вот теперь обещанные удивительные шаги построения:

7) Проводим GH до пересечения с данной прямой в точке I.
8) Проводим CI до пересечения с окружностью в точке J.
9) Проводим BJ, которая пересекается с GH. где? Правильно, в красной точке, которая находится на вертикальном диаметре окружности (рис. 10).

10) Проводим вертикальный диаметр.

Вместо шага 8 можно было бы провести прямую DI, а затем на шаге 9 соединить вторую точку ее пересечения с окружностью с точкой E. Результат был бы той же самой красной точкой. Правда, это удивительно? Причем, даже неясно, что удивляет сильнее — то, что красная точка оказывается одной и той же для двух способов построения, или то, что она лежит на искомом перпендикуляре. Впрочем, геометрия — это ведь не «искусство факта», а «искусство доказательства». Так что постарайтесь доказать это.

Мелкая придирка не по существу:
> правильнее произносить его фамилию Steiner как «Штайнер», но в
> отечественной литературе уже давно закрепилось написание с двумя «е»

— ничего подобного. Так принято передавать немецкое -ei- для всех персон примерно до середины XX века. Причины этого не вполне понятны: фонетический переход -ei- в [-ai-] произошел за много веков до появления этой традиции транскрипции на русский
(в отличие, например, от перехода -ille- из [iλ] в [ij]: Марсель, Гильом — который произошел лишь в XIX веке, когда русская транскрипция уже устоялась).

Но по какой бы причине русская транскрипция с немецкого ни оказалась отстающей от реальной фонетики на много веков, она именно такова. Передавать Штейнера и прочих немцев XIX века через -ай- было бы анахронизмом. Не говоря уже о том, что Штейнер, помимо немецкой, еще и распространенная в России и других странах идишская фамилия, а их принято передавать через -ей- и по сей день.

А по существу вопрос: теорема гласит, что «любое построение, которое может быть выполнено с помощью циркуля и линейки, может быть выполнено и без циркуля, если задана всего одна окружность и отмечен ее центр».

Что имеется в виду под «если задана всего одна окружность»? Имеется ли в виду, что в задаче дана только одна окружность, и задание центра позволяет построить линейкой все то, что можно построить циркулем? Или имеется в виду, что берем любую задачу (скажем, деление отрезка пополам), и достаточно где-нибудь в произвольном месте задать окружность и ее центр, чтобы задача деления отрезка пополам решалась одной линейкой?

Да, имеется в виду ровно это. На плоскости чертежа задана произвольная окружность и ее центр. Это позволяет выполнить одной линейкой всё, что можно сделать циркулем и линейкой.

А деление отрезка пополам и так решается одной линейкой (без вспомогательной окружности). Вот одним циркулем — не решается.

> А деление отрезка пополам и так решается одной линейкой (без вспомогательной окружности

Допускаю, хотя не знаю такого способа.

> Вот одним циркулем — не решается.

Этого не может быть. По теореме Мора-Маскерони.

Этого противоречит вашим словам, будто линейкой можно построить середину отрезка.

Вот смотрите: если мы можем одной линейкой построить касательную к окружности из точки A, значит, возьмем две такие касательные. Проведем хорду, опирающуюся на две точки касания.

По вашим словам (выше), одной линейкой можно найти середину отрезка, а значит, и этой хорды.

Из исходной точки A через середину хорды проведем прямую. Это будет (продолженный) диаметр окружности.

Возьмем произвольную точку B и повторим с ней и той же окружностью то же самое. Получим второй диаметр.

Два диаметра дают нам центр окружности.

Итого получается, что если, как вы утверждаете, одной линейкой можно построить и касательную из заданной точки к заданной окружности, и середину заданного отрезка, то одной линейкой можно построить и центр данной окружности. Однако хорошо известно (доказано, по-моему, тем же Штейнером через сечения наклонного конуса), что это невозможно. А если б было возможно, то рассказанная вами теорема Штейнера-Понселе не имела бы смысла: получается, любое построение циркулем и линейкой можно было бы совершить просто линейкой безо всяких дополнительных условий (или точнее, требовалось бы иметь где-то окружность не обязательно с отмеченным центром).

Касательную одной линейкой точно можно построить, и это ничему не противоречит.

Что касается утверждения о построении середины отрезка, я хотел сказать вот что: для этого не нужно иметь вспомогательную окружность, достаточно иметь вспомогательную параллельную прямую.

Да, это тоже исследовано Штейнером. Он рассмотрел списки задач, разрешимых линейкой при следующих дополнительных условиях
а) дана одна параллельная прямая или отрезок, разделенный в известном рациональном отношении
б) даны две пары параллельных прямых, или два отрезка, деленные в рац. отношениях, или одна пара параллельных и один такой отрезок
в) дан вспомогательный квадрат

Все эти условия позволяют решать линейкой какой-то класс задач на построение, причем а) Ответить

Тогда и задача немного другая, и решение другое. Фактически в вашей задаче требуется построить квадрат по заданным противоположным вершинам (B и C).

PS. Насчет касательных. Да, конечно, построение не очень короткое — в сумме явно больше 15 линий получится. Через точку пересечения высот — экономнее

Видео:Доказательство того, что радиус перпендикулярен касательной | Окружность | ГеометрияСкачать

Из концов диаметра ав данной окружности

Видео:Свойство диаметра окружности. 7 класс.Скачать

Из концов диаметра АВ данной окружности проведены перпендикуляры АА1 и ВВ1 к касательной, которая не перпендикулярна к диаметру

Видео:ЕГЭ-2016. Математика. Задание 16 (планиметрия)Скачать

Ваш ответ

Видео:На окружности по разные стороны от диаметра AB ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

решение вопроса

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,890
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

Из концов диаметра АВ данной окружности проведены перпендикуляры АА1 и ВВ1 к касательной, которая не перпендикулярна к диаметру АВ?

Геометрия | 5 — 9 классы

Из концов диаметра АВ данной окружности проведены перпендикуляры АА1 и ВВ1 к касательной, которая не перпендикулярна к диаметру АВ.

Докажите, что точка касания является серединой отрезкаА1В1.

( Если можно, сделайте еще пожалуйста чертеж).

Пусть точка касания отрезкаА₁В₁ и окружностибудет М.

АА₁ и ВВ₁ перпендикулярны отрезку А₁В₁

ОМ — перпендикулярна А₁В₁ как радиус, проведенный в точку касания.

АА₁, ВВ₁ и ОМ параллельны.

АВВ₁А₁ — прямоугольная трапеция.

Точка О, как центр окружности, делит диаметр АВ пополам.

Т. К ОМ параллельна основаниям, ОМ — средняя линия трапеции.

Следовательно, М А₁ = МВ₁, что и требовалось доказать.

Видео:Окружность. Вебинар | МатематикаСкачать

Докажите, что диаметр, проведенный через середину хорды той же окружности, отличной от диаметра перпендикулярен этой хорде?

Докажите, что диаметр, проведенный через середину хорды той же окружности, отличной от диаметра перпендикулярен этой хорде.

Видео:Окружность. Как найти Радиус и ДиаметрСкачать

Докажите, что касательная к окружности перпендикулярна к радиусу этой окружности, проведенному в точку касания?

Докажите, что касательная к окружности перпендикулярна к радиусу этой окружности, проведенному в точку касания.

Видео:Планиметрия с окружностями | Задачи из ЕГЭ прошлых лет | №17 ЕГЭ по математикеСкачать

Две окружности имеют внешнее касание?

Две окружности имеют внешнее касание.

Докажите, что отрезок их внешней общей касательной , лежащий между точками касания , — среднее пропорциональное между диаметрами окружностей.

Видео:✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

Докажите что диаметр окружности перпендикулярный хорде проходит через ее середину?

Докажите что диаметр окружности перпендикулярный хорде проходит через ее середину.

Видео:РЕШЕНИЕ ЗАДАЧИ ПО ТЕМЕ «ОКРУЖНОСТЬ И КРУГ». Задачи | ГЕОМЕТРИЯ 7 классСкачать

Из концов диаметра AB окружности опущены перпендикуляры AA1 и BB1 на касательную?

Из концов диаметра AB окружности опущены перпендикуляры AA1 и BB1 на касательную.

Докажите, что точка касания С является серединой отрезка A1B1.

Видео:Длина окружности. Математика 6 класс.Скачать

К касательной EF окружности с центром в точке О из концов диаметра MN проведены два перпендикулярных отрезка ME и NF?

К касательной EF окружности с центром в точке О из концов диаметра MN проведены два перпендикулярных отрезка ME и NF.

Докажите, что точка касания P делит отрезок EF пополам.

Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Через концы диаметра AB окружности с центром О, проведены параллельные прямые, пересекающие окружность в точках М и К?

Через концы диаметра AB окружности с центром О, проведены параллельные прямые, пересекающие окружность в точках М и К.

Докажите, что МК — диаметр окружности.

Видео:Интенсив СИРОП по математике. Профильный ЕГЭ. Планиметрия. Задача 1Скачать

К касательной EF окружности с центром в точке О из концов диаметра MN проведены два перпендикулярных отрезка ME и NF?

К касательной EF окружности с центром в точке О из концов диаметра MN проведены два перпендикулярных отрезка ME и NF.

Докажите, что точка касания Р делит отрезок EF пополам.

Докажите : Касательная к окружности перпендикуляра радиусу, проведенному в точку касания?

Докажите : Касательная к окружности перпендикуляра радиусу, проведенному в точку касания.

Докажите, что перпендикуляр к касательной в точке касания проходит через центр окружности?

Докажите, что перпендикуляр к касательной в точке касания проходит через центр окружности.

Перед вами страница с вопросом Из концов диаметра АВ данной окружности проведены перпендикуляры АА1 и ВВ1 к касательной, которая не перпендикулярна к диаметру АВ?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

По теореме косинусов AC ^ 2 = AB ^ 2 + BC ^ 2 — 2 * AB * BC * cosB cosB = (AB ^ 2 + BC ^ 2 — AC ^ 2) / 2 * AB * BC = (25 + 49 — 81) / 2 * 5 * 7 = — 1 / 10.

Треугольник DBC — равнобедренный, так как у ромба все стороны равны. В равнобедренном треугольнике углы при основании равны, т. Е. DBC = CBD = (180° — 72°) / 2 = 54°.

СМОТРИ РЕШЕНИЕ НА РИСУНКЕ.

Ответы 2 и 3 правильные. Это треугольники которые равные по сторонам и углу между ними.

4, 3 + 5 = 9, 3 это лего просто плюс.

1. 4, 3 * 5 = 21, 5 2. 4, 3 + 21, 5 = 25, 8.

Во второй задаче можно рассмотреть треугольник как половину квадрата, разрезанного по диагонали. Тогда все становится очевидно, если конечно угол С там таки прямой. ))).

Ну ты скажи пример мы решим.

Радиус основания конуса равен 5 см, а периметр его осевого сечения равен 36 см. Найти объем конуса. Решение в приложении.

Касательная к окружности

О чем эта статья:

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

Из концов диаметра AB окружности опущены перпендикуляры АА1 и ВВ1 на касательную?

Геометрия | 5 — 9 классы

Из концов диаметра AB окружности опущены перпендикуляры АА1 и ВВ1 на касательную.

Доказать, что точка касания С является серединой отрезка А1В1.

Из центра О окружноси проведем радиус ОК в точку касания К.

«Радиус проведенный в точку касания — перпендикулярен касотельной», следовательно имеем 3 перпендикуляра к одной прямой, а по теореме они параллельны между собой.

Cледовательно АА1В1В — трапеция, а так как О — середина АВ, то ОК — средняя линия этой трапеции и значит точка К — серединаА1В1.

Наименьшее расстояние от данной точки до окружности равно 72 см, наибольшее — 98см?

Наименьшее расстояние от данной точки до окружности равно 72 см, наибольшее — 98см.

Из этой точки к окружности проведена касательная.

Найдите длину отрезка этой касательной до точки касания.

1. Из точки C вне окружности проведена к окружности касательная CA, где A точка касания CA = 20?

1. Из точки C вне окружности проведена к окружности касательная CA, где A точка касания CA = 20.

Через центр окружности и точку C проведена прямая, а к ней из точки A — перпендикуляр AB равный 12.

Найти радиус окружности 2.

В окружности радиуса из одного конца диаметра проведена касательная, а из другого — хорда, стягивающая дугу в Хорда продолжена до пересечения с касательной.

Найти внешний отрезок секущей.

45 баллов за ответ?

45 баллов за ответ!

Через точку С окружности с центром О провели касательную к этой окружности, AB — диаметр окружности.

Из точки А на касательную опущен перпендикуляр AD.

Докажите, что луч AC — биссектриса угла BAD.

N диаметров делят окружность на равные дуги?

N диаметров делят окружность на равные дуги.

Доказать что основания перпендикуляров , опущенных из произвольной точки М внутри окружности на эти диаметры, являются вершинами правильного многоугольника.

1) из точки О, являющейся центром окружности, на хорду СЕ опущен перпендикуляр ОМ?

1) из точки О, являющейся центром окружности, на хорду СЕ опущен перпендикуляр ОМ.

Докажите, что точка М является серединой хорды.

2)Проведите в окружности 2 диаметра MN и DF.

Докажите, что хорды MD и NF равны.

3)Дано : О — центр окружности, АВ = DC Доказать : угол АОВ = углу DOC.

Докажите , что диаметр окружности, проведенный через середину хорды(не является диаметром), перпендикулярен этой хорде?

Докажите , что диаметр окружности, проведенный через середину хорды(не является диаметром), перпендикулярен этой хорде.

Из точки окружности на диаметр проведён перпендикуляр 12см который делит его на отрезки?

Из точки окружности на диаметр проведён перпендикуляр 12см который делит его на отрезки.

Разность этих отрезков равна 18см.

Найти диаметр окружности.

Касательные проведенные из точки А к окружности радиуса 10 перпендикулярны?

Касательные проведенные из точки А к окружности радиуса 10 перпендикулярны.

Определите отрезки этих касательных ограниченные данной точкой и точками касания.

Отрезки АВ и АС являются отрезками касательных к окражности с центром О, проведенными из точки А?

Отрезки АВ и АС являются отрезками касательных к окражности с центром О, проведенными из точки А.

Найдите угол ВАС, если середина отрезка АО лежит на окружности.

Из точки, кратчайшее расстояние которой до окружности равно 25 мм, проведина к окружности касательная?

Из точки, кратчайшее расстояние которой до окружности равно 25 мм, проведина к окружности касательная.

Отрезок этой касательной между данной точки и точки касания равна 35 мм.

Найти длину диаметра окружности .

На этой странице находится вопрос Из концов диаметра AB окружности опущены перпендикуляры АА1 и ВВ1 на касательную?. Здесь же – ответы на него, и похожие вопросы в категории Геометрия, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 5 — 9 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.

1) Пусть ABCD — трапеция, AD║AC — основания, ∠A = 85°, ∠D = 5°, K, L, M, N — середины сторон, KL = 11, NM = 1. 2) Продолжим стороны AB и CD до пересечения в точке Е. ΔAED — прямоугольный, так как∠Е = 180° — (85° + 5°) = 180° — 90° = 90°. ЕМ — меди..

Пусть дана трапеция АВСД, где КЕ = 1 середина ВС и МР = 11 середина боковых сторон АВ и СД. Продолжим боковые стороны до пересечения в точке Т, тогда угол АТД = 90 градусам. Обозначим половину ВС через х , а половину АД чрез у, тогда получим систем..

Вы можете конкретно написать задание? 1и2 это углы? Тем более как они могут иметь уголы если они параллельны? Есть ли секущая с? Без нее никак.

30 + 90 = 120° это угол один 90 — 30 = 60° это угол четыре или три.

Смотри рисунок, обозначения понятны. Из треуг. ДЕС ДС / sinα = a / sin60 ДC = а * sinα / sin60 из треуг КВД ВД / sin(180 — (α + 60)) = a / sin60 ВД = а * sin(α + 60) / sin60 AB = BC = ДС + ВД = а * sinα / sin60 + а * sin(α + 60) / sin60 = а * (2sin..

P = 2 * 2 + 6 = 10 Периметр равен 10см.

Ответ : 3 Этот треугольник равнобедренный, и если провести высоту — треугольник разделится на 2 равных прямоугольных треугольника. Гипотенуза треугольников будет 3, а катет окажется 3, 5. Катеты прямоугольных треугольников всегда меньше гипотенузы.

Длина суммы векторов AO и BO равна стороне AD. Ответ 91.

R = S / p S — площадь ромба, p — его полупериметр (p = 2a, где a — сторона ромба). R = 24 / 12 = 2 p = 6 * 2 = 12.

Если площадь 24 то ее стороны равны 6 соответсвенно. Радиус может быть половина ее диагонали.