Нормальные и тангенциальные составляющие векторов поля

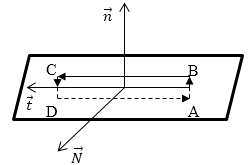
Привяжем прямоугольную систему координат к полю дефекта, направив ось z перпендикулярно поверхности ферромагнетика по центру трещины, ось х – параллельно поверхности, ось y – вдоль центрального сечения трещины (рис. 21). Очевидно, что составляющая Н_у поля Н_д над деталью равна нулю. Рассмотрим изменение поля по осям х и z по отдельно взятой кривой напряженности H_д в точках 1 – 5. Разложим вектор H_д в этих точках на составляющие вдоль линии намагничивающего поля (тангенциальная составляющая Н_t) и перпендикулярную к нему (нормальная составляющая Н_п).

Неоднородность поля вызывает искажение поля как в тангенциальном, так и в нормальном направлениях. Действительно, в точке 1 H_x1 = 0; H_z1= H_д1max; в точке 2 H_z2 уменьшилась, H_x2 увеличилась; в точке 3 H_z3 = 0; H_x3 = H_д3 = +max; в точке 4 H_x4 уменьшилась, а H_z4 поменяла знак; в точке 5 H_x5 = 0; H_z = H_д5 = – max. Аналогичные операции можно выполнить по каждой кривой напряженности H_д из всей совокупности поля рассеяния над дефектом, а затем, сложив тангенциальные и нормальные составляющие в каждой из пяти рассматриваемых по координатам х точках, построить графики изменения H_x(x_i) и H_z(x_i). Качественный вид зависимостей H_x(x) (без постоянной составляющей) и H_z(x) показан на рис. 21.

Рис. 21. Иллюстрация неоднородности магнитного поля над дефектом

Видно, что тангенциальная состав-ляющая напряженности поля H_х имеет максимум в центральном сечении дефекта, а нормальная составляющая H_z, проходя через нуль в этом сечении, имеет максимальные положительные и отрицательные значения в точках, рас-стояние между которыми несколько превышает ширину (раскрытие) трещины. Таким образом, изменения двух параметров – Н_х и Н_z – в пределах нескольких миллиметров (обычно 10 – 12 мм) в направлении намагничивания в зоне дефекта дают полную характеристику неоднородности магнитного поля дефекта.

Значения нормальной и тангенциальной составляющих соизмеримы в точках экстремумов. Сканирование деталей при поиске с регистрацией дефектов при их обнаружении приводит к формированию импульсов, форма и длительность которых будет зависеть примерно в равной степени для Н_п и Н_t от конфигурации, размеров и глубины залегания трещины, а также от напряженности приложенного магнитного поля и магнитной проницаемости ОК. Тем не менее в практике контроля предпочитают иметь дело только с функцией Н_z(х), которая за пределами дефекта «быстро» становится равной нулю. Это повышает достоверность контроля, к тому же постоянная составляющая функции Н_х(х) является помехой.

Известно, что в слабых магнитных полях, когда дифференциальная проницаемость металла велика (участок крутого подъема основной кривой намагничивания), значительная часть магнитного потока проходит в слое металла под трещиной, вследствие этого уменьшается индукция В₀ в зоне трещины, кроме того, само значение индукции мало. Все это приводит к незначительному уровню магнитного поля рассеяния над трещиной. В сильных магнитных полях (область насыщения, ) это приводит к ослаблению магнитной поляризации и, следовательно, к уменьшению H_д. Существуют оптимальные величины намагничивающего поля и магнитной проницаемости металла, когда магнитное поле Н_д при прочих равных условиях становится наибольшим. Такой режим соответствует магнитной индукции в металле порядка 0,8 – 0,9 Тл.

Видео:46. Граничные условия для электрического поляСкачать

Граничные условия для векторов напряженности и индукции магнитного поля

Вы будете перенаправлены на Автор24

При переходе границы между двумя магнетиками с разными магнитными проницаемостями $(mu )$ векторы напряжённости ($overrightarrow$) и индукции ($overrightarrow$) испытывают скачкообразные изменения, которые описываются граничными условиями.

Видео:Физика - Магнитное полеСкачать

Касательная составляющая вектора напряженности магнитного поля

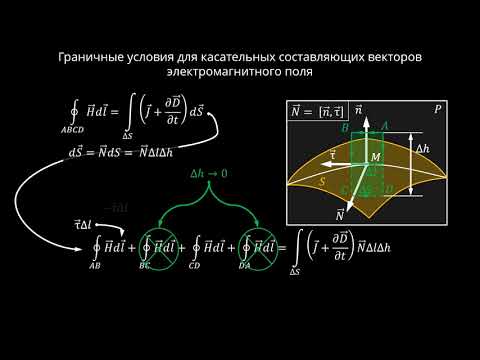
Получим граничное условие для тангенциальной составляющей вектора $overrightarrow$магнитного поля ($H_$). Предположим, что вдоль границы раздела течет поверхностный ток проводимости линейной плотности $overrightarrow$. Построим около границы магнетиков 1 и 2 замкнутый контур (рис. 1).

У этого контура высота пренебрежимо мала по сравнению с длинной основания $l$. Следовательно, вкладом в циркуляцию магнитного поля боковых сторон (AB и СD) пренебрежем. В таком случае имеем:

Правая часть выражения (1) имеет вид:

где $j_n$ —составляющая поверхностной плотности тока вдоль нормали к контуру $overrightarrow=left[overrightarrowoverrightarrowright] $(или, говорят в направлении перпендикулярном тому, в котором выбирают касательные составляющие $overrightarrow$). Надо отметить, что это поверхностные токи проводимости, а не молекулярные токи. Приравняем правые части выражений (2) и (3), получим:

В векторном виде имеем:

В том случае, если тока проводимости на границе раздела нет, то касательные составляющие $overrightarrow$на границе раздела непрерывны:

Видео:Лекция 6.5 | Нормальное и тангенциальное ускорение | Александр Чирцов | ЛекториумСкачать

Нормальная составляющая вектора магнитной индукции поля

Граничное условие для $B_n$получают из уравнения:

Перпендикулярные составляющие $overrightarrow$на границе раздела двух магнетиков непрерывны:

Готовые работы на аналогичную тему

Нормальная составляющая вектора $overrightarrow$Из уравнения (8), если применить материальное уравнение для векторов магнитного поля при переходе из одной среды в другую имеем:

Видео:2.5 Граничные условия для векторов поля на поверхности раздела средСкачать

Касательная составляющая вектора $overrightarrow$ магнитного поля

Тангенциальные составляющие магнитного поля испытываю скачек, причем:

Выражения (4, 6), (8), (9), (10) являются граничными условиями для магнитного поля. Они аналогичны граничным условиям для электрического поля.

Видео:Урок 222. Поток вектора напряженности электрического поляСкачать

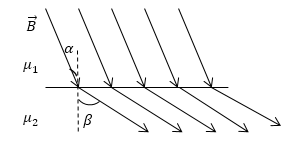
Закон преломления линий магнитного поля

Из граничных условий для магнитного поля следует закон преломления линий индукции:

где $_1$ — угол между линиями магнитной индукции в среде 1 и нормалью к поверхности раздела, $_2$- гол в среде 2. Так как в изотропных средах направления вектора $overrightarrow$ и вектора $overrightarrow$ совпадают, то закон (11) является и законом преломления линий напряженности. Из (11) следует, что если линии поля переходят из среды с меньшей магнитной проницаемостью в среду с большей проницаемостью, то они удаляются от нормали, и линии сгущаются.

Задание: На рис. 2 изображены линий вектора $overrightarrow $при переходе их одного магнетика ($_1$) в другой ($_2$). Какая из магнитных проницаемостей среды больше?

Рассмотрим, поведение силовых линий, когда они переходят границу двух магнетиков. Если отсутствуют поверхностные токи, выполняется условие:

Это означает, что в магнетике с большей магнитной проницаемостью, вектор $overrightarrow$ составляет больший угол с нормалью к границе раздела двух магнетиков.

Следовательно, в нашей задаче $_2 > _1$.

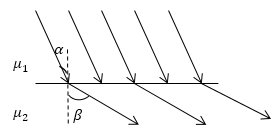
Задание: Магнитное поле на границе двух магнетиков изобразили с помощью линий поля (рис.3). Какие это линии, какая из магнитных проницаемостей среды больше?

1. На рис.3 изображены линии напряженности магнитного поля ($overrightarrow$), так как мы знаем, что они на границе магнетиков испытывают разрыв. Это является следствием связанных токов на границе раздела. Тогда как линии индукции магнитного поля не прерываются.
2. $_2 >_1,$ так как в среде с большей магнитной проницаемостью линии поля имею больший угол между нормалью к границе раздела сред согласно закону преломления.

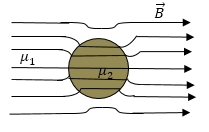
Задание: В однородное поле помещают шар из магнетика, изобразите линии индукции магнитного поля. Считайте, что магнитная проницаемость шара больше, чем проницаемость окружающей среды.

В ситуации, которая задана линии индукции в теле шаровой формы будут параллельными линиями, значение индукции во всех точках шара одинаковое. При этом будут постоянны напряженность и намагниченность, то есть, говорят, что шар намагничен однородно. Кроме того рис. 5 учитывает, что $_2 > _1.$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 11 02 2022

Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Граничные условия для векторов электрического и магнитного поля на границе раздела двух сред

А) Граничные условия для вектора электрической индукции.

Рассмотрим границу раздела двух сред с различными диэлектрическими проницаемостями и . Выделим на границе элементарный цилиндр, как показано на рис. 3.1.1.

Рис.1.4.1.Элементарный цилиндр, выделенный на границе раздела двух сред для определения граничных условий на вектор электрической индукции. и — нормали к поверхности S.

Согласно теореме Гаусса-Остроградского поток вектора электрической индукции через замкнутую поверхность S равен алгебраической сумме зарядов внутри объема V, ограниченного этой поверхностью:

(3.1.1)

Устремим высоту цилиндра к нулю . Тогда (3.1.1) преобразуется так:

(3.1.2)

Где , – компоненты вектора индукции, перпендикулярные границе раздела, S — площадь основания цилиндра.

Введем поверхностную плотность заряда:

(3.1.3)

Размерность поверхностной плотности заряда = Кл/м2 (Кулон на квадратный метр).

Тогда (3.1.2) можно переписать в виде

(3.1.4)

Если плотность поверхностного заряда равна нулю (), то

. (3.1.5)

Мы можем сформулировать следующее важное утверждение:

На границе раздела, не содержащей поверхностных зарядов, нормальная составляющая вектора электрической индукции непрерывна.

Б) Граничные условия для вектора магнитной индукции.

Рассмотрим границу раздела двух сред, обладающих различной магнитной проницаемостью. Из тех же соображений, что и в предыдущем пункте и принимая во внимание, что магнитных зарядов не существует, можно записать

(3.1.6)

Это равенство равносильно следующему утверждению:

На границе раздела двух сред нормальная составляющая вектора магнитной индукции всегда непрерывна.

В) Граничные условия для вектора напряженности электрического поля .

Рассмотрим снова границу раздела двух сред с различными диэлектрическими проницаемостями и . Выделим на границе замкнутый контур в соответствии с рис. 3.1.2. и используем закон электромагнитной индукции:

Где L — выбранный контур, L = 2 (1 + ) , S — площадь поверхности, ограниченная контуром L.

Рис.3.1.2. Контур на границе раздела двух сред, используемый при определении граничных условий для векторов напряженности электрического поля.

Устремим ширину контура к нулю, тогда поток вектора через поверхность S обратится в ноль, и мы получим

(3.1.7)

Откуда следует, что

(3.1.8)

Это равенство равносильно следующему утверждению:

На границе раздела двух сред касательная составляющая вектора напряженности электрического поля всегда непрерывна.

Г) Граничные условия для вектора напряженности магнитного поля Н.

Как в предыдущем случае выделим на границе раздела двух сред замкнутый контур L (рис.1.4.2). Воспользуемся законом полного тока

(3.1.9)

Где — плотность тока, протекающего через поверхность S, ограниченную контуром L.

Учтем, что вдоль границы раздела может течь ток проводимости, тогда при стремлении следует ввести поверхностную плотность тока:

(3.1.10)

Размерность поверхностной плотности тока [] = А/м. Теперь (3.1.9) можно переписать так:

Откуда следует, что

(3.1.11)

Это равенство равносильно следующему утверждению:

На границе раздела двух сред разность касательных составляющих напряженности магнитного поля равна поверхностной плотности тока.

При отсутствии поверхностного тока

(3.1.12)

Это равенство равносильно следующему утверждению:

На границе раздела двух сред, по которой не течет поверхностный ток, касательная составляющая магнитного поля непрерывна.

Д) Граничные условия на поверхности идеального проводника.

Определим идеальный проводник, как проводник, внутрь которого не может проникать электромагнитное поле . Для полей СВЧ-диапазона хорошие проводники (серебро, медь) можно в первом приближении рассматривать как идеальные. На поверхности такого проводника, тем не менее, может течь ток проводимости и формироваться поверхностный заряд. Поэтому на поверхности идеального проводника

, ,

, .

Силовые линии электрического поля перпендикулярны к поверхности идеального проводника; силовые линии магнитного поля касательны к поверхности идеального проводника, как показано на рис.3.1.3.

Рис.3.1.3. Силовые линии электрического и магнитного полей вблизи поверхности идеального проводника.

📽️ Видео

Билеты №18 и 19 "Теорема о циркуляции магнитного поля. Граничные условия"Скачать

Лекция 4-2. Условия на границе раздела двух диэлектриковСкачать

Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

Техника высоких напряжений ДолгиновСкачать

1.1 Векторы напряженности и индукции электрического и магнитного полейСкачать

ФИЗИКА. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ. ИС-19-3Скачать

Урок 225. Задачи на поток вектора напряженности электрического поляСкачать

Вектор Умова-Пойнтинга ● 1Скачать

Поляков П. А. - Электромагнетизм - Магнетики. Молекулярные токи. НамагниченностьСкачать

НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ суперпозиция полейСкачать

ЧК_МИФ (ЛИКБЕЗ) 3_2_1 ПРОХОЖДЕНИЕ СВЕТА ЧЕРЕЗ ГРАНИЦУ РАЗДЕЛА ДВУХ СРЕД -1 (Минимум теории)Скачать

Запись лекции на тему "Магнитные поля. Основные понятия"Скачать

Урок 218. Напряженность электрического поляСкачать