Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
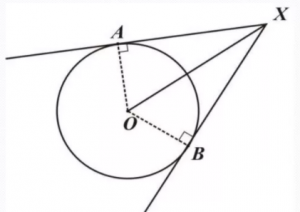
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
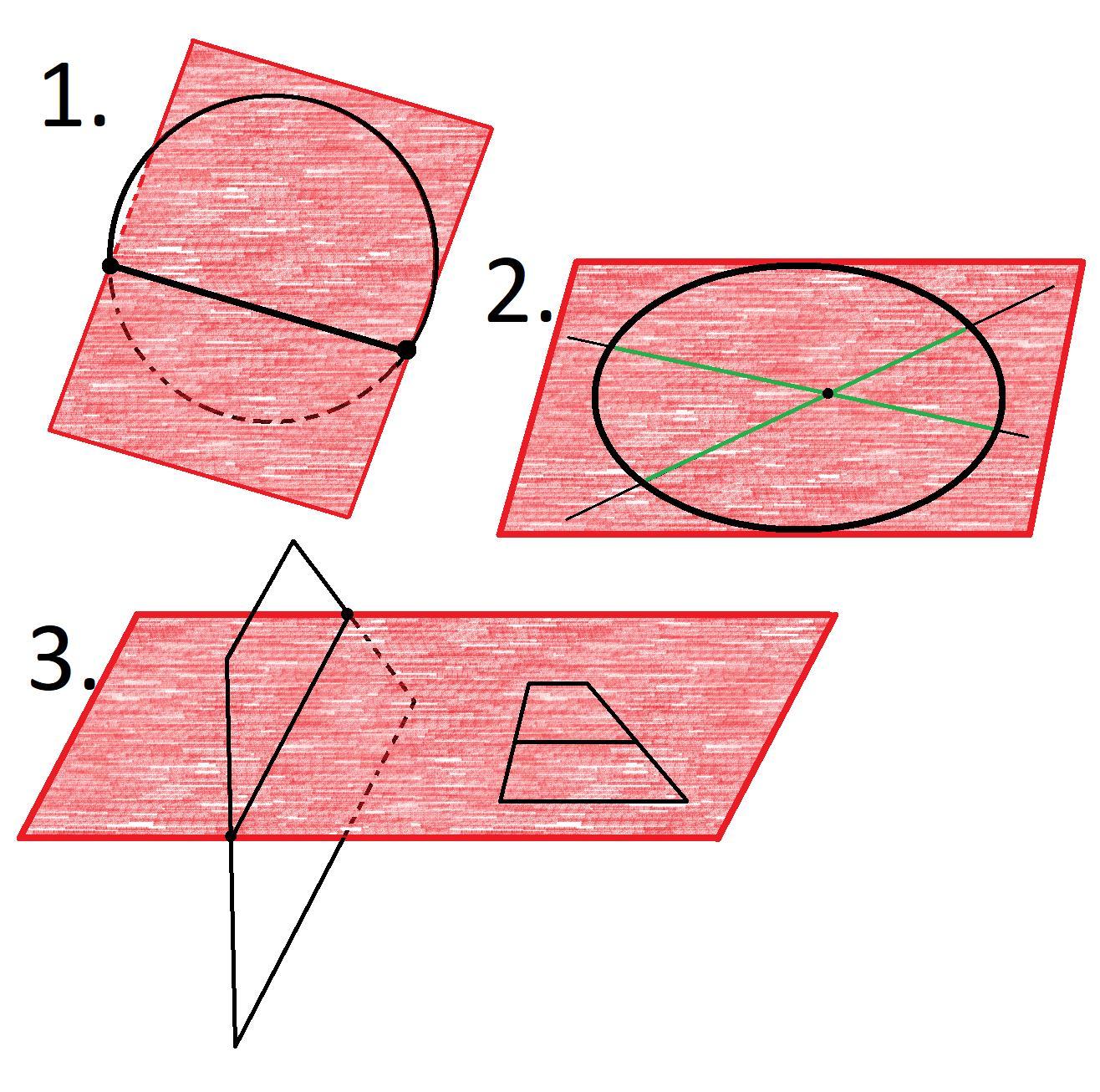
- 1Хорда окружности принадлежит плоскости, верно ли утверждение, что и вся окружность лежит в этой плоскости?
- 1а Через любые четыре точки, не лежащие на одной прямой, проходит плоскость и притом только однаДаНет2а Если три точки, принадлежащие прямой, лежат в плоскости, то все точки прямой лежат в этой плоско?
- Окружность имеет с плоскостью две общие точки?
- Прямая а лежит в плоскости альфа?
- Средняя линия трапеции лежит в плоскости а(альфа)?
- Какое из следующих утверждений верно?
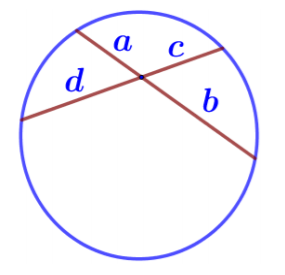
- Две пересекающиеся хорды окружности принадлежат плоскости?
- Верно ли утверждение : Если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости?
- Даны пересекающиеся плоскости альфа и бета?
- Аксиомы стереометрии?
- Верно ли утверждение : Прямая перпендикулярная плоскости, перпендикулярна любой прямой леж?
- Окружность и круг
- теория по математике 📈 планиметрия
- Определения
- Свойство хорд
- Длина окружности
- Дуга, касательная, круг, сектор, сегмент
- Свойства касательной
- 🌟 Видео
Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

1Хорда окружности принадлежит плоскости, верно ли утверждение, что и вся окружность лежит в этой плоскости?
Геометрия | 10 — 11 классы
1Хорда окружности принадлежит плоскости, верно ли утверждение, что и вся окружность лежит в этой плоскости?
2. 2 пересекающиеся хорды окружности принадлежать одной плоскости.
Верно ли утверждение, что любая точка окружности принадлежит этой плоскости?
3. средняя линия трапеции лежит в плоскости альфа.
Пересекает ли основание трапеции эту плоскость?
Окружность не всегда, но может пересекать эту плоскость.
Окружность лежит в данной плоскости т.
К. две пересекающие прямые (содержащие хорды, которые пересекаются), принадлежащие плоскости окружности, содержатся в данной плоскости.
А значит любая точка окружности так же принадлежит данной плоскости.
3. Нет, не пересекает.
Средняя линия параллельна основаниям.
Поэтому основания либо параллельно данной плоскости (по признаку параллельности прямой и плоскости), либо лежит в этой плоскости (ведь для параллельных прямых существует плоскость, в которой они лежат).
Среди возможны взаимных расположений прямой и плоскости нету такого, что прямая будет пересекать плоскость.
Видео:№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать

1а Через любые четыре точки, не лежащие на одной прямой, проходит плоскость и притом только однаДаНет2а Если три точки, принадлежащие прямой, лежат в плоскости, то все точки прямой лежат в этой плоско?
1а Через любые четыре точки, не лежащие на одной прямой, проходит плоскость и притом только однаДаНет2а Если три точки, принадлежащие прямой, лежат в плоскости, то все точки прямой лежат в этой плоскостиДаНет3а Через прямую и две точки, одна из которых лежит на прямой, а другая не лежит, проходит плоскость и притом только однаНетДа6в Если прямые EF и KL не лежат в одной плоскости, то прямые EK и LE не лежат в одной плоскостиДаНет7в Если две из четырех точек лежат на одной прямой, а две другие на прямой, пересекающей первую прямую, то все четыре точки лежат в одной плоскостиДаНет8в Если две хорды окружности лежат в плоскости, то и вся окружность лежит в этой плоскостиДаНет9в Через любые три точки круга, проходит плоскость и притом только однаДаНет10с Любая прямая, проходящая через точку пересечения медиан треугольника, имеет хотя бы одну общую точку с его сторонойДаНет11с Если два катета прямоугольного треугольника лежат в одной плоскости, то и весь треугольник лежит в этой плоскостиДаНет12с Если средняя линия трапеции лежит в плоскости, то и вся трапеция лежит в этой плоскостиДаНет.
Видео:На окружности по разные стороны от диаметра AB ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Окружность имеет с плоскостью две общие точки?
Окружность имеет с плоскостью две общие точки.
Верно ли , что все точки окружности принадлежат этой плоскости?
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Прямая а лежит в плоскости альфа?
Прямая а лежит в плоскости альфа.
Плоскость бета пересекает плоскость альфа по прямой б.
Известно, что прямая а пересекает плоскость бета в точке Б.
Где лежит точка Б?
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Средняя линия трапеции лежит в плоскости а(альфа)?
Средняя линия трапеции лежит в плоскости а(альфа).
Пересекают ли прямые, содержащие её основания, плоскость а(альфа)?
Видео:№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать

Какое из следующих утверждений верно?
Какое из следующих утверждений верно?
А) Если две точки окружности лежат в плоскости, то вся окружность лежит в этой плоскости ; б) прямая, лежащая в плоскости треугольника, пересекает две его стороны ; в) любые две плоскости имеют только одну общую точку ; г) через две точки проходит плоскость и притом только одна ; д) прямая лежит в плоскости данного треугольника, если она пересекает две прямые, содержащие стороны треугольника.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Две пересекающиеся хорды окружности принадлежат плоскости?
Две пересекающиеся хорды окружности принадлежат плоскости.
Верно ли утверждение, что любая точка окружности принадлежит этой плоскости?
Видео:№144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВССкачать

Верно ли утверждение : Если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости?
Верно ли утверждение : Если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости.
Поясните, пожалуйста, по подробнее.
Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Даны пересекающиеся плоскости альфа и бета?
Даны пересекающиеся плоскости альфа и бета.
Прямая с лежит в плоскости бета и пересекает плоскость альфа в точке С.
Прямая d лежит в плоскости альфа и пересекает плоскость бета в точке D.
По какой прямой пересекаются плоскости альфа и бета?
Помогите пж — та с задачей.
Видео:№652. На полуокружности АВ взяты точки С и D так, что ∪AC=37°, ∪BD=23°. Найдите хорду CD,Скачать

Аксиомы стереометрии?
Параллельность прямой и плоскости.
1. Прямая пересекает 2 стороны треугольника.
Лежит ли она в плоскости этого треугольника?
2. Прямая пересекает вершину треугольника.
Лежит ли она в плоскости этого треугольника?
3. Три вершины параллелограмма лежат в плоскости.
Принадлежит ли четвертая вершина параллелограмма этой плоскости?
4. Хорда окружности принадлежит плоскости.
Верно ли утверждение, что и вся окружность лежит в этой плоскости?
5. Две пересекающиеся хорды окружности принадлежат плоскости.
Верно ли утверждение, что любая точка окружности принадлежит этой плоскости?
6. Сколько плоскостей можно провести через : три различные точки ; две различные точки ; через прямую и не лежащую на ней точку ; через две параллельные прямые?
7. Верно ли утверждение : любые три точки принадлежат плоскости ; через любые три точки проходит единственная плоскость?
8. Известно, что прямая параллельна плоскости.
Параллельна ли она любой прямой, лежащей в этой плоскости Может ли данная прямая пересечь какую — либо прямую, лежащую в плоскости?
9. Средняя линия трапеции лежит в плоскости α.
Пересекают ли основания трапеции эту плоскость?
10. Прямая а параллельна линии пересечения плоскостей α и β.
Каково взаимное расположение а и α ; a и β?
11. Прямая b непараллельна линии пересечения плоскостей α и β.
Какого взаимное расположение b и α ; b и β?
Видео:№662 (исправлено) Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если ∪AD=54°Скачать

Верно ли утверждение : Прямая перпендикулярная плоскости, перпендикулярна любой прямой леж?
Верно ли утверждение : Прямая перпендикулярная плоскости, перпендикулярна любой прямой леж.
На этой странице сайта размещен вопрос 1Хорда окружности принадлежит плоскости, верно ли утверждение, что и вся окружность лежит в этой плоскости? из категории Геометрия с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 10 — 11 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.
30 : 5 = 6 см отрезок МЕ. Так значит ДМ = 24 см.
Скрещивающиеся прямые не имеют общих точек. У прямых AD и AB — общая точка A. У прямых AD и BD — общая точка D. У прямых AD и CD — общая точка D. ПрямыеAD и BC — скрещивающиеся.
BD — медиана и высота значит треугольник ABC равнобедренный, AB = BC, AD = DC, AB + AD = PABD — BD = 15 — 4 = 11 см PABC = 2 * (AB + AD) = 11 * 2 = 22 см периметр треугольника ABC = 22 cм.
ВС = АВ + АС Х = 6 + 9 = 15 ВС = 15.
Т. к точка А делит отрезок ВС на два отрезка, то этот отрезок ВС равен сумме двух получившихся отрезков, т. Е ВС = АВ + АС = 6 + 9 = 15. Ответ : отрезок ВС равен 15 сантиметрах.
Если О — центр окружности, то радиус окружности = 5. И АD = 5.
Подлежащие — одна черта, Сказуемое — две черты обстоятельство — точка пунктир Дополнение — пунктир.
Подлежащее одной чертой, сказуемое двумя, обстоятельство : _. _. _. В общем обстоятельство точка — тире, а дополнение пунктирной линией : — — — -.
Решение задачи во вложенном файле.
В прямоугольном ∆ АВС∠С = 90°, высота СК делит гипотенузу на отрезки АВ = 5 см, кВ = 1 см. Определите длину высоты СК. Высотапрямоугольноготреугольника, проведеннаяк гипотенузе, естьсреднеегеометрическое (среднеепропорциональное) между отрезками, н..
Видео:Окружность и круг, 6 классСкачать

Окружность и круг
теория по математике 📈 планиметрия
Определения
Окружность – множество всех точек плоскости, равноудаленных от одной данной точки (центра окружности). Другими словами – это замкнутая линия, длину которой можно измерить.
На рисунке центр окружности обозначен точкой О. 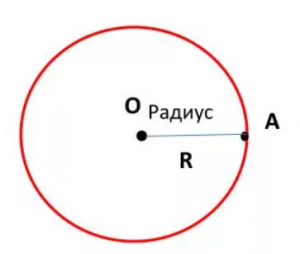
Радиус – расстояние от центра до любой точки окружности. На рисунке радиус обозначен АО. Все радиусы одной окружности равны. Радиус можно обозначать латинскими буквами R или r.
Диаметр – отрезок, который соединяет две точки окружности и проходит через её центр. На рисунке диаметр обозначен АВ. Все диаметры одной окружности равны. В одном диаметре содержится два радиуса. Диаметр обозначается буквой d.
Хорда — длинный эластичный продольный тяж у хордовых животных; осевой скелет их предковых и некоторых современных форм. Тянется вдоль тела ниже центральной нервной системы и выше полости тела.
Свойство хорд
Хорда — длинный эластичный продольный тяж у хордовых животных; осевой скелет их предковых и некоторых современных форм. Тянется вдоль тела ниже центральной нервной системы и выше полости тела.
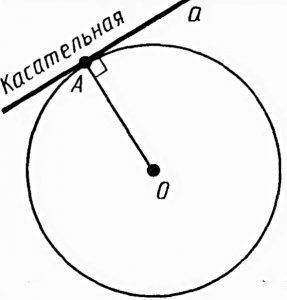
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Так, на рисунке показаны две пересекающиеся хорды, одна состоит из отрезков a и b, вторая из отрезков d и с, следовательно, ab=dс.
Длина окружности
Длину окружности можно вычислить по формуле:
C=2πR, где π=3,14.
Дуга – часть окружности, которая соединяет две точки. На рисунке мы видим несколько дуг, например, дуги CD (малая и большая). Дуга АВ – называется полуокружностью, так как стягивает концы диаметра. Обозначается дуга значком ∪АВ.
Видео:Окружность. 7 класс.Скачать

Дуга, касательная, круг, сектор, сегмент
Из точки, не лежащей на окружности можно провести касательную – прямую, которая имеет с окружностью только одну общую точку (рисунок 4).
Свойства касательной
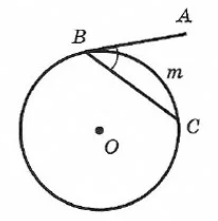
На рисунке видно, что АХ=ВХ, угол АХО равен углу ВХО.
Угол АВС (образован касательной АВ и хордой ВС) равен половине дуги m.
Круг – часть плоскости, ограниченная окружностью. Другими словами, круг – это всё, что находится внутри окружности.
Площадь круга вычисляется по формуле:
S=πR 2 , где π=3,14.
Сектор и его площадь
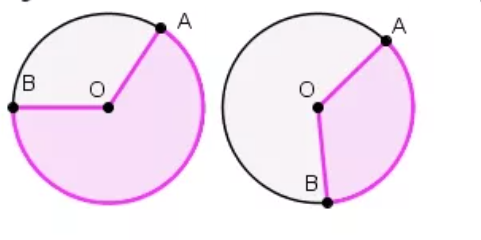
Сектор – область круга, ограниченная двумя радиусами. На рисунке сектор выделен сиреневым цветом, он ограничен радиусами ОА и ОВ.
Площадь кругового сектора вычисляется по формуле:
S= π R 2 360 . . × α , где α – угол между радиусами.
Сегмент – это область круга, ограниченная хордой и дугой. На рисунке сегмент выделен сиреневым цветом. Также можно сказать, что это часть круга, отсекаемая от него хордой. На рисунке видно, как
Хорда — длинный эластичный продольный тяж у хордовых животных; осевой скелет их предковых и некоторых современных форм. Тянется вдоль тела ниже центральной нервной системы и выше полости тела.
🌟 Видео
Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать

2020 точка О центр окружности на которой лежат точки A B и C известно что Угол ABC равен 62 градусаСкачать

№147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВССкачать
Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Демо ОГЭ по математике. Задание 17. Хорда окружности.Скачать

Уравнение окружности (1)Скачать