Точки по кругу в векторе

Сегодняшний урок мы посвятим тому как легко можно распределить векторные объекты на окружности.

Шаг 1.

Для примера мы будем использовать встроенные символы в иллюстраторе.

Шаг 2.

Разместив объект на рабочей поверхности дублируем его. Удерживая Alt перетягиваем его в сторону.

Выделяем оба объекта и нажимаем Alt+Ctrl+B, тем самым создаем переход между объектами.

Для того что бы задать желаемое количество переходов открываем панель «Параметры перехода».

Шаг 3.

Рисуем окружность на которой хотим разместить наши объекты. Для этого используем инструмент «Эллипс».

Шаг 4.

Выделяем наши объекты и окружность. Переходим Объект — Переход — Заменить траекторию.

Наши объекты размещаются по кругу окружности.

Шаг 5.

Что бы равномерно распределить объекты по окружности выбираем инструмент «Ножницы». После этого нажимаем в верхней точке нашей окружности.

Шаг 6.

Для того что бы можно было редактировать или заменить объекты на окружности ее надо разобрать.

Шаг 7.

Что бы заменить объект на окружности выбираем инструмент прямое выделение, нажимаем на объект, после в панели символов выбираем на что мы будем менять. В меню панели символов выбираем пункт «Заменить символ».

Важно что бы символы или объекты которые вы будете использовать были одного размера.

Видео:Как быстро расположить объекты по кругу в Adobe IllustratorСкачать

Основы Figma VII. Кривые

В седьмой части по основам Figma вы освоите работу с кривыми на продвинутом уровне. И хотя вы уже знакомы с булевыми операциями, которые позволяют создавать сложные векторные фигуры — это лишь верхушка айсберга. С помощью инструмента Pen (переводится как ручка или перо) можно воспроизвести буквально любую форму.

Зачем дизайнеру уметь работать с кривыми? Особенно пригодится в разработке собственных иконок, которые являются неотъемлемой частью любого интерфейса. Необязательно создавать пиктограммы с нуля, достаточно скачать подходящую заготовку и подправить/подогнать ее вручную под вашу задачу.

Во-вторых: отрисовка иллюстраций, к которым применимы те же приемы, единственное отличие: они обычно более сложны и выполняют другую функцию по сравнению с иконками (привлечение внимания).

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Кривые Безье

Кривые Безье — это математический аппарат для описания кривых, который использовал Пьер Безье в 1960-х годах для проектирования дизайна кузовов автомобилей компании Renault.

Впоследствии это открытие сыграло ключевую роль в проектировании и компьютерной графике в 2d и 3d направлениях. Фигуры на основе кривых Безье называют по-разному, в зависимости от приложения, но суть не меняется. Вы можете встретить такие термины: сплайны (spline) и «пути» (path).

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Виды кривых

Все кривые Безье можно условно поделить на несколько видов в зависимости от количества точек, из которых они составлены, что и определяет их сложность (смотрите рисунок сверху слева направо):

• линейные
• квадратичные
• кубические
• высших порядков

Обычно в графических приложениях используются последовательности кубических кривых Безье для построения любых форм. С теорией разобрались, переходим к практической части.

Видео:КАК РАСПОЛОЖИТЬ ОБЪЕКТЫ ПО ОКРУЖНОСТИ В ADOBE ILLUSTRATOR. 4 ПРОСТЫХ СПОСОБА!Скачать

Инструмент Pen в Figma

Для построения кривых в Figma используется специальный инструмент Pen (горячая клавиша P). Интересно, что с его помощью можно создать любой стандартный примитив (прямоугольник, круг и так далее). Более того, любой примитив можно быстро конвертировать в кривые. Но начнем мы с линейных кривых, особенность которых заключается в том, что контрольные точки не сглаживаются и итоговая фигура выглядит угловато.

Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Создание кривой

Последовательность действий для создания кривой выглядит так:

1. Выбираем Pen с помощью клавиши P или кликнув по иконке ручки на панели инструментов.
2. Кликаем в том месте, где хотим поставить первую точку. Обратите внимание, что верхняя панель мгновенно поменялась и теперь включает лишь 4 инструмента и кнопку «Done». Так Figma сигнализирует, что находится в режиме редактирования кривой.
3. Продолжаем кликать по рабочей области для задания новых точек. Как только у нас есть две точки, начинают появляться линии между ними.
4. Зажимаем клавишу Shift, чтобы временно ограничить угол наклона создаваемых линий и сделать их кратными 45 градусам. На практике это позволяет с легкостью рисовать идеальные горизонтальные, вертикальные и диагональные линии.
5. Чтобы указать последнюю точку фигуры есть несколько способов:
   • Нажать мышкой кнопку «Done» верхней панели.
   • Нажать Enter на клавиатуре.
   • Нажать Esc дважды. Первое нажатие заставит завершить создание кривой внутри векторного объекта. То есть вы можете продолжить кликать и создать еще одну линию в рамках одного слоя. Второе нажатие Esc заставит Figma выйти из режима редактирования.

Как видите, наша кривая получилась угловатой. Чтобы сгладить линию, вместо клика в процессе создания нужно зажать левую кнопку мыши и перемещать ее пока не получите нужную форму. Далее отпускаем левую кнопку мыши.

С помощью такого приема можно рисовать сглаженные линии. Поначалу это покажется сложным занятием, но с практикой вы поймете, что это достаточно удобно. Плюс вы всегда можете отредактировать векторную фигуру, о чем будет рассказано ниже.

Кроме того, можно создавать замкнутые фигуры, когда первая и последняя точки совпадают. Это позволит в дальнейшем закрасить замкнутые области.

Видео:Как быстро распределить объекты по окружности в Adobe IllustratorСкачать

Рисуем круг

Как я ранее упоминала, с помощью кривых можно нарисовать все что угодно. Знаю, что круг не самая сложная форма из возможных, но хорошее упражнение для новичка. К тому же, нам нужно попрактиковаться в построении сглаженных и замкнутых фигур. Чтобы упростить себе задачу, я нарисовала вспомогательную сетку. Дело в том, что при рисовании идеального круга, нужно отметить точки на одинаковом расстоянии и с идентичными степенями сглаживания. Приступим.

Помните, что создавать точки нужно зажимая левую кнопку и двигая курсор. Отпускать левую кнопку следует только в тот момент, когда вы будете удовлетворены кривизной линии. Выделите хотя бы 10 минут времени и попрактикуйтесь в рисовании сглаженных контуров, что бы приноровиться.

Видео:Физика - движение по окружностиСкачать

Редактирование кривых

Как и в случае с примитивами, вы можете изменить пропорции векторных объектов просто выделив их и потянув за любой из углов или сторон. Но на этом возможности редактирования не заканчиваются, вы можете:

• Добавить еще линий
• Изменить или переместить точки
• Настроить кривизну
• Добавить заливку замкнутым контурам

Для начала нужно войти в режим редактирования:

Выделить векторный объект. Это может быть не только кривая, но и большинство примитивов: прямоугольник, эллипс, линия и так далее.

Далее один из вариантов ниже:

• Нажать клавишу Enter
• Сделать двойной клик по векторному объекту. В этом случае предварительно выделять не нужно. Пожалуй это самый простой способ.
• Кликнуть по левой иконке квадратика (Edit Object) сверху в центре.

После этого панель инструментов преобразится. Слева появятся новые кнопки для работы с инструментами редактирования сплайнов.

Видео:Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Инструмент Move. Перемещение точек

Горячая клавиша V. Позволяет выделить и переместить одну или несколько точек векторного объекта мышкой. Тут работает зажатие клавиши Shift, как и при построении новой кривой. Также для перемещения точек можно использовать клавиатуру (клавиши с стрелками). Этот инструмент активируется по-умолчанию, когда вы переходите в режим редактирования.

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Инструмент Bend. Управление кривизной

Сначала активируем инструмент Bend (в переводе означает сгибать, что уже подсказывает назначение), кликнув по иконке закругленной линии с двумя точками (вторая справа) на панели инструментов. Для управления сглаживанием линии:

1. Подносим курсор к любой линии между двумя точками. В правом нижнем углу курсора появится иконка изогнутой линии.
2. Зажимаем левую кнопку мыши и тянем. Линия начнет повторять ваши движения, пытаясь подстроится под положение курсора. Если фигура была угловатой, то одновременно появятся направляющие точек, которые и задают кривизну.
3. Отпускаем левую кнопку мыши, чтобы зафиксировать кривизну.

Для управления сглаживанием через точку кривой:

1. Подносим курсор к любой точке кривой. В правом нижнем углу курсора появится иконка с точкой и двумя направляющими.
2. Зажимаем левую кнопку мыши и тянем. Из точки вытянется две симметричные направляющие, линии по бокам точки сгладятся. Чтобы управлять лишь одной направляющей, зажмите кнопку Alt. Чтобы включить привязку к углу наклона (кратная 45 градусам), зажмите кнопку Shift.
3. Отпускаем левую кнопку мыши, чтобы зафиксировать кривизну.

Ниже показаны все вышеперечисленные приемы, включая использование клавиш Shift и Alt:

Для управления сглаживанием через направляющие точки:

1. Подносим курсор к любой направляющей точки кривой. В правом нижнем углу курсора появится иконка с точкой и двумя направляющими.
2. При клике левой кнопкой мыши направляющая будет удалена.
3. Кликаем левой кнопкой мыши и тянем курсор, чтобы изменить угол направляющей вместе с противоположной направляющей, то есть симметрично. Если вы хотите изменить угол исключительно одной направляющей, зажмите клавишу Alt. Также тут работает зажатие клавиши Shift для привязки к углу наклона.

Часто случается, что направляющих не видно, но по форме линии видно, что они там есть. В таких случаях нужно переключиться на инструмент Move и выделить нужную точку. Появятся направляющие, после чего нужно переключиться назад в режим Bend.

Не самый удобный способ показать направляющие. Но есть решение. Достаточно постоянно работать в режиме Move, чтобы выбирать точки и показывать направляющие. А в режим Bend переходить с помощью горячей клавиши Ctrl или Command на MacOs. Обратите внимание, что горячую клавишу нужно зажать пока вы используете инструмент, так как сразу после отпускания клавиши вы вернетесь в режим Move.

Посмотрим, как это выглядят на практике. Обратите внимание, мы начинаем в режиме Bend, видны направляющие только двух точек. Далее переключаемся в режим Move, выделяем нужные точки и зажимаем Ctrl (Command на MacOs), чтобы быстро подправить направляющие точек или кривизну линий:

Видео:Как разместить объекты по кругу в Adobe Illustrator | Инструмент "Поворот" #OrlovillustratorСкачать

Инструмент Paint Bucket. Заливка замкнутых контуров

Позволяет выборочно закрасить замкнутые контуры векторной фигуры. Настройки заливки доступны в секции Fill и полностью повторяют возможности обычных примитивов. Инструкция по использованию:

1. Выбираем инструмент кликнув по иконке капли или нажав горячую клавишу B.
2. Кликаем внутри замкнутого контура, чтобы закрасить область. К иконке капли добавится плюсик.
3. Повторно кликаем внутри закрашенного контура, чтобы убрать заливку.

Видео:Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Настройка обводки

Мы уже знакомы с некоторыми настройками обводки из первого урока по Figma. Давайте теперь разберем и продвинутые опции:

• Выпадающие меню внизу слева и справа задают форму начальной и конечной точки контура. Конечно, если контур замкнутый, то мы ничего не заметим.
• По клику на иконку с тремя точками внизу справа можно получить доступ к продвинутым настройкам. Смотрите пункты ниже.
• Stroke style — стиль обводки: Solid — сплошная, Dashed — пунктирная. При выборе пунктирного стиля добавляются дополнительные параметры: Dash — длина пунктира, Gap — длина пропуска, Dash cap — форма пунктира.
• Join — форма соединения точек: Miter — автоматически скашивается если угол наклона меньше заданного полем Miter angle, Bevel — постоянно скошенная, Round — скругленная.

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Скругление углов

Скруглить точки кривой можно, и альтернативным способом:

1. Выделите сплайн и перейдите в режим редактирования.
2. Выделите нужные точки.
3. Укажите степень скругления в поле Corner radius в панели свойств справа.

Заметьте, что такой способ скругления не влияет на направляющие точек и работает только с угловатыми контурами. Если вы задали кривизну линий с помощью инструмента Bend, то скругление не будет работать.

Видео:Попадание точки в заданную область. Круг в круге. Уроки программирования на С++.Скачать

Добавление и удаление точек

Как я упоминала выше, добавить и удалить точки можно в любой момент. Предварительно войдя в режим редактирования, попробуйте следующее для копирования точки:

1. Выбираем инструмент Move (клавиша V).
2. Наводим курсор на точку, которую хотим скопировать.
3. Зажимаем кнопку Alt. Курсор изменится на двойной, как бы подсказывая нам, что готов к копированию точки.
4. Зажимаем левую кнопку мыши и перетаскиваем курсор. Новая точка последует за курсором. Обратите внимание, что образуется еще одна линия, так как оригинальная точка была связана линией с другой.

Для добавления точки внутри существующей линии:

1. Выбираем инструмент Pen (клавиша P).
2. Наводим курсор внутрь линии туда, куда собираемся добавить точку. Figma будет подсказывать нам середину линии. Также к курсору в правом нижнем углу добавится плюсик.
3. Делаем клик левой кнопкой мыши. Точка добавлена.

Для удаления точки:

1. Выбираем инструмент Pen (клавиша P).
2. Наводим курсор на точку, которую хотим удалить.
3. Зажимаем клавишу Alt. К курсору добавится минус в правом нижнем углу.
4. Делаем клик левой кнопкой мыши. Точка удалена.
5. Еще один хороший вариант: если выделить точку инструментом Move и удалить ее кнопкой Delete, то Figma не будет соединять соседние точки и может образоваться отдельный контур внутри слоя. Этот способ идеален если вы удаляете отдельные контуры, например, лишние элементы скачанной иконки, чтобы упростить ее.

Добавлять точки можно и вне существующих линий. В таком случае векторный объект будет состоять из нескольких контуров.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Преобразование обводки в кривые

На некоторых этапах работы, а особенно перед экспортом иконки в формат SVG может понадобиться преобразовать все линии в контуры. Другими словами конвертировать обводку в закрытые контуры с заливкой. Это нужно делать для того, чтобы иконки корректно отображались в браузере. После этой операции вы уже не сможете настроить толщину обводки или любые другие ее свойства кроме цвета. Поэтому выполняйте эту операцию в последнюю очередь. Чтобы конвертировать есть несколько способов:

• Выделите векторный объект и нажмите Ctrl + Shift + O или Shift + Command + O на MacOs.
• Вызовите контекстное меню нажав правой кнопкой мыши на нужном векторном объекте. Выберите команду Outline stroke.

Чтобы убедиться, что преобразование прошло успешно достаточно войти в режим редактирования и увидеть новые точки и кривые.

Видео:Центростремительное ускорение. 9 класс.Скачать

Сайты с бесплатными иконками

Теперь вы знаете большинство приемов работы с кривыми. Во втором уроке по работе с Figma вы узнали, как импортировать файл с помощью перетаскивания. Тогда мы использовали растровые файлы, но с векторными SVG-файлами все происходит точно также.

Существует множество сайтов с бесплатными SVG-иконками. Они удобны тем, что позволяют искать по ключевым словам. Тут нам не обойтись без знаний английского языка или Google Translate. А вот и наш список:

• The Noun Project — 3 000 000+ (да, более 3-х миллионов) бесплатных иконок с удобным поиском. Много готовых наборов по темам.
• Font Awesome — 1600+ бесплатных иконок в одном стиле с рубрикатором.
• Cursor.in — крошечный сайт с коллекцией всех курсоров MacOs.

Чтобы скачать иконку на The Noun Project, воспользуйтесь строкой поиска. Для примера я ввела ключевое слово energy и нажала Enter. Загрузится список иконок, по понравившейся нужно кликнуть. В открывшейся странице нужно нажать кнопку Get this icon. Далее выбираем Basic Download, потом Continue. Теперь нажимаем кнопку SVG. Иконка скачивается.

Видео:Построение окружности по трём точкам.Скачать

Экспорт в SVG

Для экспорта иконки в SVG-файл ее нужно предварительно подготовить:

1. Создать пустой фрейм и вставить внутрь векторный объект. Их может быть несколько. Размеры фреймов для иконок обычно кратны 8 пикселям. Подойдут такие: 16×16, 24×24, 32×32 и так далее. Если иконка не влазит, уменьшаем ее.
2. Выровнять иконку по центру фрейма. Убедиться, что вертикальные и горизонтальные отступы равномерные.
3. Перевести все обводки в кривые.
4. Перекрасить все элементы в черный цвет. Дело в том, что разработчики умеют перекрашивать иконки, если нужно.

Теперь все готово. Осталось выполнить сам экспорт:

1. Выделяем фрейм с иконкой.
2. В правой панели кликаем по плюсику напротив секции Export (она последняя).
3. В выпадающем меню меняем формат на SVG.

Видео:КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Домашнее задание

1. Выберите 8 иконок и нарисуйте их с использованием инструмента Pen.
2. Задание повышенной сложности. Выполнять необязательно. Выберите 4 иконки, упростите их и сделайте обводку потолще.
3. Подготовьте все нарисованные иконки и экспортируйте их в две отдельные папки (light, regular — для толстых). Убедитесь, что иконки имеют понятные названия. Поместите две папки в zip-архив. Самостоятельно научитесь архивировать файлы, если не умеете.

Видео:Ускорение при равномерном движении по окружностиСкачать

Выводы

В этом уроке вы познакомились с продвинутыми техниками работы с кривыми. Объединив эти знания с булевыми операциями можно рисовать иконки и иллюстрации любой сложности. Но это уже больше специализация графического дизайнера. Вам же важно научиться, как можно подправить существующую иконку и подогнать ее под ваши задачи.

Придумывание и отрисовка иконок это очень широкая и сложная тема, которую мы еще не раз затронем в дальнейшем.

Видео:Как расставить объекты по кругу | Adobe Illustrator | Расположение объектов по окружностиСкачать

Знакомимся с вектором

Основы линейной алгебры для тех, кого это миновало в универе.

Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное.

Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно.

⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях.

Видео:Как быстро распределить объекты по окружности в Corel DrawСкачать

Линейная алгебра

Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.

Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.

Например, мы знаем, что если a + b = c , то a = c − b . Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой.

Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.

В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.

Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.

Что такое вектор

Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.

Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве

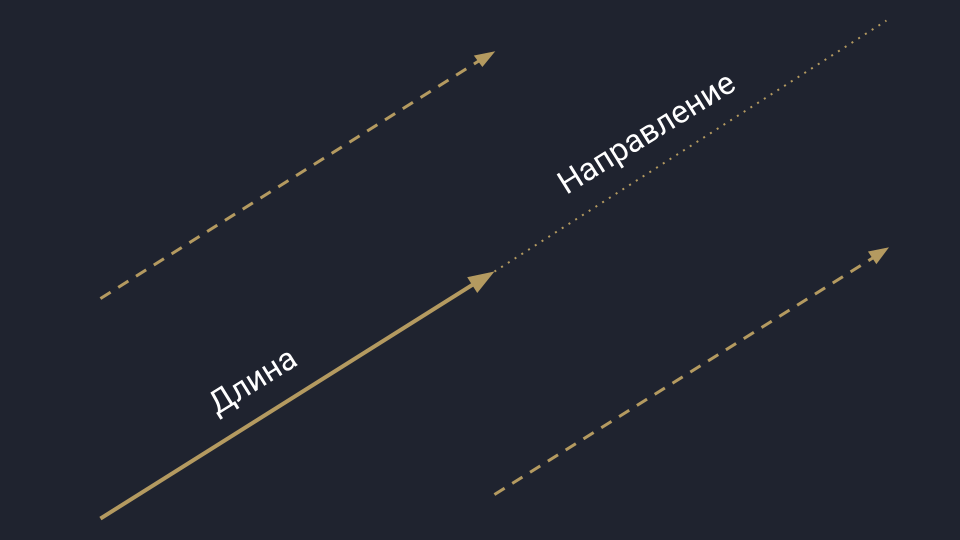
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.

Аналитическое представление вектора: данные можно перевести в числа

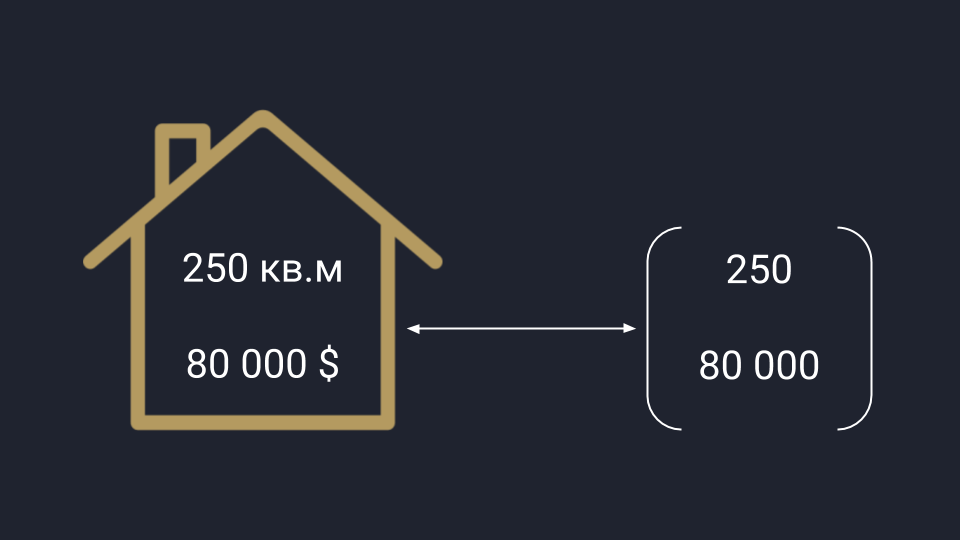
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.

Математическое представление вектора: данные можно перевести в числа или график

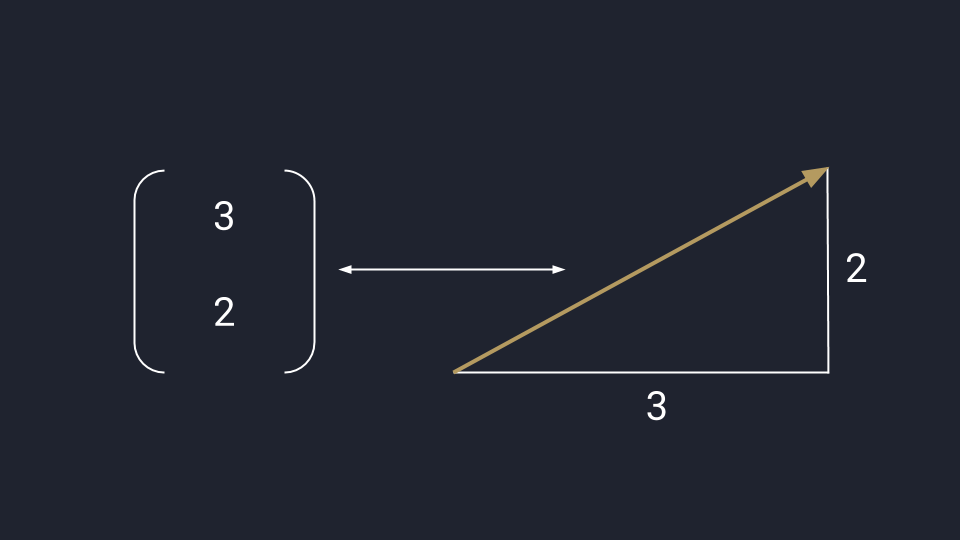
В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.

Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат

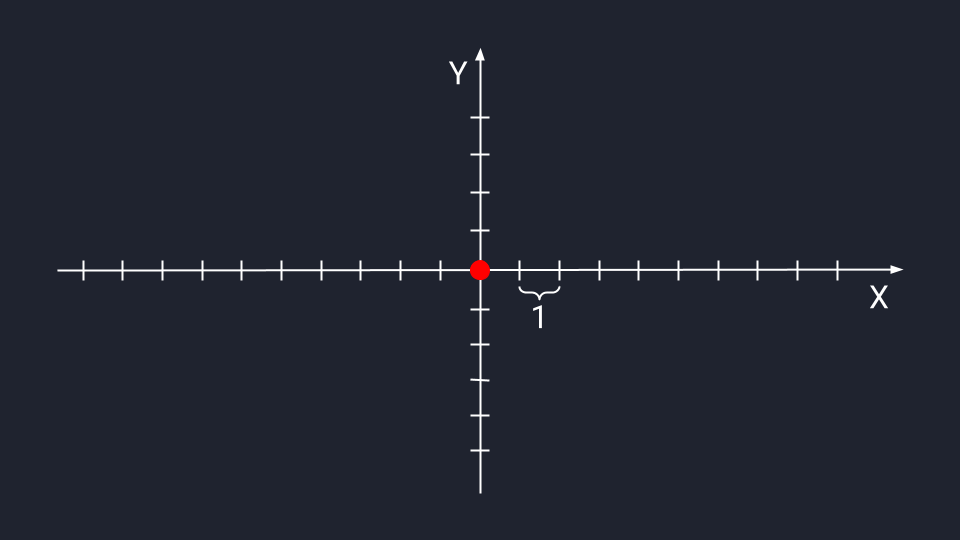
👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.

Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.

Как записывать

Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.

Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.

Способы записи вектора

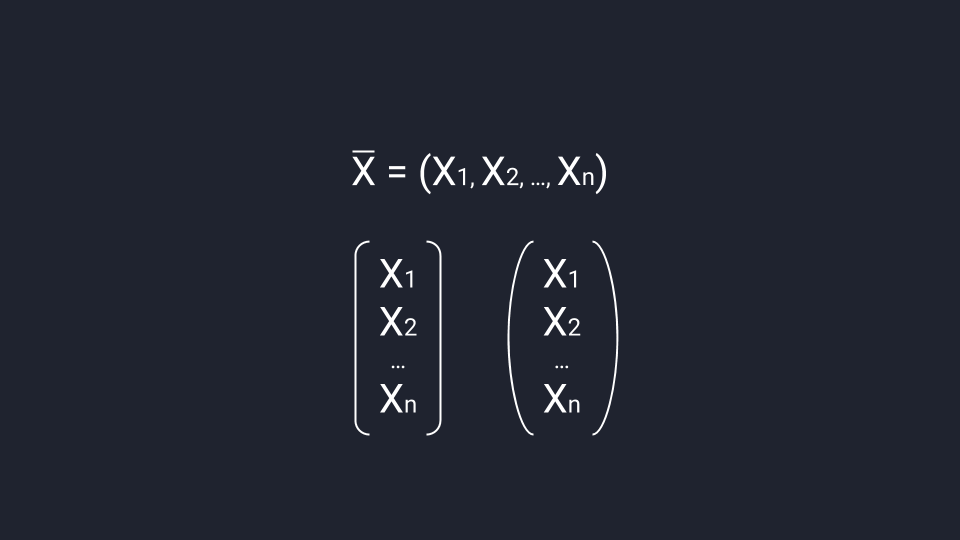
Скаляр

Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.

Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.

Как изображать

Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.

Графическое представление скаляра. Записывается в круглых скобках

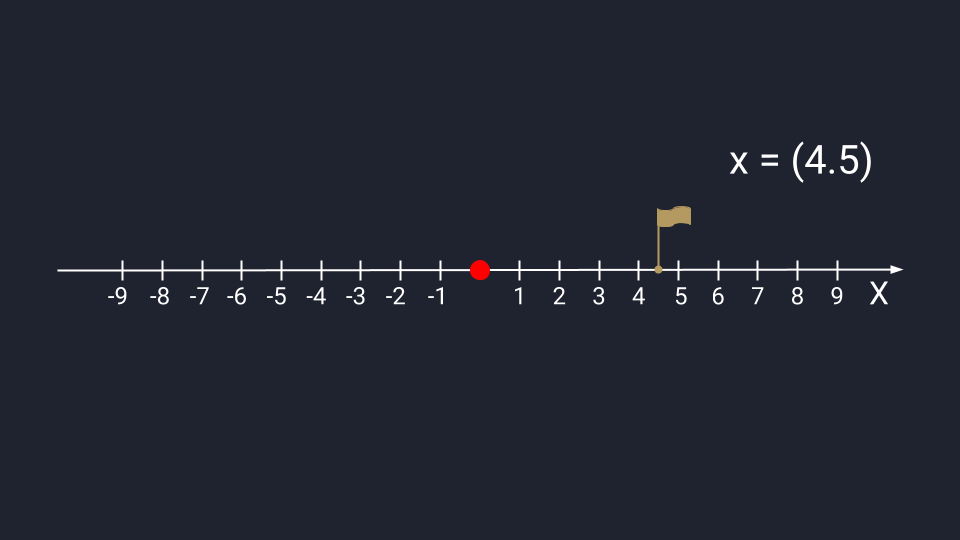
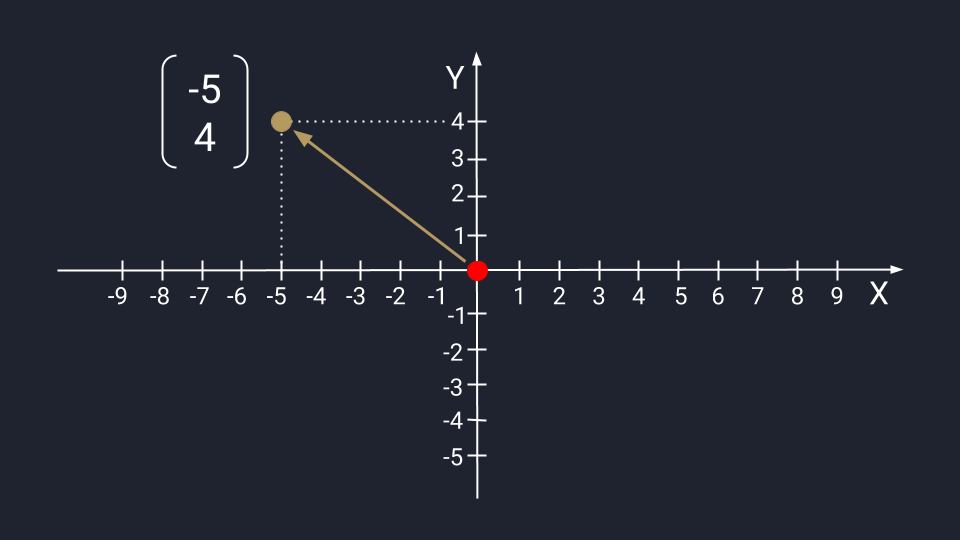
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.

Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.

Графическое представление числового вектора в двух измерениях

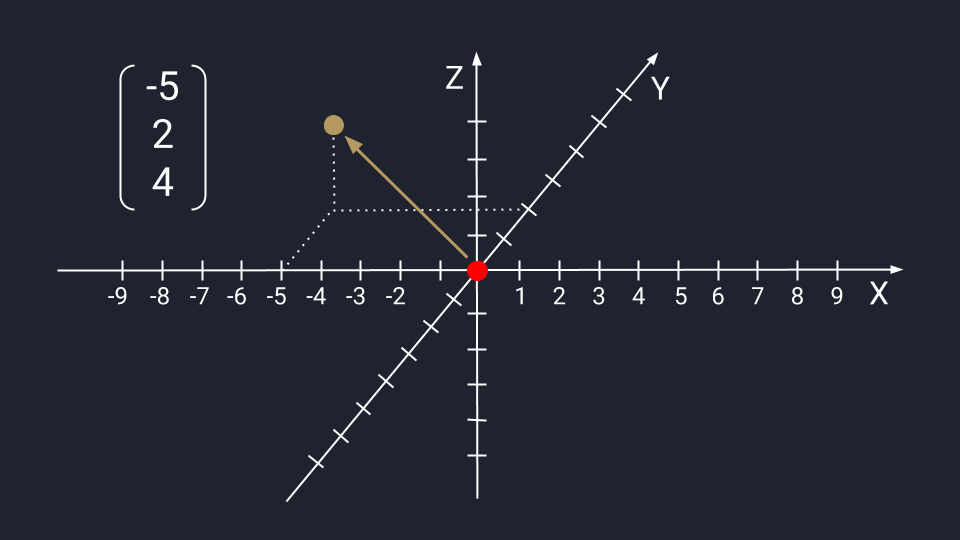
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.

Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.

Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4

Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.

Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.

И зачем нам это всё

Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:

• На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
• Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.

Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.

И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.

Что дальше

В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.