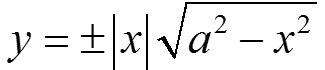Окружность разделена параболой на две части найти площади обеих частей (3 видео)

§ 50. Геометрическое приложение определённого интеграла

Рассмотрим несколько примеров.

Пример 1. Вычислить площадь параболического сегмента, отсечённого от параболы у2 = ах (о > 0) прямой х — Ь (см. рис. %>-

-Параболический сегмент ограничен сверху графиком кривой У2 = — ¦/ах, снизу графином кривой у = —fax и справа прямой х — Ь. Имеем:

Пример 2. Найти площадь, ограниченную параболой у — х2 и прямой х 4- у — 2 — 0 (см. рис. 97).

Решение. Найдём абсциссы xi и х^ точек пересечения Ли В пря-мой аг-Ьу — 2 = 0и параболы у ¦ решая совместно эти уравнения. Имеем: х^ + х — 2 = 0, т.е. х: — -2, хч — I. Тогда

Пример 3. Вычислить площадь, ограниченную параболами у = = 4 — х2, у = X2 — 2х (см. рис, 98),

Решение. Найдем абсциссы Яі и точек А и В пересечения параОол: 4-х7 — х2 — 2х х2 — х — 2 = Os = 2, Тогда

2 ^ ,2 = J (4-2®a + 2ar) неза штрихованной — причём S2 — 7tR2 — Si = Sir — Si. Найдём Si. На отрез ках OD и DC соответствующие криволинейные трапеции ограничены сверху и снизу кривыми, имеющими разные уравнения.

S = SOADBO + SQACBD

= j [v^ — + j [ye xa — ^—/8-л2^] dx.

Абсциссу хп найдём совместным решением уравнений окружности и параболы: у — & — ху2 = 2х отсюда 2х = 8 — х2 ИЛИІ1 + 2Ї-8 = 0, X> = —4> Х2

Точка С есть пересечение окружности а:2 4- j/2 ¦=? 6 с осью Ох, поэтому — 8, хс (Зс > 0). Следовательно,

= 2 dx + 2 у/&-х2 + 2J.

Для вычисления / воспользуемся результатом примера Имеем

i ф-ііу)) и прямыми у = 0 при а где ,2 і a — « где с»5 = ¦ 72 .

Длина дуги синусоиды у — с cose, 0 ^ я ^ 2тг равна

= J yf+liF ^ = 4 j Vl + c2^2®

-4- с2 cos2 f fit —

= «j* VTT^- с2sin2tdt — (fc,ї), fc= ) = [ fT

k2 зіи21 dt нааыпается эллиптическим интегралом

и через элементарные функции не выражается; для ник составлены таблицы при различных значениях к и tp.

Пример 12. Найти длину линии у = 1па- от Xi = л/3 до x 3 (см. рис. П1);

a) S, — | j (6stat-3)(-2eint)A =

У („а + со» И +ЛК)Л = 6 + ^ — V^) =

Пределы интегрирования (ij и І2) найдены из уравнения Gsinfc 3

и равны ti ¦= гц-. ?з =

6) & = j [у — 4) dx = 4 I [4(1 — cost) — 4](1 — cost) dt —

Пределы интегрирования ti = t^ = ^ найдены из уравнения 4 =

— 4(1 — cosi)» COS4 = 0.

b)Sb = 2 f 2/2 sin11 12/2 cos2 isiai) dt

= -24 j Sin2 t sina 2t dt = -12 J (1 — co$2?) sin2 21 dt

= -6 (t — і sin — I siti3 2t

Пример 14, Найти длину дуги кривой. заданной параметрическн.

а) х я= 4fa>s? +t sin t)r у = Длина дуги в этом случае

определяется формулой (х[ > 0)

х = R він t, dx = Л cos ? dx, S = ii — I2 — Ц — l).

Пример 18. Найти объём тела, ограниченного поверхностями х2 4- + у2 ^ н s2 + у2 4- z2 ^ 2Дат.

Решение. Совместное решен не уравнения конуса а;2 + = 3-z2

и шара г2 4* ї/3 ™ (г — — R2 да?т г — 0, г — — R (см. рис, 117). Искомый объём равен V = V2 — V]., где

Kl = | 5К ds = j + dz — j 3itz2dz = 0 0 0

SK — площадь поперечного сечения конуса,

j j ir(x2+y2)dz = І x(2zR

— площадь поперечного сечении шара. Искомый объём равен 1/ — Я11.

Пример 19. Найти объём тела, ограниченного поверхностями х2 + у2 — 5 — г н х2 4- у2 = 4z <см, рис, 118), 2. 5 Н

/ ч 1 0 X у Рис I1S

Решение. Совместное решение уравнений двух параболоидов даёт 5 — z = 4z, z 1, Иском мй объём равен

4zdz + Jtt(5 — z)dz— Ютг,

Пример 20. Найти объём тела, ограниченного поверхностями х2 + у2 = и х2+у

=2г2 -1 (см, рис. П9). Z

Решение, Совместное решение уравнения конуса х^ у* = z1 и двухполостного гиперболоида х

— 2z2 — 1 даёт z = 1, = —1.

Искомый объём равен V — 2(УК — Vf), где объём конуса irR2h —

h = 1, Я = 1, a Vr — j тг(2z* — 1) dz = | (л/2 — 1) ,

тогда V Щ- (2 — у/2) .

Пример 21« Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями = + уг = — 1 и і = 0, а также площадь этой фигуры (см,рис.

К — 7Г | (у?» 1/1) da * | (Зс

S — | (fft — = Йх — -h

Пример 22, Фигура ограничена линиями у = /(a:)t у = 0, х — х = Ь, В какой точке Мі(?ьуі) графика фуЕікцнн у = f(x) нужно провести касательную к нему так, чтобы она отсекала от фигуры трапеиню наибольшей площади? (см. §36),

Решение, Уравнение касательной в точке Afi(asi,j/x) графика функции у = f(x) есть у — Дяі) — — ^i), а площадь трапеции

Из условия ^^ = 0 находим (xi — /»C^i) = далее см. § 36,

Ответ: її — jft =в /(®i).

Пример 23. Прн как ил значениях параметра А» площади ограни-ченная линиями,

]) у = х 4- 2х — 4 и у = kx 2) у

Решение. Площадь фигуры, ограниченной линиями у =; аз2 + 4- Ьх н- с и у = кх +¦ bi, определяется формулой

S | | (уг — yi) dx j = J J (foe + fci — ax2 —

(fc — 6)(»1 + sa) — | (a? + ЦХ2 +®a)] J ‘

Предполагается, постоянные a, c, f>i такие, что прямая и парабола пересекаются, тогда точки пересечения находятся из уравнения ах2 -Ь + bx -h с ^ кх + bi или ах2 + х(Ь — fc) + с — Ец = 0. Отсюда

При ?> > О парабола и прямая пересекаются, D =0 парабола касается прямой а при D i), решение которой определяется условиями задачи.

1) Пусть ух = х2 + 2а: — 4 н у2 = кх, Тогда S<k) —

2) Пусть = ж2 — 4 и у2 ^ кх + 3, тогда S(k) = і (Л2 + 28)3’*

54*) = о при Аг — 0, тогда S(0) = Щvf,

Пример 24- Через данную точку М0(:со51/о). лежащей внутри параболы у — ах2 4- 4- с, дровссти прямую, отсекающую от параболы сегмент наименьшей площади.

Решение. Зап ишем прямую в виде I/ — 2/о — — ^о) » тогда площадь сегмента есть

где xi и лг^ абсциссы точек пересечения прямой и параболы определи ЕОТСЯ из уравнения у0 4- к(х — = ах2 toe -i- с или ах1, 4- — Л)4 + ? — Уо 4* fc^O — О И равны

(Ь- к)2 — 4а(с -уо+ кх0).

Подставляя xi и х2 в формулу для площади сегмента, получим

Из условия S'(k) — 0 находим к = Ь 4- 2oxq.

(уо — axj — йхо — с)’? .

Заметим, что прямая с угловым коэффициентом к

Ь—2ахо, про ходящая через точку Mo(z0)i/0), параллельна касательной к параболе у — ах2 4- Ьх 4-с в точке А1г(х0; org 4- Ьх0 + с). Если точка А/п(яо,!Л>) лежит на параболе, то у0 = ах^ 4- 4- с н Snijn = 0.

Пример 25. Прямая, проходящая чере^ точку Аґ0(я0іуо) образует с положи тельными полуосями координат треугольник. Найти мини 390

Таким образом, площадь сегмента будет иметь наименьшее значе-ние при угловом коэффициенте к = Ь + 2аго, при этом

дельное значение площади треугольника н написать уравнение этой прямой (см. задачу 3 §4),

Решение. Площадь треугольника S = ^ аб, а уравнение прямой

& отрезках (-7 = 1 Тогда — -Е- ^ = 1, а =

Аз уравнения -г- = 0 нашшм b— 2уа Искомая площадь Smin —

а — уравнение прямой есть — + = 1.

Пример 26. Фигура ограничена линиями у’^ (зс+2)2, у = О, О- Под каким углом к оси Ох надо провести прямые через точку (0,4), чтобы они разбивали фигуру на три равновеликие части (см. рис, 121). Решение.

(я + З)2da; = і (л + 2)а|° — |.

Так как Soon = Scbd *= Sbad> tbOD-OC= OD(OB — ОС) = = I — OD-OB или ОС = ВО — ОС т І — OB. Отсюда ОС —

ОБ —- Тогда искомые углы равны а і « arctg ^^ — arctg 9, аг = f OD , &

Пример 27, Найти площадь фигуры, ограниченной кривыми;

О У = |2 — |a?|j, у = 0f х = я = 4;

2) у — -ь х — 2|, у = 0, я = -2h ж — 2. у j j j D< 0,4) УН А ВС О х Рнс. 121

Решение, I) График функция у = |2 — |z| f показан з §38, Величина искомой площади равна сумме трех треуголыгикоа

3 = ^ ¦ 2 ¦ 2 -Ь ^ ¦ 4 ¦ 2 Н- ^ ¦ 2 * 2 — &

2) График функции у = ^х’2 4 — 2f изображён в §ЗЙ. Искомая площадь с учётам того, что данная функция является чётной функцией, равна

S = 2 | (і3 + х — 2) dx 4 2 f + .г — 2) сіх = | 4 у — 6.

Пример 28, Найти площадь фигур, ограниченной графиком функции у = $ 4 5 н касательными, проведёнными к этому графику в точках с абсциссами я = 0, х = 2 (см. рис. 122).

Решение. Так как уравнения касательных к графику функции у = X2 + 5 есть: у

5; 4х — у 4- 1 = 0, то искомая площадь равна (см, рис.)

5 = ^ЛЛ- Злэсго — Sbcd = j (з2 + 5) das — AC — CF —

Пример 29, Составить уравнение прямой, проходящей через начало координат и делящей криволинейный треугольник с вершиной в начале коорлинат, ограниченный линиями у = 2х — х2, у = О, х — 1, на две равновеликие части (см. рис. 123). У1 и О z^iq іс «7 1 А г Рис. 123

Решение. Уравнение прямой, проходящей через начало координат, имеет вид у = кх.

Зове = ОС-СБ = і Сії ^ I fc, так как ОС = 1, tga= fc =

So ас =| (2а- — = 2 Socb или — — к, отсюда к — -.

Уравнен не искомой прямой есть у = » х.

Пример 30. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной графиками функция аг 4* (у — а)* == = 1 (а > 1),

Решение. Искомый объём определяется го формуле

Ух = т J (у? — УІ) dx, где == О. ± /l — X2 ,

так как у — = 4а/1 — х2 „ то

Vx = it J 4а V* — я2 = 8їга j Vl — x2 dx = — J = 2тг2а,

Пусть кривая задагіа в полярной системе координат г = /¦( ) (см. § 7). В этом случае площадь сектора, ограниченного кривой г и ра

диусами-векторами if — Of и у — Т&п г

ЕСЛИ кривая есть окружность г = R, 0 ^ tp ^ 2тг, то

Ь = | + dtp = = 2тгR. о

Пример 31. Найти в полярной системе координат площадь и длину лунки, ограниченной дугами окружностей х1 у2 — 2Rx и х2 + у2

Решение. Уравнения заданных окружностей в полярной системе координат есть: т — 2Ясо5 ) dp ^ *r/4

Видео:Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать

Площадь фигуры в декартовой системе координат. Примеры

Уравнение верхней и нижней границы:

Пример 2

В каком отношении парабола y 2 = 2 x делит площадь круга x 2 + y 2 = 8 ?

Точки пересечения: x 2 + 2 x – 8 = 0 → x ₁ = –4, x ₂ = 2 ( x > 0) .

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Упражнения

1. Нарисуйте кривую, задаваемую уравнением r = sin 4 φ .

2. Нарисуйте кривую, задаваемую уравнением r = cos φ .

3. Для параболы x 2 = 4 ay выберем в качестве полярной оси луч, идущий по оси Oy с началом в фокусе F (0, a ) параболы. Переходя от декартовых к полярным координатам, покажите, что парабола с выколотой вершиной задается уравнением

4. Докажите, что уравнение

задает эллипс, если 0 > 1.

5. Нарисуйте спираль Архимеда, заданную уравнением r = — φ . Чему равно расстояние между соседними витками этой спирали?

6. Человек идет с постоянной скоростью вдоль радиуса вращающейся карусели. Какой будет траектория его движения относительно земли?

7. Нарисуйте гиперболическую спираль , задаваемую уравнением r = .

8. Нарисуйте спираль Галилея , которая задается уравнением r = a 2 ( a > 0). Она вошла в историю математики в XVII веке в связи с задачей нахождения формы кривой, по которой двигается свободно падающая в области экватора точка, не обладающая начальной скоростью, сообщаемой ей вращением земного шара.

9. Нарисуйте кривую, задаваемую уравнением r = | |.

10. Нарисуйте кривую, задаваемую уравнением r = .

11. Нарисуйте кривую, задаваемую уравнением r = .

12. Найдите параметрические уравнения: а) спирали Архимеда; б) логарифмической спирали.

1. Березин В. Кардиоида //Квант. – 1977. № 12.

2. Березин В. Лемниската Бернулли //Квант. – 1977. № 1.

3. Берман Г.Н. Циклоида. – М.: Наука, 1975.

4. Бронштейн И. Эллипс. Гипербола. Парабола / Такая разная геометрия. Составитель А.А. Егоров. – М.: Бюро Квантум, 2001. — / Приложение к журналу «Квант» № 2/2001.

5. Васильев Н.Б., Гутенмахер В.Л. Прямые и кривые. – 3-е изд. – М.: МЦНМО, 2000.

6. Маркушевич А.И. Замечательные кривые. – М.- Л.: Гос. изд. течн. – теор. лит., 1951. — / Популярные лекции по математике, выпуск 4.

7. Савелов А.А. Плоские кривые. – М.: ФИЗМАТЛИТ, 1960.

8. Смирнова И.М., Смирнов В.А. Кривые. Курс по выбору. 9 класс. – М.: Мнемозина, 2007.

9. Смирнова И.М., Смирнов В.А. Геометрия. Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2011.

10. Смирнова И.М., Смирнов В.А. Компьютер помогает геометрии. – М.: Дрофа, 2003.