Видео:9 класс. Геометрия. ОГЭ. Окружность. Четырехугольники.Скачать

И. Проверка домашнего задания
1. Проверить решение задачи № 24 по записям (с пробелами), сделанными на доске до начала урока.
Решение задачи № 24 Пусть АВ
1) ВС = 40 см, BD =. ; пусть AD = х см, тогда АС=. С ΔАВ D : АВ2 = х2 -122 = х2 — 144. Из ΔАВС АВ2. Тогда х2 — 144 = (х + 26)2 — 402; 52х=. ; х =15. Следовательно, AD=. AC = 41 см.
2) BD=. BC=7 см; пусть А D =. тогда AC = 2х см.
С ΔАВ D AB2=. Из Δ АВС АВ2 = 4х2 — 49.
Тогда х2 — 1 = . ; 3х2 = . ; х2 = 16. Отсюда х = . ; следовательно, AD =. AC = 2·4 = 8 (см).
Ответ. 1) 15 см и 41 см; 2) 4 см и 8 см.
2. Математический диктант.
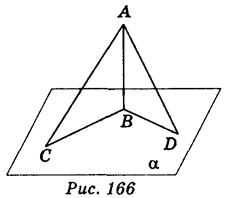
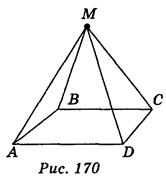
МО — перпендикуляр к плоскости ОАВ; 
Вариант 1 — МО = 1 см, ОА = 3 см, MB = 
вариант 2 — МЕ = 1 см, ОВ = 4 см, МА = 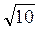
1) длину неизвестной наклонной; (2 балла)
2) длину неизвестной проекции наклонной; (2 балла)
3) длину отрезка АВ; (2 балла)
4) расстояние от точки В до середины отрезка АВ; (2 балла)
5) расстояние от точки М до середины отрезка АВ; (2 балла)
6) расстояние от точки А до плоскости ЯЗЫКОВ. (2 балла)
Ответ. Вариант 1.1) 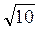

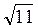
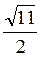
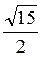
Вариант 2. 1) 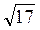
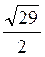
Видео:Геометрия Середина M стороны AD выпуклого четырёхугольника равноудалена от всех его вершинСкачать

II. Восприятие и осознание нового материала
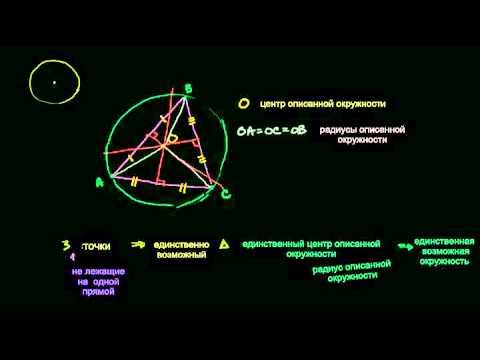
Свойство точки, равноудаленной от вершины многоугольника
Если через центр окружности, описанной вокруг многоугольника, проведено прямую, перпендикулярную к плоскости многоугольника, то каждая точка этой прямой равноудалена от вершин многоугольника.
Доведение
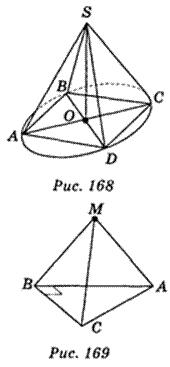
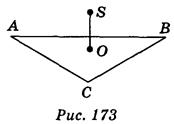
Пусть ABCD — четырехугольник, вокруг которого описана окружность с центром в точке О, и OS (ABC). Докажем, что SA = SB = SC = SD (рис. 168).
(ABC). Докажем, что SA = SB = SC = SD (рис. 168).
ΔASO = ΔBSO = ΔCSO = ΔDSO (за двумя катетами: SO — общая, АО = BO = CO = DO).
Из равенства треугольников следует, что SA = SB = SC = SD.
Если некоторая точка равноудалена от вершин многоугольника, то основание перпендикуляра, опущенного из данной точки на плоскость многоугольника, совпадает с центром окружности, описанной вокруг многоугольника.
Доведение
Пусть ABCD — данный четырехугольник, для точки S пространства SA = SB = SC = SD и SO
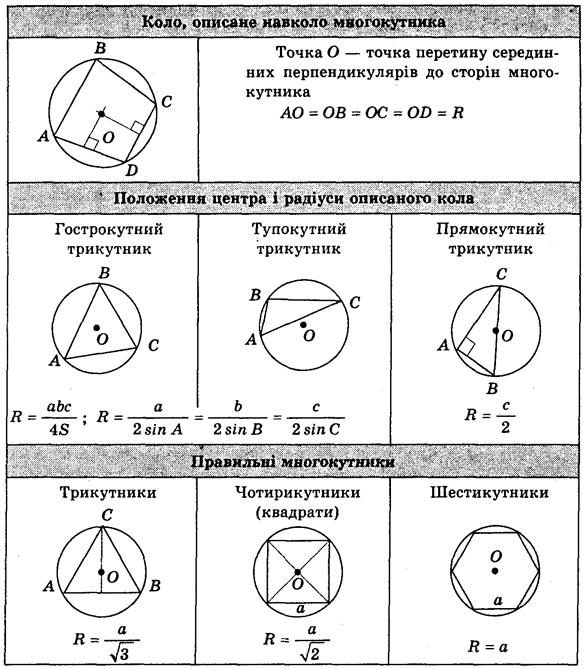
Далее следует напомнить формулы для нахождения радиуса круга, описанного вокруг некоторых многоугольников, с помощью данной настенной таблицы.
1. 
2. ABCD — квадрат, АВ = 4 
3. АВ = ВС = АС = 5 
4. ABCD — квадрат, SO

5. Δ АВС — правильный; точка О — центр треугольника; АВ = 3

6. Задача 21 из учебника (с. 35).
7. Задача 20* из учебника (с. 35).
III. Домашнее задание
Задачи № 6, 17-19 (с. 34-35).
IV. Подведение итога урока
Вопрос к классу
1) Какое свойство имеют точки, которые лежат на перпендикуляре, проведенном к плоскости многоугольника через центр окружности, описанной вокруг многоугольника?
2) Где находятся точки, равноудаленные от вершин некоторого многоугольника?
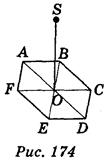
3) Через центр О правильного шестиугольника ABCDEF проведем перпендикуляр SO к плоскости АВС (рис. 174). Укажите, какие из приведенных утверждений правильные, а какие — неправильные:
а) расстояния от точки S до вершин шестиугольника ABCDEF разные;
б) угол OAS равен углу OCS;
в) если ОА = 1 cm, SO = 1 см, то SA = 
г) если SO = OB, то OSB = 60°.
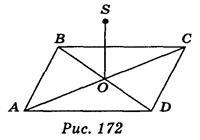
4) Расстояния от точки S до всех вершин прямоугольника ABCD равны, точка О — точка пересечения диагоналей АС и BD прямоугольника ABCD. Укажите, какие из приведенных утверждений правильные, а какие — неправильные:
а) прямая SO перпендикулярна к прямой АС;
б) прямая SO не перпендикулярна к прямой BD;
в) прямая SO перпендикулярна к плоскости АВС;
г) если АВ = 6 см, ВС = 8 см и AS = 13 см, то SO = 12 см.
Видео:Точка, равноудаленная от всех вершин многоугольникаСкачать

Точка равноудалена от всех вершин четырехугольника
Задание 26. Середина М стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если ВС = 6, а углы В и С четырёхугольника равны соответственно 124° и 116°.
В четырехугольнике ABCD точка M – середина AD и равноудалена от вершин A, B, C и D. Следовательно, AM=MD=MB=MC.
Пусть 

Учитывая, что сумма углов в любом треугольнике 180 градусов, имеем:
Рассмотрим треугольник BMC, в котором сумма углов равна
и треугольник BMC – равносторонний. Поэтому BM=BC=6 и AM=BM=6. Тогда сторона AD=2AM=2∙6=12.
Видео:Точка, равноудаленная от всех сторон многоугольникаСкачать

Середина $M$ стороны $AD$ выпуклого.
Задание:
Решение:
Так как точка $M$ равноудалена от всех вершин четырехугольника $ABCD$, то около этого четырехугольника можно описать окружность с центром в точке $M$.
=> Суммы противоположных углов четырехугольника $ABCD$ равны $180^$
Треугольник $AMB$ равнобедренный с основанием $AB$ ($AM=BM=R$)
=> угол $MAB$ равен углу $ABM=80^$
Треугольник $BMC$ так же равнобедренный ($BM=CM=R$) с основанием $BC$
🎬 Видео
Стереометрия 10 класс. Часть 1 | МатематикаСкачать

№952. Докажите, что середина гипотенузы прямоугольного треугольника равноудалена от всех его вершин.Скачать

№199. Точка S равноудалена от вершин прямоугольного треугольника и не лежит в плоскости этогоСкачать

Геометрия Четырехугольник оказался вписанным Задача №26 ОГЭСкачать

ОГЭ Задание 25 Свойство вписанного четырехугольникаСкачать

№951. Докажите, что четырехугольник ABCD является прямоугольником, и найдите егоСкачать

Четыре замечательные точки треугольникаСкачать

№143. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 смСкачать
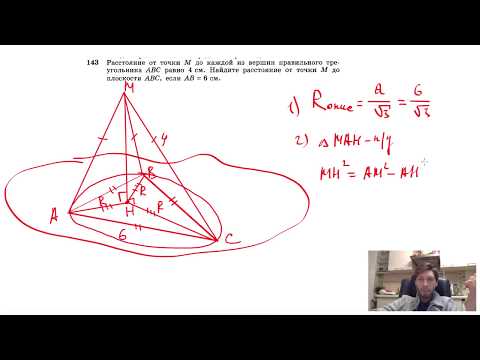
№202. Точка удалена от каждой из вершин прямоугольного треугольника на расстояние 10 см. На какомСкачать

Задача 3 ЕГЭ по математике. Урок 84Скачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

8 класс, 36 урок, Свойства серединного перпендикуляра к отрезкуСкачать

№949. На оси абсцисс найдите точку, равноудаленную от точек: а) А (1; 2)Скачать

Как найти площадь прямоугольника? Попробуй решить задачуСкачать

№369. Найдите углы A, B и C выпуклого четырехугольника ABCD, еслиСкачать

Три точки, задающие окружностьСкачать