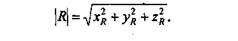Вектор нормали к эллипсоиду (4 видео) | Курс школьной геометрии

Вектор нормали к эллипсоиду

Таким образом, нормаль к эллипсу в данной точке делит отрезок, заключенный между центром и проекцией этой точки на большую ось эллипса, в постоянном отношении, равном c 2 : b 2 .

Пусть точке M отвечает (при растяжении эллипса) точка M’ описанной окружности и пусть нормаль NM в точке M пересекает продолжение радиуса OM’ в точке Q. Докажем, что OQ = a + b. Применим теорему Менелая к треугольнику OM’M₁ и секущей QN:

После упрощений получаем OQ = a + b.

Итак, если при сжатии точке M’ описанной около эллипса окружности соответствует точка M эллипса, то нормали в этих точках к соответствующим кривым пересекаются в точке, расположенной на окружности радиуса a + b с центром в центре эллипса.

Пусть теперь нормаль к эллипсу в точке M пересекает малую ось эллипса в точке S. Найдем предельное положение S₀ точки S, когда точка M приближается вдоль эллипса к вершине B малой оси. Продолжим нормаль до пересечения в точке Q с окружностью радиуса a + b с центром в точке O, и пусть прямая OQ пересекает описанную около эллипса окружность в точке M’. Тогда имеет место пропорция QM : MS = QM’: M’O = b : a. Когда точка M приближается к точке B, то QM → a и BS₀ = a 2 : b. Это и есть радиус соприкасающейся окружности к эллипсу в вершине малой оси. Аналогично находим, что b 2 : a есть радиус соприкасающейся окружности в вершине большой оси эллипса.

Содержание

Основные линии и плоскости эллипсоида
Контрольные вопросы и упражнения:
Вычисление нормалей и углов отражения
📽️ Видео

Видео:Вектор нормали к поверхности поля в точкеСкачать

Основные линии и плоскости эллипсоида

Прямая Мп (рисунок 3) перпендикулярная касательной плоскости N к эллипсоиду в точке ее касания М, называется нормалью.

Рисунок 3 — Нормаль к поверхности эллипсоида

Любая плоскость, проходящая через нормаль, называется нормальной плоскостью. Через нормаль можно привести бесчисленное множество нормальных плоскостей, из которых плоскость меридиана и плоскость первого вертикала являются основными.

Нормальная плоскость (рисунок 4), проходящая через нормаль точки М и малую ось эллипсоида, называется плоскостью геодезического меридиана данной точки. Сечение поверхности эллипсоида этой плоскостью дает след, называемый геодезическим меридианом. Нормальная плоскость Ы₂, перпендикулярная к плоскости геодезического меридиана, называется плоскостью первого вертикала. Сечение поверхности эллипсоида этой плоскостью дает след, называемый первым вертикалом.

Плоскость, перпендикулярная к малой оси эллипсоида и проходящая через его центр, называется плоскостью экватора. Сечение поверхности эллипсоида этой плоскостью дает след, называемый экватором.

Видео:Математика Без Ху!ни. Касательная плоскость и нормаль к поверхности.Скачать

Контрольные вопросы и упражнения:

1. Что называется геоидом?
2. Что такое земной эллипсоид и какими элементами он определяется?
3. Перечислить основные линии и плоскости эллипсоида?

Рисунок 4 — Плоскость меридиана и плоскость первого вертикала

Видео:Геометрия. 9 класс. Уравнение прямой. Направляющий вектор и вектор нормали прямой /22.10.2020/Скачать

Вычисление нормалей и углов отражения

Тема9. Построение реалистических изображений

В этом разделе мы рассмотрим методы, которые позволяют получить более-менее реалистичные изображения для объектов, моделируемых многогранниками и полигональными сетками.

Модели отражения света

Рассмотрим, как можно определить цвет пикселов изображения поверхности согласно интенсивности отраженного света при учете взаимного расположения поверхности, источника света и наблюдателя.

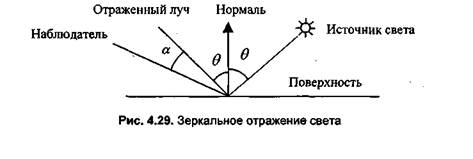
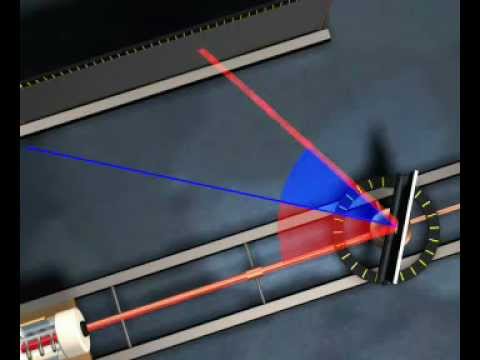
Зеркальное отражение света.Угол между нормалью и падающим лучом (Θ) равен углу между нормалью и отраженным лучом. Падающий луч, отраженный, и нормаль располагаются в одной плоскости (рис. 4.29).

Поверхность считается идеально зеркальной, если на ней отсутствуют какие либо неровности, шероховатости. Собственный цвет у такой поверхности не наблюдается. Световая энергия падающего луча отражается только по линии отраженного луча. Какое-либо рассеяние в стороны от этой линии отсутствует. В природе, вероятно, нет идеально гладких поверхностей, поэтому полагают, что если глубина шероховатостей существенно меньше длины волны излучения, то рассеивания не наблюдается. Для видимого спектра можно принять, что глубина шероховатостей поверхности зеркала должна быть существенно меньше 0.5 мкм

Если поверхность зеркала отполирована неидеально, то наблюдается зависимость интенсивности отраженного света от длины волны — чем больше длина волны, тем лучше отражение. Например, красные лучи отражаются сильнее, чем синие.

При наличии шероховатостей имеется зависимость интенсивности отраженного света от угла падения. Отражение света максимально для углов, близких к 90 градусам.

Падающий луч, попадая на слегка шероховатую поверхность реального зеркала, порождает не один отраженный луч, а несколько лучей, рассеиваемые по различным направлениям. Зона рассеивания зависит от качества полировки и может быть описана некоторым законом распределения. Как правило, форма зоны рассеивания симметрична относительно линии идеального зеркально отраженного луча. К числу простейших, но достаточно часто используемых, относится эмпирическая модель распределения Фонга, согласно которой интенсивность зеркально отраженного излучения пропорциональна (cosа) p , где а— угол отклонения от линии идеально отраженного луча. Показатель р находится в диапазоне от 1 до 200 и зависит от качества полировки. Запишем это таким образом:

где I— интенсивность излучения источника, K_s— коэффициент пропорциональности, который изменяется от 0 до 1.

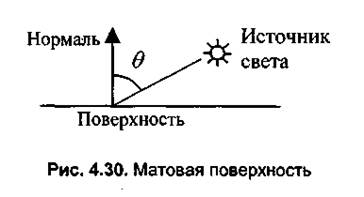
Диффузное отражение.Этот вид отражения присущ матовым поверхностям. Матовой можно считать такую поверхность, размер шероховатостей которой уже настолько велик, что падающий луч рассеивается равномерно во все стороны. Такой тип отражения характерен, например, для гипса, песка бумаги. Диффузное отражение описывается законом Ламберта, согласно которому интенсивность отраженного света пропорциональна косинусу угла между направлением на точечный источник света и нормалью к поверхности (рис. 4.30).

где I— интенсивность источника света, K_d— коэффициент, который учитывает свойства материала поверхности. Значение K_d находится в диапазоне от 0 до 1 . Интенсивность отраженного света не зависит от расположения наблюдателя.

Матовая поверхность имеет свой цвет. Наблюдаемый цвет матовой поверхности определяется комбинацией собственного цвета поверхности и цвета излучения источника света.

При создании реалистичных изображений следует учитывать то, что в природе, вероятно, не существует идеально зеркальных или полностью матовых поверхностей. При изображении объектов средствами компьютерной графики обычно моделируют сочетание зеркальности и диффузного рассеивания в пропорции, характерной для конкретного материала. В этом случае модель отражения записывают в виде суммы диффузной и зеркальной компонент:

где константы K_d, K_S определяют отражательные свойства материала.

Согласно этой формуле интенсивность отраженного света равна нулю для некоторых углов Θ и а. Однако в реальных сценах обычно нет полностью затемненных объектов, следует учитывать фоновую подсветку, освещение рассеянным светом, отраженным от других объектов. В таком случае интенсивность может быть эмпирически выражена следующей формулой:

где I_а — интенсивность рассеянного света, К_а — константа, изменяется от 0 до 1.

Можно еще усовершенствовать модель отражения, если учесть то, что энергия от точечного источника света уменьшается пропорционально квадрату расстояния. Использование такого правила вызывает сложности, поэтому на практике часто реализуют модель, выражаемую эмпирической формулой:

где R — расстояние от центра проекции до поверхности, k — константа.

Как определить цвет закрашивания точек объектов в соответствии с данной моделью? Наиболее просто выполняется расчет в градациях серого цвет (например, для белого источника света и серых объектов). В данном случае интенсивность отраженного света соответствует яркости. Сложнее обстоит дело с цветными источниками света, освещающими цветные поверхности. Например, для модели RGB составляются три формулы расчета интенсивности отраженного света для различных цветовых компонент. Коэффициент! К_а и K_d различны для разных компонент — они выражают собственный цвет поверхности. Поскольку цвет отраженного зеркального луча равен цвету источника, то коэффициент K_s будет одинаковым для всех компонент цветовой модели. Цвет источника света выражается значениями интенсивности I для соответствующих цветовых компонент.

Алгебра векторов

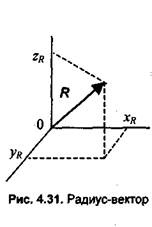
Здесь уместно сделать небольшое отступление от темы. Рассмотрим элементы алгебры векторов. Вектором называется отрезок прямой, соединяющий некоторые точки пространства А и В. Направление вектора — от начальной точки А к конечной точке В. Радиус-вектор R — это вектор, с начальной точкой в центре координат. Координатами радиус-вектора являются координаты конечной точки (рис. 4.31). Длина радиус-вектора часто называется модулем, обозначается как R|и вычисляется следующим образом:

Единичный вектор — это вектор, длина которого равна единице. Перечислим основные операции над векторами.

1. Умножение вектора на число X = Va. Результат — вектор X, длина которого в а раз больше вектора V. Если число а положительно, то направление вектора X совпадает с вектором V. При а