Теорема (о единственности разложения по данному базису) — раздел Математика, Линейная алгебра Разложение Любого Вектора .
Разложение любого вектора 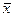
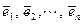
Доказательство.Предположим, что для вектора 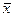
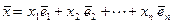
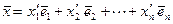
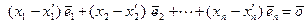
Поскольку базисные векторы линейно независимы, то из полученного равенства следуют равенства 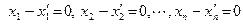
Следствие.Любые два вектора равны тогда и только тогда, когда равны их координаты в каком – либо базисе.
Таким образом, при фиксированном базисе линейного пространства каждый вектор однозначно определяется своими координатами в этом базисе.
Эта тема принадлежит разделу:
Линейная алгебра
На сайте allrefs.net читайте: «линейная алгебра»
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Теорема (о единственности разложения по данному базису)
Видео:Найдите разложение вектора по векторам (базису)Скачать

Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
Все темы данного раздела:
Линейное пространство
Множество элементов любой природы называется линейным или векторным пространством, а его элементы
Множество числовых функций
Рассмотрим множество числовых функций, определенных на некотором промежутке. Любым двум функциям и
Множество всех полиномов степени не выше
Элементами множества являются полиномы вида
Теорема (о существовании и единственности разности элементов)
Для любых двух векторов линейного пространства, существует такой единственный вектор
Теорема (об условиях равенства нулю произведения числа на вектор)
Произведение числа на вектор равно нулевому вектору тогда и только тогда, когда число равно нулю или вектор равен нулевому вектору. Доказательство.Пусть число
Определители матриц и их свойства
Определители вводятся только для квадратных матриц как некоторое правило, формирующее значение определителя по элементам матрицы. Если элементы матрицы числа, то определитель будет
Теорема (о разложении определителя по любой строке или столбцу)
Определитель порядка равен сумме произведений элементов любой его строки или столбца на соответствующие алгебраи
Доказательство
Напишем формулу разложения определителя по первой строке . Вид этой формулы не за
Теорема (об определителе произведения двух матриц)
Определитель произведения двух матриц равен произведению определителей матриц сомножителей . Теоре
Системы линейных уравнений
Общая система из линейных алгебраических уравнений с
Теорема (о существовании и единственности обратной матрицы)
Любая квадратная матрица имеет единственную обратную матрицу, вычисляемую по формуле , тогда и только тогда, ког
Доказательство
Докажем, что условие , является достаточным условием для существования обратной матрицы. На главно
Теорема Крамера
Если в квадратной системе уравнений определитель матрицы коэффициентов не равен нулю, то система имеет единственное решение, которое находится либо матричным способомпо формуле
Доказательство
В соответствии с теоремой о существовании и единственности обратной матрицы, для невырожденной матрицы коэффициентов нашей системы существует единственная обратная матрица
Теорема (о линейных свойствах координат векторов)
При сложении любых двух векторов их координаты в данном базисе складываются, а при умножении любого вектора на любое число координаты умножаются на это число. Доказательство
Доказательство
По определению базиса это означает, что любая строка или столбец матрицы могут быть представлены в виде линейной комбинации базисных строк или базисных столбцов, причем единственным образом. Все ра
Доказательство
Покажем достаточность условия второго следствия. Если строки матрицы линейно зависимы, то по свойству системы зависимых векторов одна из строк является линейной комбинацией остальн
Теорема (о приведении к ступенчатой матрице)
Любую матрицу можно привести к ступенчатой матрице, выполнив конечное число элементарных преобразований. Теорема доказывается конструктивно путем перебора конечного числа возможных
Теорема (о ранге ступенчатой матрицы)
Ранг ступенчатой матрицы равен числу ее ненулевых строк. Доказательство.Ненулевые, ступенчатые строки линейно независимы, что можно показать, составив линейную комб
Теорема (о равносильных переходах)
Любое конечное число элементарных преобразований системы переводят ее в систему, равносильную исходной системе. Доказательство теоремы следует непосредственно из оп
Доказательство
Ранг матрицы коэффициентов системы по определению всегда меньше или равен числа уравнений или числа неизвестных исх
Исследование и решение однородных систем уравнений
Однородная система всегда совместна, так как имеет нулевое (тривиальное) решение
Доказательство
Необходимость.Пусть есть конечномерное пространство размерности
Теорема (о виде общего решения неоднородной системы уравнений)
Решение неоднородной системы уравнений всегда может быть представлено как сумма общего решения соответствующей
Векторная алгебра
Под векторной алгеброй обычно понимают раздел линейной алгебры, изучающий геометрические векторы на плоскости и реальном пространстве. В математике и ее приложениях встречаются разл
Евклидовы пространства
Определение.Скалярным произведением двух любых векторов линейного пространства называется правило, по которому каждой упорядоченной паре векторов
Доказательство
Пусть есть ортогональная система ненулевых векторов евклидова пространства. Предположим, что выполняется ра
Теорема (основные свойства ортонормированного базиса)
1. Координаты произвольного вектора в ортонормированном базисе равны скалярным произведениям этого вектора на соответствующие векторы этого базиса. 2. Скалярное произведение двух
Определение
Каноническим базисом в пространстве трехмерных геометрических векторов называют векторы
Векторное и смешанное векторно-скалярное произведения
Определение.Векторным произведением двух геометрических векторов и
Теорема (о модуле векторного произведения )
Модуль векторного произведения двух векторов и
Линейные геометрические объекты
Определение.Пусть есть некоторый ненулевой вектор, а
Видео:10 класс, 45 урок, Разложение вектора по трем некомпланарным векторамСкачать

Векторное пространство: размерность и базис, разложение вектора по базису
В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.
Введем некоторые определения.
Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.
Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:
e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )
Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.
Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.
Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.
Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.
Переставив местами в исходной системе другие векторы, получим еще один базис.
Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.
Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.
Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.
Рассмотрим применение данной теории на конкретных примерах.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 )
Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.
Решение
Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.
A = 3 2 3 — 2 1 — 1 1 2 — 2 A = 3 — 2 1 2 1 2 3 — 1 — 2 = 3 · 1 · ( — 2 ) + ( — 2 ) · 2 · 3 + 1 · 2 · ( — 1 ) — 1 · 1 · 3 — ( — 2 ) · 2 · ( — 2 ) — 3 · 2 · ( — 1 ) = = — 25 ≠ 0 ⇒ R a n k ( A ) = 3
Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.
Ответ: указанные векторы являются базисом векторного пространства.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 ) d = ( 0 , 1 , 2 )
Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.
Решение
Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , — 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , — 1 , — 2 ) является базисом.
Ответ: указанная система векторов не является базисом.
Исходные данные: векторы
a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )
Могут ли они являться базисом четырехмерного пространства?
Решение
Cоставим матрицу, используя в качестве строк координаты заданных векторов
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
По методу Гаусса определим ранг матрицы:
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
1 2 3 3 0 1 0 2 0 1 — 1 1 0 1 — 2 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 — 2 — 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4
Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.
Ответ: заданные векторы являются базисом четырехмерного пространства.
Исходные данные: векторы
a ( 1 ) = ( 1 , 2 , — 1 , — 2 ) a ( 2 ) = ( 0 , 2 , 1 , — 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )
Составляют ли они базис пространства размерностью 4?
Решение
Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.
Ответ: нет, не составляют.
Видео:Разложение вектора по базису. 9 класс.Скачать

Разложение вектора по базису
Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.
Таким образом, мы пришли к формулировке важнейшей теоремы:
Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.
Докажем эту теорему:
зададим базис n -мерного векторного пространства — e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :
x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n — некоторые числа.
Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:
Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:
1 — x 1 ) · e ( 1 ) + ( x
2 — x 2 ) · e ( 2 ) + . . . ( x
Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x
2 — x 2 ) , . . . , ( x
n — x n ) будут равны нулю. Из чего справедливым будет: x 1 = x
n . И это доказывает единственный вариант разложения вектора по базису.
При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .
Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.
Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .
Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.
Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x
Вектор x → будет представлен следующим образом:
2 · e ( 2 ) + . . . + x
Запишем это выражение в координатной форме:
( x 1 , x 2 , . . . , x n ) = x
1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x
2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x
n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x
2 e 1 ( 2 ) + . . . + x
2 e 2 ( 2 ) + + . . . + x
n e 2 ( n ) , . . . , x
2 e n ( 2 ) + . . . + x
Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x
n e 2 n ⋮ x n = x
Матрица этой системы будет иметь следующий вид:
e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )
Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x
n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .
Применим рассмотренную теорию на конкретном примере.
Исходные данные: в базисе трехмерного пространства заданы векторы
e ( 1 ) = ( 1 , — 1 , 1 ) e ( 2 ) = ( 3 , 2 , — 5 ) e ( 3 ) = ( 2 , 1 , — 3 ) x = ( 6 , 2 , — 7 )
Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.
Решение
Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .
Используем метод Гаусса:
A = 1 — 1 1 3 2 — 5 2 1 — 3
1 — 1 1 0 5 — 8 0 3 — 5
1 — 1 1 0 5 — 8 0 0 — 1 5
R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.
Пусть в базисе вектор x → имеет координаты x
3 . Связь этих координат определяется уравнением:
3 e 1 ( 3 ) x 2 = x
3 e 2 ( 3 ) x 3 = x
Применим значения согласно условиям задачи:
Решим систему уравнений методом Крамера:
∆ = 1 3 2 — 1 2 1 1 — 5 — 3 = — 1 ∆ x
1 = 6 3 2 2 2 1 — 7 — 5 — 3 = — 1 , x
1 ∆ = — 1 — 1 = 1 ∆ x
2 = 1 6 2 — 1 2 1 1 — 7 — 3 = — 1 , x
2 ∆ = — 1 — 1 = 1 ∆ x
3 = 1 3 6 — 1 2 2 1 — 5 — 7 = — 1 , x
Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x
Ответ: x = ( 1 , 1 , 1 )
Видео:Геометрия 9 класс (Урок№7 - Разложение вектора по двум неколлинеарным векторам. Координаты вектора.)Скачать

Связь между базисами
Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:
c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
Указанные системы являются также базисами заданного пространства.
n ( 1 ) — координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:
1 ( 1 ) e 1 ( 1 ) + c
2 ( 1 ) e 1 ( 2 ) + . . . + c
n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c
1 ( 1 ) e 2 ( 1 ) + c
2 ( 1 ) e 2 ( 2 ) + . . . + c
n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c
1 ( 1 ) e n ( 1 ) + c
2 ( 1 ) e n ( 2 ) + . . . + c
В виде матрицы систему можно отобразить так:
( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c
n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Сделаем по аналогии такую же запись для вектора c ( 2 ) :
( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c
n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
И, далее действуя по тому же принципу, получаем:
( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c
n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Матричные равенства объединим в одно выражение:
c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c
n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )
Оно и будет определять связь векторов двух различных базисов.
Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :
e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e
n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )
Дадим следующие определения:
n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )
к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .
n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )
к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .
Видео:Как разложить вектор по базису - bezbotvyСкачать

11. Базис множества векторов и всего линейного пространства
Система векторов 


Все векторы системы 

Система векторов 
Любой вектор 


Если множество 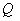


Числа 





Теорема (о единственности разложения по данному базису).
Разложение любого вектора 

Доказательство. Предположим, что для вектора 



Поскольку базисные векторы линейно независимы, то из полученного равенства следуют равенства 
Следствие. Любые два вектора равны тогда и только тогда, когда равны их координаты в каком – либо базисе.
Таким образом, при фиксированном базисе линейного пространства каждый вектор однозначно определяется своими координатами в этом базисе.
Теорема (о линейных свойствах координат векторов).
При сложении любых двух векторов их координаты в данном базисе складываются, а при умножении любого вектора на любое число координаты умножаются на это число.
Доказательство. Пусть любые два вектора 





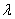


Отсюда и теоремы о единственности разложения векторов по данному базису следует истинность доказываемой теоремы.
Теорема о базисном миноре.
Базисные строки (столбцы) линейно независимы и образуют базис в системе всех строк (столбцов) произвольной матрицы 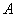
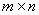
По определению базиса это означает, что любая строка или столбец матрицы могут быть представлены в виде линейной комбинации базисных строк или базисных столбцов, причем единственным образом. Все рассуждения достаточно провести для строк, так как, транспонировав исходную матрицу, мы получим доказательство для столбцов матрицы 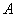
Линейную независимость базисных строк будем доказывать методом от обратного.
Пусть некоторые базисные строки линейно зависимы. Тогда одна из этих строк является линейной комбинацией остальных строк. Но тогда из свойств определителей следует, что базисный минор равен нулю. Базисный минор по определению не должен быть равен нулю. Таким образом, исходное предположение ложно и базисные строки линейно независимы.
Докажем теперь, что любая строка произвольной матрицы 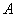
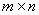
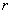
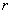
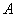
Пусть 
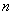
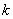
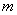

Равен нулю. Если 



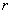




Алгебраические дополнения к элементам последнего столбца с номером 






Эти равенства справедливы для любых чисел 


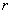
Из теоремы о базисном миноре вытекают два важных следствия.
1. Для любой матрицы число линейно независимых строк равно числу линейно независимых столбцов и равно рангу матрицы.
2. Определитель любого порядка равен нулю тогда и только тогда, когда его строки или его столбцы линейно зависимы.
Отметим, что по закону контрпозиции равносильное свойству 2 утверждение формулируется следующим образом: определитель отличен от нуля тогда и только тогда, когда его строки или его столбцы линейно независимы.
Покажем достаточность условия второго следствия. Если строки матрицы линейно зависимы, то по свойству системы зависимых векторов одна из строк является линейной комбинацией остальных строк. Вычитая из этой строки указанную линейную комбинацию, мы, не изменяя величины определителя, получим матрицу, содержащую нулевую строку. Определитель такой матрицы всегда равен нулю, что и требовалось доказать.
Покажем, что условие линейной зависимости столбцов квадратной матрицы является необходимым для равенства нулю определителя матрицы. Если определитель порядка 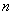
🎦 Видео
89. Разложение вектора по двум неколлинеарным векторамСкачать

9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

Базис. Разложение вектора по базису.Скачать

#вектор Разложение вектора по ортам. Направляющие косинусыСкачать

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

РАЗЛОЖЕНИЕ ВЕКТОРА ПО ДВУМ неколлинеарным ВЕКТОРАМ 9 классСкачать

РАЗЛОЖЕНИЕ ВЕКТОРА по трем векторамСкачать

Разложение вектора по двум неколлинеарным векторам | Геометрия 7-9 класс #85 | ИнфоурокСкачать

10 класс, 43 урок, Компланарные векторыСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Разложение вектора по векторамСкачать

Разложение вектора на неколлинеарные вектора.Скачать

Разложение вектора по трем некомпланарным векторамСкачать

Разложение вектора по двум неколлинеарным векторам. Урок 4. Геометрия 9 классСкачать

