Определение 1. Четырехугольник называют вписанным в окружность, если все вершины четырехугольника лежат на окружности.
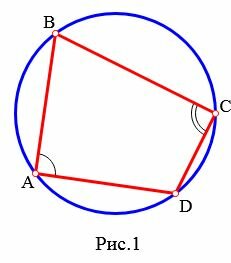
На рисунке 1 четырехугольник ABCD вписан в окружность. В этом случае говорят также, что окружность описан около четырехугольника.
 |
Теорема 1. Если четырехугольник вписан в окружность, то сумма противолежащих углов четырехугольника равна 180°.
Доказательство. Пусть четырехугольник ABCD вписан в окружность (Рис.1). Докажем, что 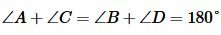
Углы A и C являются вписанными. Следовательно:
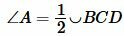 , , 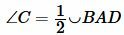 |
Но 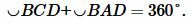
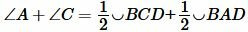 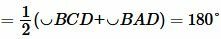 |
Аналогично можно показать, что 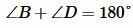
Заметим, что из 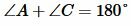
Как известно, вокруг любого треугольника можно описать окружность (см. статью Окружность, описанная около треугольника). Однако вокруг не каждого четырехугольника можно описать окружность. Например, если параллелограмм не является прямоугольником, то вокруг него не возможно описать окружность. Следующая теорема позволяет распознать четрехугольники, вокруг которых можно описать окружность.
Теорема 2. Если в четырехугольнике сумма противолежащих углов равна 180°, то около него можно описать окружность.
Доказательство. Пусть задан четырехугольник ABCD и пусть 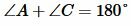
Предположим, что около этого четырехугольника невозможно описать окружность. Рассмотрим треугольник ABD и опишем окружность около этого треугольника (как отметили выше около любого треугольника можно описать окружность). Поскольку мы предположили, что у этого четырехугольника невозможно описать окружность, то точка C не принадлежит этой окружности. Поэтому эта точка лежит вне окружности или находится внутри окружности.
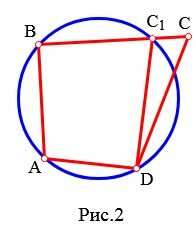  |
Случай 1. Точка C лежит вне описанной окружности (Рис.2).
Тогда сторона BC пересекает этот окружность. Обозначим эту точку C1. Четырехугольник ABC1D вписан в окружность. Тогда по теореме 1 имеем: 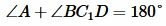
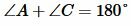
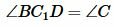
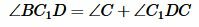
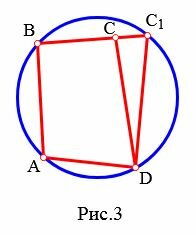
Случай 2. Точка C лежит внутри описанной окружности (Рис.3).
Проведем прямую BC и точку пересечения прямой и окружности обозначим C1. Получили четырехугольник ABC1D вписанный в окружность. Тогда по теореме 1 имеем: 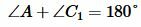
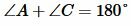
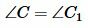
С другой стороны, угол C (т.е. угол BCD) является внешним углом треугольника DC1C, т.е. выполняется равенство 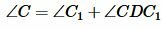
Следовательно точка C лежит на окружности.
Теорема 2 можно рассматривать метод определения принадлежности четырех точек одной окружности. Если четырехугольник вписан в окружность, то существует точка, равноудаленная от всех вершин четырехугольника (это центр окружности). Чтобы найти эту точку достаточно построить серединные перпендикуляры двух соседних сторон четырехугольника и найти точку их пересечения.
- Пересечения криволинейных поверхностей в начертательной геометрии с примером
- Проницание
- Врезание
- Одностороннее касание
- Двойное касание
- Пересечение поверхностей второго порядка
- Теорема о двойном касании
- Теорема Монжа
- Теорема монжа о вписанном четырехугольнике
- §3. Свойства касательных, хорд, секущих. Вписанные и описанные четырёхугольники
- 🔍 Видео
Видео:Вебинар 5. ОММО. Теорема Монжа. Последовательности. Вписанные углы.Скачать

Пересечения криволинейных поверхностей в начертательной геометрии с примером
Содержание:
Возможные случаи пересечения криволинейных поверхностей:
Существуют четыре варианта пересечения двух поверхностей.
Видео:#58. Олимпиадная задача о четырехугольникеСкачать

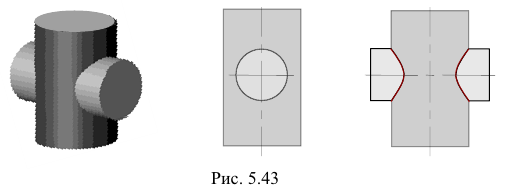
Проницание
Все образующие первой поверхности (цилиндра) пересекаются со второй поверхностью, но не все образующие второй поверхности пересекаются с первой. В этом случае линия пересечения поверхностей распадается на две замкнутые кривые линии (рис. 5.43).
Видео:Теорема Монжа и задача со Всеросса | Олимпиадная математикаСкачать

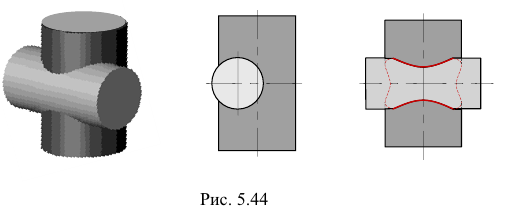
Врезание
Не все образующие той и другой поверхности пересекаются между собой. В этом случае линия пересечения — одна замкну тая кривая линия (рис. 5.44).
Видео:Теоремы об окружностях для четырехугольниковСкачать

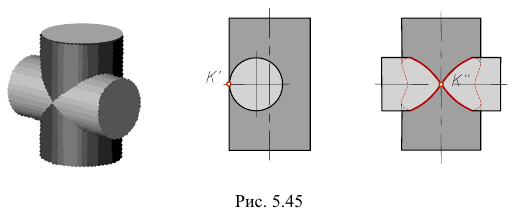
Одностороннее касание
Все образующие одной поверхности пересекаются со второй, но не все образующие второй поверхности пересекаются с первой. Поверхности имеют в одной точке (точка К на рис. 5.45) общую плоскость касания. Линия пересечения распадается на две замкнутые кривые линии, пересекающиеся в точке касания.
Видео:Теорема Птолемея - одна из самых мощных теорем планиметрии. На нее бывают задачи в ЕГЭСкачать

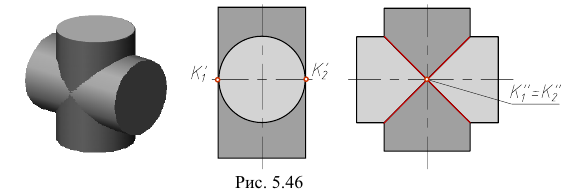
Двойное касание
Все образующие обеих поверхностей пересекаются между собой. Пересекающиеся поверхности имеют две общие касательные плоскости. В этом случае линия пересечения распадается на две плоские кривые, которые пересекаются в точках касания (рис. 5.46).
Пересечение поверхностей второго порядка
В общем случае две поверхности второго порядка пересекаются по пространственной кривой четвертого порядка. Следует отметить, что при некоторых особых положениях относительно друг друга поверхности второго порядка могут пересекаться по плоским кривым второго порядка, то есть пространственная кривая пересечения распадается на две плоские кривые.
Теорема о двойном касании
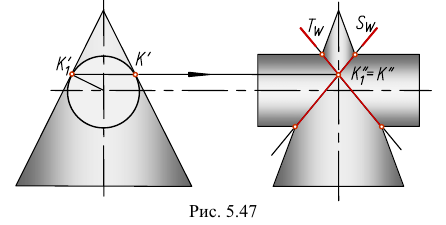
Если две поверхности второго порядка имеют две общие точки (точки касания), то линия их взаимного пересечения распадается на две плоские кривые второго порядка. Причем плоскости этих кривых пройдут через прямую, соединяющую точки касания.
На рис. 5.47 показано построение линии пересечения поверхностей прямого кругового цилиндра и эллиптического конуса. Линии пересечения — эллипсы — лежат в профильно-проецирующих плоскостях S и Т, проходящих через прямую 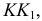
Теорема Монжа
Если две поверхности второго порядка описаны около третьей поверхности второго порядка или вписаны в нее, то линия их взаимного пересечения распадается на две плоские кривые. Плоскости этих кривых пройдут через прямую, соединяющую точки пересечения линий касания.
Если оси пересекающихся поверхностей вращения параллельны какой — либо плоскости проекций, то на эту плоскость кривые линии проецируются в прямые.
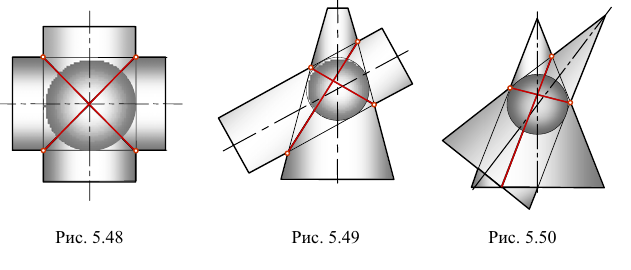
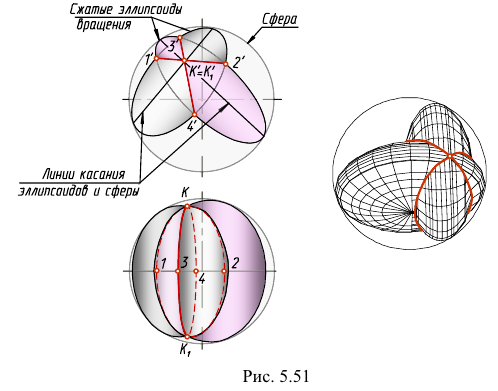
На рис. 5.48 — 5.50 приведены примеры построения линий пересечения поверхностей на основании теоремы Монжа, где два цилиндра, цилиндр и конус и два конуса описаны вокруг сферы, а на рис. 5.51 приведен пример построения линии пересечения двух сжатых эллипсоидов вращения, вписанных в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Пересечения поверхностей с прямой и плоскостью
- Взаимное пересечение поверхностей
- Собственные тени поверхностей вращения
- Построение падающих теней
- Взаимное положение прямой и плоскости
- Решение метрических задач
- Тени в ортогональных проекциях
- Кривые поверхности
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:11 класс, 43 урок, Вписанный четырехугольникСкачать

Теорема монжа о вписанном четырехугольнике
§3. Свойства касательных, хорд, секущих. Вписанные и описанные четырёхугольники
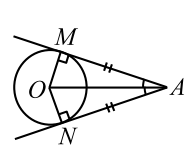 |
| Рис. 17 |
Если из точки к окружности проведены две касательные, то длины отрезков от этой точки до точек касания равны и прямая, проходящая через центр окружности и эту точку, делит угол между касательными пополам (рис. 17).
Используя это свойство, легко решить следующую задачу.
На основании $$ AC$$ равнобедренного треугольника $$ ABC$$ расположена точка $$ D$$ так, что $$ AD=a,CD=b$$. Окружности, вписанные в треугольники $$ ABD$$ и $$ DBC$$, касаются прямой $$ BD$$ в точках $$ M$$ и $$ N$$ соответственно. Найти отрезок $$ MN$$.
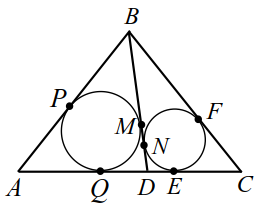 | 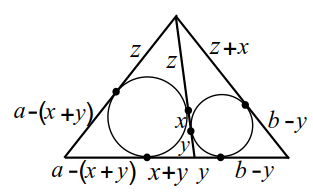 |
| Рис. 18 | Рис. 18a |
$$ DE=y$$, $$ QD=x+y$$, $$ AQ=AP=a-(x+y)$$, $$ EC=CF=b-y$$, $$ PB=BM=z, BF=BN=z+x$$ (рис. 18а). Выразим боковые стороны:
$$ AB=z+a-x-y$$, $$ BC=z+x+b-y$$. По условию $$ AB=BC$$; получим
Четырёхугольник называется описанным около окружности, если окружность касается всех его сторон.
В выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда суммы длин противолежащих сторон равны.
 |
| Рис. 19 |
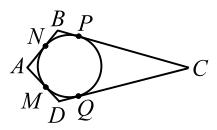
Пусть четырёхугольник $$ ABCD$$ описан около окружности (рис. 19).
По свойству касательных: $$ AM=AN$$, $$ NB=BP$$, $$ PC=CQ$$ и $$ QD=DM$$, поэтому
$$ AM+MD+BP+PC=AN+NB+CQ+QD$$, что означает
Докажем обратное утверждение. Пусть в выпуклом четырёхугольнике $$ ABCD$$ стороны удовлетворяют условию $$ AB+CD=BC+AD.$$ Положим $$ AD=a, AB=b, BC=c, CD=d.$$
По условию $$ a+c=b+d,$$ что равносильно $$ c-b=d-a.$$
Пусть $$ d>a.$$ Отложим на большей стороне $$ CD$$ меньшую сторону `DM=a` (рис. 20). Так как в этом случае $$ c>b$$, то также отложим $$ BN=b$$, получим три равнобедренных треугольника `ABN`, `ADM` и `MCN`.
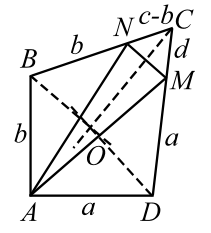 |
| Рис. 20 |
В равнобедренном треугольнике биссектриса угла при вершине является медианой и высотой, отсюда следует, что если провести биссектрисы углов `B`, `C` и `D`, то они разделят пополам соответственно отрезки `AN`, `MN` и `AM` и будут им перпендикулярны. Это означает, что биссектрисы будут серединными перпендикулярами трёх сторон треугольника $$ ANM$$, а они по теореме пересекаются в одной точке. Обозначим эту точку $$ O$$. Эта точка одинаково удалена от отрезков `AB` и `BC` (лежит на $$ OB$$), `BC` и `CD` (лежит на $$ OC$$) и `CD` и `AD` (лежит на $$ OD$$), следовательно, точка $$ O$$ одинакова удалена от всех четырёх сторон четырёхугольника $$ ABCD$$ и является центром вписанной окружности. Случай $$ d=a$$, как более простой, рассмотрите самостоятельно.
Равнобокая трапеция описана около окружности. Найти радиус окружности, если длины оснований равны $$ a$$ и $$ b$$.
 |
| Рис. 21 |
Пусть в равнобокой трапеции $$ ABCD$$ `BC=b`, `AD=a` (рис. 21). Эта трапеция равнобокая $$ (AB=CD)$$, она описана около окружности, следовательно, $$ AB+CD=AD+BC$$ Отсюда получаем:
Проведём $$ BM$$ и $$ CN$$ перпендикулярно $$ AD$$. Трапеция равнобокая, углы при основании равны, следовательно, равны и треугольники $$ ABM$$ и $$ DCN$$ и $$ AM=ND$$. По построению $$ MBCN$$ — прямоугольник, $$ MN=BC=b$$ поэтому $$ AM=<displaystyle frac>(AD-BC)-<displaystyle frac>(a-b)$$. Из прямоугольного треугольника $$ ABM$$ находим высоту трапеции $$ ABCD$$:
Очевидно, что высота трапеции равна диаметру окружности, поэтому
радиус вписанной окружности равен $$ overline<)r=<displaystyle frac>sqrt>$$.
Очень полезная задача. Заметим, что из решения также следует, что в равнобокой описанной трапеции $$ overline<)mathrmalpha =<displaystyle frac>>$$.
Градусная мера угла, образованного хордой и касательной, имеющими общую точку на окружности, равна половине градусной меры дуги, заключённой между его сторонами (рис. 22).
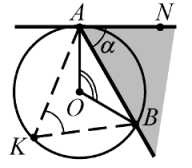 |
| Рис. 22 |
Рассматриваем угол $$ NAB$$ между касательной $$ NA$$ и хордой $$ AB$$. Если $$ O$$ — центр окружности, то $$ OAperp AN$$, `/_OAB=/_OBA=90^@alpha`. Сумма углов треугольника равна `180^@`, следовательно, $$ angle AOB=2alpha $$. Итак, $$ alpha =angle NAB=<displaystyle frac>angle AOB.$$
Обратим внимание, что угол $$ NAB$$ равен любому вписанному углу $$ AKB$$, опирающемуся на ту же дугу $$ AB$$.
Случай `/_alpha>=90^@` рассматривается аналогично.
Из этого свойства следует важная теорема «о касательной и секущей», которая часто используется при решении задач.
Пусть к окружности проведены из одной точки касательная $$ MA$$ и секущая $$ MB$$, пересекающая окружность в точке $$ C$$ (рис. 23). Тогда справедливо равенство
т. е. если из точки `M` к окружности проведены касательная и секущая, то квадрат отрезка касательной от точки `M` до точки касания равен произведению длин отрезков секущей от точки `M` до точек её пересечения с окружностью.
Угол $$ MAC$$ образован хордой и касательной, $$ angle MAC=angle ABC$$. Так как в треугольниках $$ MAC$$ и $$ MBA$$ угол $$ M$$ общий, то по двум углам они подобны. Из подобия следует:
 |
| Рис. 23 |
Если из точки $$ M$$ к окружности проведены две секущие: $$ MB$$, пересекающая окружность в точке $$ C$$ и $$ MK$$, пересекающая окружность в точке $$ L$$ (рис. 23), то справедливо равенство $$ MB·MC=MK·ML$$.
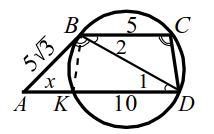 |
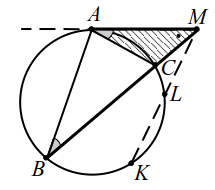
| Рис. 24 |
Окружность проходит через вершины $$ C u D$$ трапеции $$ ABCD,$$ касается боковой стороны $$ AB$$ в точке $$ B$$ и пересекает большее основание $$ AD$$ в точке $$ K$$ (рис. 24). Известно, что $$ AB=5sqrt$$, $$ BC=5$$ и $$ KD=10$$.
Найти радиус окружности.
1. Пусть $$ AK=x$$ тогда $$ AD=10+x$$ю
По теореме о касательной и секущей:
$$ A^=AK·KD$$ т. е. $$ 75=x(x+10)$$, откуда $$ x=5$$. Итак $$ AD=15$$.
2. Заметим теперь, что угол $$ ABD$$ между касательной $$ AB$$ и хордой $$ BD$$ равен вписанному углу $$ BCD$$, а из параллельности прямых $$ AD$$ и $$ BC$$ следует равенство углов `1` и `2`. По первому признаку подобия $$ △ABDsim △DCB$$. Из подобия имеем $$ <displaystyle frac>=<displaystyle frac><displaystyle frac>$$. Из последнего равенства находим, что $$ B^=AD·BC$$, т. е. $$ BD=sqrt=5sqrt$$, а из первого равенства находим $$ CD=<displaystyle frac>=5$$.
3. Так как $$ KB=CD$$ ($$ KBCD$$ — вписанная трапеция, она равнобокая), и $$ K^+B^=K^,$$ то `/_ KBD=90^@` и $$ KD$$ — диаметр окружности.
Значит, её радиус равен `5`.
Около четырёхугольника можно описать окружность тогда и только тогда, когда сумма противолежащих углов равна `180^@`.
Из этой теоремы следует:
a) из всех параллелограммов только около прямоугольника можно описать окружность;
б) около трапеции можно описать окружность только тогда, когда она равнобокая.
 |
| Рис. 25 |
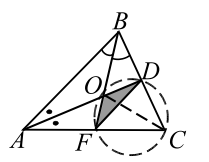
В треугольнике $$ ABC$$ биссектрисы $$ AD$$ и $$ BF$$ пересекаются в точке $$ O$$ (рис. 25). Известно, что точки $$ F, O, D$$, и `C` лежат на одной окружности и что $$ DF=sqrt.$$ Найти площадь треугольника $$ ODF$$.
Четырёхугольник $$ DOFC$$ вписан в окружность, по теореме 9:
$$ angle DOF=pi -angle C$$, т. е. $$ pi -<displaystyle frac>(angle A+angle B)=pi -angle C$$, откуда, учитывая, что $$ angle A+angle B+angle C=pi $$, находим $$ angle С=<displaystyle frac>$$.
Теперь заметим, что $$ O$$ — точка точка пересечения биссектрис, $$ CO$$ — биссектриса угла $$ C,$$ следовательно, углы $$ OCD$$ и $$ OCF$$ равны друг другу. Это вписанные углы, поэтому вписанные углы $$ ODF$$ и $$ OFD$$ равны им и равны друг другу. Таким образом,
Треугольник $$ DOF$$ равнобедренный с основанием $$ DF=sqrt$$ и углом при основании `30^@`. Находим его высоту, опущенную из вершины $$ O$$ и площадь треугольника $$ ODF: S=<displaystyle frac>h·DF=<displaystyle frac<sqrt>>$$.
🔍 Видео
Вписанные четырехугольники. 9 класс.Скачать

3 правила для вписанного четырехугольника #shortsСкачать

Теорема Монжа.Скачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

Формула Брахмагупты. Площадь вписанного четырехугольника.Скачать

Вписанная и описанная окружность - от bezbotvyСкачать

ЕГЭ 2022 Планиметрия Теорема Птолемея. Вписанный четырёхугольникСкачать

Вписанный в окружность четырёхугольник.Скачать

8 класс, 34 урок, Теорема о вписанном углеСкачать

8 класс, 3 урок, ЧетырехугольникСкачать

Свойство и признак вписанного четырехугольникаСкачать

Вписанный четырёхугольник | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис ТрушинСкачать

#213. Теоремы Монжа | Брианшона | ДезаргаСкачать