Напряженность электростатического поля зависит от свойств среды (от с). Кроме того, вектор напряженности Е на границе диэлектриков претерпевает скачкообразное изменение. Введем для описания электрического поля системы зарядов с учетом поляризационных свойств диэлектриков вспомогательный вектор, использование которого во многих случаях упрощает изучение поля в диэлектриках.
Внутри диэлектрика поле определяется и сторонними, и связанными зарядами. Поэтому, исходя из теоремы Гаусса для вектора напряженности в вакууме (12.11) и учитывая величину плотности нескомпенсированного связанного заряда р’ в диэлектрике, запишем:
По теореме Гаусса для вектора поляризации (13.5)
Тогда имеем, что
где вектором электрического смещения (электрической индукции) называется вектор
Для изотропного диэлектрика с учетом формулы (13.3) получаем
Единица вектора электрического смещения в СИ — кулон на метр в квадрате (Кл/м 2 ).
Вектор D описывает электростатическое поле, создаваемое сторонними зарядами в вакууме, но при таком их распределении в пространстве, какое имеется при наличии диэлектрика.
Аналогично линиям напряженности можно ввести линии электрического смещения. Направление и густота линий вектора электрического смещения определяются так же, как и для вектора напряженности Е.
Согласно уравнению (13.11), теорема Гаусса в дифференциальной форме для вектора D имеет вид
т.е. дивергенция поля вектора D равна объемной плотности стороннего заряда в той же точке.
- Теорема Гаусса в присутствии диэлектриков
- Теорема Остроградского-Гаусса
- Теорема Остроградского-Гаусса в дифференциальной форме
- Теорема Остроградского-Гаусса для диэлектриков
- Теорема гаусса вектор d
- Теорема Гаусса для вектора P
- Вектор D
- Условия на границе двух диэлектриков
- Поле внутри однородного изотропного диэлектрика
- 🔥 Видео
Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Теорема Гаусса в присутствии диэлектриков
Влияние диэлектриков на электрическое поле сводится к ответному действию возникающих в поле поляризационных зарядов. Теорема Остроградского-Гауса для тел в вакууме электростатического поля может быть трансформирована с помощью добавления к свободным зарядам поляризационных для получения теоремы с диэлектриками. В этом случае она запишется как:
Со значением q j s υ в качестве связанных зарядов, q i — свободных зарядов, Φ E — потока вектора напряженности электрического поля.
Видео:44. Электрическое поле в диэлектрике. Вектор поляризованностиСкачать

Теорема Остроградского-Гаусса
Если использовать вектор электрического смещения D → , то это заметно облегчает анализ поля при наличии диэлектрика. Теорему Остроградского-Гаусса при наличии диэлектрика можно записать в интегральном виде:
∮ S D → · d S → = ∑ i = 1 N q i = Q , где Q является суммарным свободным зарядом, находящийся внутри объема, который ограничен поверхностью S .
Поток вектора D → через замкнутую поверхность может быть определен только с помощью свободных зарядов. В вакууме векторы D → и E → совпадающие.
Дифференциальная форма теоремы Гаусса выражения ∮ S D → · d S → = ∑ i = 1 N q i = Q изображается как:
d i v D → = ρ с ρ , являющейся объемной плотностью свободных зарядов.
Теорема Остроградского-Гаусса вида ∮ S D → · d S → = ∑ i = 1 N q i = Q и d i v D → = ρ справедлива только в электростатике и выполняется для переменных полей. Ее относят к составной части системы уравнений Максвелла.
Видео:Билет №02 "Теорема Гаусса"Скачать

Теорема Остроградского-Гаусса в дифференциальной форме
Напомним формулу вектора электрической индукции:
D → = ε 0 E → + P → со значением ε 0 в качестве электрической постоянной, E → — вектора напряженности, P → — вектора поляризации.
Произведем подстановку формулы D → = ε 0 E → + P → в d i v D → = ρ :
d i v D → = d i v ε 0 E → + P → = ε 0 d i v E → + d i v P → .
При использовании теоремы Остроградского-Гаусса дифференциального вида, получим:
d i v E → = 1 ε 0 ρ — d i v P → .
Для вектора напряженности вышеуказанная формула примет вид в присутствии диэлектрика:
d i v E → = 1 ε 0 ρ + ρ s v с ρ s v , являющейся плотностью заряда. В этом случае необходимо применить d i v E → = 1 ε 0 ρ + ρ s v и d i v E → = 1 ε 0 ρ — d i v P → :
d i v P → = — 1 ε 0 c s v .
Видео:Физический кружок: теорема Гаусса, диэлектрики | Второе занятиеСкачать

Теорема Остроградского-Гаусса для диэлектриков
Теорема Остроградского-Гаусса для вектора электрического смещения в диэлектрике выглядит также, как и для напряженности поля в вакууме. Отсюда следует, что математические соотношения, получившиеся для E → поля в вакууме, аналогичны записям для однородного диэлектрика при замене напряженности электрического поля на вектор D → .
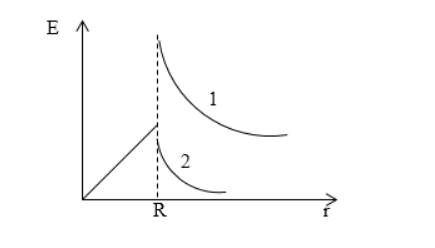
Дан диэлектрический шар, имеющий диэлектрическую проницаемость ε 1 , равномерно заряжен по объему с постоянной плотностью заряда ρ . Его нахождение в среде обусловлено наличием диэлектрической проницаемости ε 2 . Изобразить график напряженности поля шара от расстояния до его центра.
Решение
Поле, создаваемое шаром по заданным условиям, имеет сферическую симметрию. Необходимо рассмотреть его внутри шара r ≤ R . Для нахождения E ( r ) выбирается сферическая поверхность с радиусом меньше сферы. По теореме Остроградского-Гаусса:
E · S = q ε 1 ε 0 , где S — площадь поверхности сферы, которая была выделена. Отсюда следует:
Заряд, находящийся внутри сферы, ищем из формулы:
q = ρ V = ρ 4 3 π r 3 .
Очевидно, что будут происходить изменения напряженности поля внутри шара r ≤ R , согласно выражениям:
E · 4 π r 2 = ρ 4 3 π r 3 ε 1 ε 0 ,
E = ρ r 3 ε 1 ε 0 .
Перейдем к рассмотрению поля вне шара r ≥ R . Для нахождения E ( r ) выбираем сферическую поверхность с радиусом больше радиуса сферы. По теореме Остроградского-Гаусса получим:
E · S = q ε 2 ε 0 , где S обозначает площадь поверхности выделенной сферы. Отсюда следует:
Формула S = 4 π r 2 имеет r ≥ R . Поэтому находящийся внутри заряд выделенной сферы находится из:
q = ρ V = ρ 4 3 π R 3 .
Далее следует подставить площадь из S = 4 π r 2 , заряд из q = ρ V = ρ 4 3 π R 3 , подставив в E · S = q ε 2 ε 0 :
E · 4 πr 2 = ρ 4 3 πR 3 ε 2 ε 0 .
E = ρ R 3 3 ε 2 ε 0 r 2 .
В результате запишем:
E = ρ r 3 ε 1 ε 0 п р и r ≤ R , E = ρ R 3 3 ε 2 ε 0 r 2 п р и r ≥ R .
Ответ: графики показаны на рисунке 1 . Внутри шара напряженность увеличивается прямо пропорционально расстоянию от центра шара. Вне шара она равняется E
1 r 2 . На границе диэлектриков происходит разрыв. Кривая под номером 1 соответствует условию ε 1 > ε 2 .
Предположим, что имеется воображаемая сфера, в центре которой находится точечный заряд. Будет ли изменяться поток вектора напряженности через эту поверхность, если: 1 ) все пространство будет заполнено однородным и изотопным диэлектриком, 2 ) произвести замену сферической поверхности на кубическую?
Решение
- По теореме Остроградского-Гаусса поток вектора напряженности через поверхность сферы в пространстве с диэлектриком будет равняться:
Φ E = ∮ S E → d S → = 1 ε 0 q + ∑ j = 1 K q j s v , со значением q j s v в качестве связанных зарядов, которые вызваны поляризацией диэлектрика полем одиночного заряда, q в качестве свободного заряда, находящегося в центре сферы.
Учитывая теорему Остроградского-Гаусса, формула потока вектора напряженности через поверхность сферы в пространстве без диэлектрика примет вид:
Φ E = ∮ S E → d S → = 1 ε 0 q .
- Поле было создано при помощи точечного свободного заряда, то при замене формы поверхности потока вектор напряженности не будет изменяться, потому как равняется аналогичным значению заряда, находящегося на поверхности.
Видео:ЧК_МИФ 3_1_5_3_(L3) ИСПОЛЬЗОВАНИЕ т.ГАУССА ДЛЯ ВЕКТОРА DСкачать

Теорема гаусса вектор d
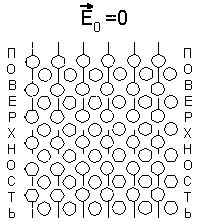
Диэлектрики — это вещества, которые практически не проводят электрический ток. Поведение диэлектриков в электрическом поле определяется их внутренним строением. Как известно, мельчайшей частицей вещества, сохраняющей его химические свойства, является молекула. Молекулы состоят из атомов, в состав которых входят положительно заряженные ядра и отрицательно заряженные электроны. В целом молекулы нейтральны. Согласно теории ковалентных связей устойчивость молекул достигается путем образования одной или нескольких пар электронов, которые становятся общими для соединяющихся атомов, т. е. входят одновременно в состав оболочек двух атомов.
Для каждого рода зарядов — положительных (ядер) и отрицательных (электронов) — можно найти такую точку, которая будет являться как бы их «электрическим центром тяжести». Эти точки называются полюсами молекулы. Если в молекуле электрические центры тяжести положительных и отрицательных зарядов совпадут, то молекула будет неполярной . Но если молекула построена несимметрично, например состоит из двух разнородных атомов, то общая пара электронов может быть в большей или меньшей степени смещена в сторону одного из атомов. Очевидно, что в этом случае, вследствие неравномерного распределения положительных и отрицательных зарядов внутри молекулы, их электрические центры тяжести не совпадут и получится молекула, называемая полярной .
Для описания макроскопических электрических свойств диэлектриков достаточно ограничиться представлением о том, что в них отсутствуют свободные носители заряда, и при помещении диэлектрика в электрическое поле в материале возбуждается множество микроскопических диполей. В случае неполярных молекул это происходит путем смещения в пределах молекул их положительных зарядов в направлении внешнего поля и отрицательных в противоположном направлении (рис. 5.1).
 | 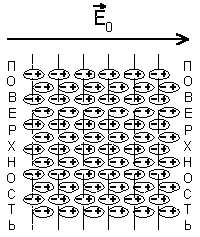 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
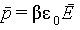 | (5.1) |
где коэффициент пропорциональности β называется поляризуемостью молекулы.
Для вещества, состоящего из полярных молекул, под действием момента сил (3.9) происходит преимущественное выстраивание молекул в направлении внешнего поля. В обоих случаях (неполярных и полярных молекул) в результате появляется дипольный момент и у всего объема диэлектрика. Средний дипольный момент, индуцированный полем в единице объема, называется поляризованностью диэлектрика:
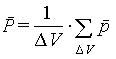 | (5.2) |
где суммирование производится по всем молекулам, находящимся в объеме Δ V, а дипольный момент p каждой молекулы определяется суммированием по всем заряженным частицам, входящим в молекулу:
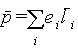 | (5.3) |
где ei — заряд каждой частицы, а li — ее смещение под действием электрического поля.
Домножив и разделив правую часть (5.2) на число молекул Δ N, находящихся в объеме Δ V, получим еще одно выражение для поляризованности:
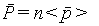 | (5.4) |
где n = Δ N / Δ V — концентрация молекул, а — средний диполный момент молекулы.
Вообще говоря, P меняется в диэлектрике от точки к точке, но для широкого класса веществ в каждой точке P
E. Существуют вещества, обладающие поляризованностью и в отсутствие внешнего поля, однако здесь они не рассматриваются.
Поскольку в целом молекулы нейтральны, то именно дипольный момент и определяет электрическое поле, создаваемое самим материалом, когда его помещают во внешнее поле. В силу принципа суперпозиции поле внутри диэлектрика есть сумма внешнего поля и поля от всех диполей, индуцированных в диэлектрике:
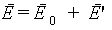 | (5.5) |
где E0 — напряженность поля сторонних зарядов, а E’ — связанных зарядов. Связанными зарядами называются нескомпенсированные заряды, появляющиеся в результате поляризации молекул диэлектрика, тогда как сторонними — свободные заряды, находящиеся в диэлектрике или вне его. E0 и E’ представляют собой макрополя, т.е. усредненные по некоторому малому объему микрополя, создаваемые сторонними и связанными зарядами, соответственно.
Так как каждая молекула поляризуется под воздействием как поля сторонних зарядов, так и поля, создаваемого всеми другими поляризованными молекулами, то поляризованность диэлектрика пропорциональна напряженности именно суммарного поля (5.5):
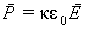 | (5.6) |
где греческой буквой «каппа» обозначена, так называемая, диэлектрическая восприимчивость. Для изотропных диэлектриков κ — просто коэффициент, и векторы P и E в этом случае совпадают по направлению. В общем случае это не так. Заметим, что пропорциональность поляризованности напряженности поля имеет место для широкого класса диэлектриков, однако существуют вещества (сегнетоэлектрики) для которых зависимость P от E имеет гораздо более сложный характер, чем (5.6). Здесь они не рассматриваются.
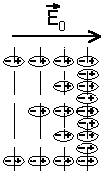 | При поляризации однородного диэлектрика (см. рис. 5.1) смещения зарядов внутри любого выбранного слоя внутри диэлектрика происходят таким образом, что количество связанного заряда, покидающего слой, равно заряду, входящему в него. Таким образом объемный заряд внутри диэлектрика не образуется. В поверхностных же слоях образуется связанный поверхностный заряд . В случае же неоднородного диэлектрика в каждый слой, мысленно выделенный внутри материала, с одной стороны входит больше заряда, чем выходит с другой, и связанный заряд образуется не только на поверхности, но и в объеме диэлектрика, как это показано на рис. 5.2. |
Теорема Гаусса для вектора P
Выделим внутри диэлектрика некоторый объем V, ограниченный поверхностью S. Подсчитаем, сколько заряда проходит через элемент dS воображаемой поверхности, когда материал поляризуется. При появлении электрического поля положительные заряды молекул сместятся на некоторое расстояние вдоль поля, а отрицательные — в противоположном направлении. При этом каждая молекула приобретет дипольный момент, определяемый соотношением (5.3), причем вектор смещения будет направлен вдоль поля, а средняя длина вектора смещения l для диполей, находящихся в прилегающем к dS слою, будет согласно (5.4) связана с поляризацией этого слоя соотношением
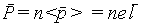 | (5.7) |
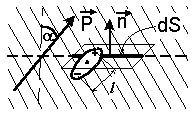 | Элемент поверхности dS пересечет все те диполи, центры которых расположены в прилегающем к нему слое толщины l | cos α| , где α — угол между нормалью к dS и направлением вектора поляризованности (рис. 5.3). Объем этого слоя равен l | cos α| dS, а число пересекаемых элементом dS диполей равно n l | cos α| dS. |
Следовательно, для выбранного элемента поверхности соответствующая абсолютная величина нескомпенсированного заряда внутри объема V равна
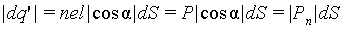 | (5.8) |
При этом, если cos α > 0, то снаружи от элемента dS находятся положительные заряды, а внутри — отрицательные, а если cos α Тогда поток вектора P через поверхность S, ограничивающую объем V, связан с полным связанным зарядом q‘ в объеме соотношением
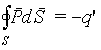 | (5.9) |
Последнее соотношение представляет собой теорему Гаусса для вектора P .
Преобразуем левую часть выражения (5.9) по теореме Остроградского-Гаусса, а связанный заряд q’ представим, как
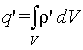 | (5.10) |
где ρ ‘ — объемная плотность связанного заряда.
Тогда будем иметь
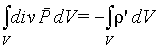 | (5.11) |
откуда с учетом произвольности выбранного объема V получим теорему Гаусса для вектора поляризованности в дифференциальной форме:
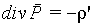 | (5.12) |
Выясним, в каких случаях объемная плотность связанных зарядов отлична от нуля. Выразим P в (5.12) через E согласно (5.6)
| ρ ‘ = – ∇(κεo E) = – εo∇(κ E) = – εo( E ∇κ + κ∇ E) | (5.13) |
В теореме Гаусса для вектора E, записанной в дифференциальной форме (2.17), в правой части стоит объемная плотность заряда, включающая в случае диэлектрика как плотность сторонних, так и связанных зарядов
| ∇ E=( ρ + ρ ‘)/ εo | (5.14) |
Заменяя в (5.13) ∇E согласно (5.14) получим
| ρ ‘ = – εo E ∇κ – κρ – κρ ‘ | (5.15) |
| ρ ‘ = – (εo E ∇κ + κρ )/(1+ κ) | (5.16) |
Из последнего выражения видно, что объемная плотность связанного заряда в диэлектрике отлична от нуля в двух случаях: (1) когда диэлектрик поляризуется неоднородно ( κ есть функция координаты) и/или (2) в диэлектрике присутствует сторонний заряд ( ρ отлично от нуля). При однородной поляризации и отсутствии стороннего заряда внутри диэлектрика равенство нулю связанного объемного заряда легко усматривается из рис. 5.1.
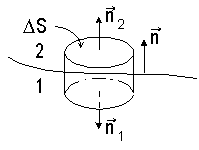 | Рассмотрим границу раздела двух однородных изотропных диэлектриков 1 и 2 (рис. 5.4). Выделим мысленно на границе раздела цилиндр с площадью основания Δ S с образующей, перпендикулярной границе раздела. Выберем произвольно направление нормали n к границе, как показано на рисунке. Пусть площадка Δ S, вырезаемая цилиндром на границе, столь мала, что ее можно считать плоской, а поляризованность каждого из диэлектриков в ее пределах постоянной. |
Найдем поток Ф вектора P через поверхность цилиндра. Поток через нижнее основание цилиндра равен P1· Δ S cos (P1, n1), а через верхнее P2· Δ S cos (P2, n2), где индексами 1 и 2 обозначены величины, относящиеся соответственно к внутренней и внешней по отношению к нормали n сторонам границы раздела. Поток через боковую поверхность цилиндра обозначим Ф’. Тогда будем иметь
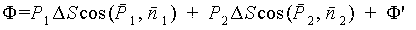 | (5.17) |
Направление нормали n2 совпадает с направлением нормали n, а направление нормали n1 прямо противоположно. Следовательно
| P1· Δ S cos (P1, n1) = —P1n ; | P2· Δ S cos (P2, n2)=P2n , |
где P1n и P2n — проекции вектров P1и P2 на нормаль n. Таким образом
Будем теперь уменьшать высоту цилиндра, не изменяя при этом его основания. Поток Ф’ через безгранично уменьшающуюся боковую поверхность будет стремиться к нулю, так что общий поток через поверхность цилиндра сведется в пределе к потоку через его основания:
Для однородных диэлектриков объемный связанный заряд, как было показано выше, равен нулю. Стало быть внутри цилиндра окажется заряд, расположенный на границе раздела на элементе поверхности Δ S. Этот заряд равен Δ S · σ ‘, где σ ‘ — поверхностная плотность связанного заряда на границе раздела диэлектриков. На основании теоремы Гаусса для вектора P запишем
| (P2n — P1n ) = — σ ‘ | (5.18) |
Иными словами, на границе раздела нормальная составляющая вектора P испытывает разрыв, величина которого зависит от σ ‘. В частности, если среда 2 вакуум, то P2n = 0 и
| Pn = σ ‘ | (5.19) |
где Pn проекция вектора P на внешнюю нормаль к поверхности данного диэлектрика.
Вектор D
В случае диэлектрика теорема Гаусса для вектора E запишется как
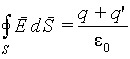 | (5.20) |
где q и q‘ — находящиеся внутри поверхности S полные сторонний и связанный заряды, соответственно. Поскольку связанный заряд в диэлектрике индуцируется под воздействием искомого поля E, то применение теоремы Гаусса в виде (5.20) для определения напряженности поля становится практически невозможным. Для преодоления указанной трудности вводится вспомогательный вектор D. Логика определения этого вектора вытекает из следующих соображений. Выразим связанный заряд в (5.20) согласно (5.9)
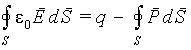 | (5.21) |
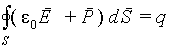 | (5.22) |
Как видно из (5.22) если ввести вспомогательный вектор в виде D = ε 0E + P , то его поток будет определяться только сторонним зарядом, распределение которого предполагается известным. Тогда для вектора D теорема Гаусса имеет вид
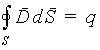 | (5.23) |
Пользуясь теми же соображениями, что и при переходе от интегральной формы теоремы Гаусса для вектора P к дифференциальной, запишем теорему Гаусса для вектора D в дифференциальной форме
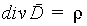 | (5.24) |
Для изотропного диэлектрика P = κε 0E. Тогда
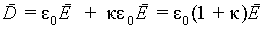 | (5.25) |
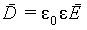 | (5.26) |
где обозначено ε = 1+ κ — диэлектрическая проницаемость вещества. Для всех диэлектриков ε > 0. Для вакуума ε = 1.
Условия на границе двух диэлектриков
Рассмотрим поведение векторов E и D на границе раздела однородных изотропных диэлектриков.
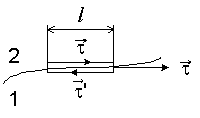 | Для установления связи между тангенциальными составляющими вектора E по обе стороны границы воспользуемся теоремой о циркуляции вектора E. Выберем контур небольшой длины l, как показано на рис. 5.5 и в предположении, что векторы E1 и E2 с обеих сторон границы постоянны в пределах контура, запишем на основании этой теоремы |
| E2 τ + E1 τ ‘ + C’ = 0 | (5.27) |
где проекции вектора E взяты в непосредственной близости от границы раздела на направление обхода контура, указанное на рисунке стрелками, а C’ — вклад в циркуляцию от перпендикулярных к границе сторон контура. В пределе при стремящейся к нулю высоте контура этим вкладом можно пренебречь и тогда
| E2 τ + E1 τ ‘ = 0 | (5.28) |
Если внутри диэлектрика 1 проекцию вектора E взять не на орт τ ‘, а на общий орт τ , то так как E1 τ ‘ = -E1 τ , то получим
| E2 τ — E1 τ = 0 | (5.29) |
| E2 τ = E1 τ | (5.30) |
Иными словами, тангенциальная составляющая вектора E одинакова по обе стороны границы раздела.
Заменив согласно (5.26) проекции вектора E проекциями вектора D, деленными на εoε , получим
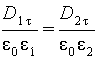 | (5.31) |
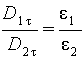 | (5.32) |
Обратимся теперь к нормальной составляющей вектора D. Воспользуемся для этого теоремой Гаусса для этого вектора. Выбирая поверхность интегрирования как показано на рис. 5.4 и следуя тем же рассуждениям, которые привели к выражению (5.18), получим
| D2n — D1n= σ | (5.33) |
Из этого соотношения следует, что при наличии на границе раздела стороннего заряда с поверхностной плотностью σ нормальная составляющая вектора D терпит разрыв. При отсутствии стороннего заряда на границе
| D1n = D2n | (5.34) |
Нормальные составляющие вектора E с разных сторон границы раздела относятся тогда на основании (5.26) , как
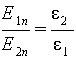 | (5.35) |
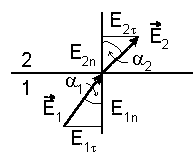 |
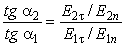 | (5.36) |
Отсюда на основании (5.30) и (5.35) получаем
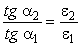 | (5.37) |
Если на среда 1 — проводник, а 2 — диэлектрик, то из соотношения (5.33) следует, что
где n — внешняя к проводнику нормаль. Действительно, т.к. в проводнике E=0, то и P=0. Тогда, так как D = ε 0E + P, то и D1n =0.
Если к заряженному проводнику прилегает однородный диэлектрик, то на границах диэлектрика выступают связанные поверхностные заряды. Найдем их поверхностную плотность σ ‘. Следуя рассуждениям, которые привели к выводу соотношения (4.1), в данном случае получим для нормальной составляющей вектора E
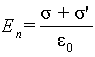 | (5.38) |
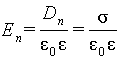 | (5.39) |
С учетом (5.39) из (5.38) получим
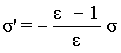 | (5.40) |
Поле внутри однородного изотропного диэлектрика
Если однородный и изотропный диэлектрик полностью заполняет объем, ограниченный эквипотенциальными поверхностями поля сторонних зарядов, то напряженность поля внутри диэлектрика в ε раз меньше, чем напряженность поля сторонних зарядов.
Продемонстрируем справедливость приведенного утверждения на примере плоского конденсатора. П редположим, что пространство между обкладками плоского конденсатора заполнено однородным и изотропным диэлектриком. Тогда на поверхности диэлектрика, прилегающей к пластине с положительным зарядом, появится индуцированный связанный отрицательный заряд, а на противоположной поверхности диэлектрика – индуцированный связанный положительный заряд. Этот связанный заряд σ ‘ является источником электрического поля с напряженностью
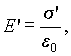 | (5.41) |
причем, согласно ( 5.19), σ ‘ = Pn, где Pn – нормальная составляющая вектора поляризованности.
В результате, в силу принципа суперпозиции поле внутри диэлектрика окажется векторной суммой полей, создаваемых сторонним зарядом, находящимся на обкладках конденсатора, и поверхностным связанным зарядом:
причем векторы E0 и E‘ коллинеарны и направлены навстречу друг другу. Поэтому модуль вектора напряженности будет равен
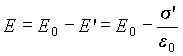 | (5.42) |
Так как диэлектрик предполагается однородным и изотропным, то поляризованность диэлектрика пропорциональна напряженности поля:
Поскольку диэлектрик полностью заполняет объем, ограниченный эквипотенциальными поверхностями поля сторонних зарядов, то вектор E на границе между проводящей обкладкой конденсатора и прилегающим к ней диэлектриком перпендикулярен границе, т.е.
Тогда, с учетом того, что σ ‘ = Pn получается
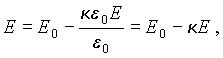 | (5.43) |
откуда для напряженности поля внутри конденсатора имеем
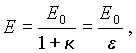 | (5.44) |
где ε — диэлектрическая проницаемость диэлектрика.
🔥 Видео
43. Применение теоремы ГауссаСкачать

Урок 223. Теорема ГауссаСкачать

Лекция 4-5 Доказательство теоремы Гаусса для вектора поляризацииСкачать

Поток вектора напряженности электрического поля. Теорема Гаусса. Практическая часть. 10 класс.Скачать

42. Теорема Гаусса. Расчет электростатических полейСкачать

45. Электрическое смещениеСкачать

Физика. 10 класс. Поток вектора напряженности электрического поля. Теорема Гаусса /18.01.2021/Скачать

Теорема Гаусса - доказательство.Скачать
Электрическое поле. Теорема ГауссаСкачать

Лекция 4-2. Условия на границе раздела двух диэлектриковСкачать

Лекция №2 "Теорема Гаусса, поле проводника, электрический потенциал"Скачать

Билет №16 "Теорема о циркуляции и теорема Гаусса для магнитного поля"Скачать

Как решать задачи с помощью теоремы Гаусса.Скачать

Лекция №4 "Диэлектрики, вектор электрической индукции"Скачать

Лекция по физике №11. Теорема Гаусса. Работа эл. поля. Потенциал. Диполь.Скачать