| Назва | Лекция №2 |
| Дата конвертації | 07.10.2013 |
| Розмір | 49.52 Kb. |
| Тип | Лекция |
mir.zavantag.com > Астрономия > Лекция
Построение перспективы способом архитекторов с одной точкой схода. Рассмотрим пример построения перспективы схематизированного здания (рисунок 2.1). На ортогональных проекциях устанавливаем положение точки зрения и картины. Картину проводим под углом 30º к фасаду через один из углов плана здания. Положение точки зрения S выбираем таким образом, чтобы угол зрения при вершине в точке S составлял 30…35 º, а луч SP был перпендикулярен к картине и не выходил за пределы средней трети угла зрения. На плане определяем положение Fn – точки схода вертикальных прямых плана и их картинные следы 1, 2, 3. Построение перспективы точек плана, можно осуществить как пересечение прямых, имеющих точку схода Fn с лучами, проведенными из точки зрения S в данные точки. Для этого на плане проводим лучи из точки зрения S, и определяем их картинные следы а, б, в, г, д. (рисунок 2.1). Далее приступаем к построению перспективы увеличенной в два раза (рисунок 2.2). Определяем положение точек P и Fn на линии горизонта и картинных следов 1, 2, 3, а, б, в, г, д на основании картины К1, при этом высоту горизонта и все размеры увеличиваем в 2 раза. Картинные следы 1, 2, 3 соединяем с точкой схода Fn. Перспективой лучей, являются вертикальные прямые проведенные из картинных следов а, б, в, г, д. Соединив построенные точки получим перспективу плана здания. Высоты строим таким же образом, как и при двух точках схода, но число построений увеличивается, т.к. приходится определять высоты большего числа ребер объекта. Натуральные величины высот, увеличенные в два раза, откладываем в картинных следах 1, 2, 3. Соединив полученные точки с Fn, и подняв вертикальные ребра с плана, построим перспективу схематизированного здания.
^ Построение перспективы окружности (способ 8-ми точек). Пример 1. Построить перспективу окружности лежащей на предметной плоскости. Радиус окружности R=25 мм, высота горизонта 40 мм (рисунок 2.3).
Опишем вокруг окружности с центром в т. О квадрат ABCD. Точки 1, 2, 3, 4, являются точками касания окружности к сторонам квадрата точки 5, 6, 7, 8 лежат на диагоналях квадрата. Для построения перспективы квадрата (рисунок 2.4), стороны которого не параллельны картине, достаточно использовать точки схода Fл и Fn , картинные следы осей окружности и двух сторон квадрата. Перспективы точек 1, 2, 3, 4,определяем, построив квадрат и оси окружности. Точки на диагоналях найдем, разделив половину стороны квадрата, вынесенную в картину в отношении 0,707. Для чего из точек а и б проведем под углом 45º две прямые и полученным радиусом проведем дугу до пересечения с основанием картины. Из полученных точек проведем прямые в Fn, до пересечения с диагоналями квадрата в точках 5, 6, 7, 8. Соединив, построенные восемь точек получим эллипс. Аналогично выполняется построение окружности в любой, произвольно расположенной плоскости. П На рисунке 2.6 показано построение перспективы вертикальной окружности по восьми точкам. Мы видим, что построение выполнено аналогично примеру 1.
П При построении фронтальной перспективы стороны квадрата перпендикулярные картине имеют точку схода Р. Две другие стороны параллельны картине и картинных следов не имеют. Поэтому, чтобы построить квадрат необходимо построить перспективу диагонали квадрата, которая имеет точку схода D – дистанционную точку (PD=SP). Остальные построения аналогичны предыдущим (рисунок 2.8). ^ Тени в перспективе. При построении теней в перспективе могут быть выбраны следующие положения солнца: а) солнце сбоку слева или справа; б) солнце сзади слева или справа; в) солнце спереди слева или справа. Р а) Солнце сбоку слева (рисунок 2.9). В этом случае лучи параллельны картине и точек схода не имеют. Задаются лучом l и его горизонтальной проекцией l1 . Тени строятся аналогично теням в аксонометрии. б в При факельном освещении задается источник света L и его горизонтальная проекция L1 (рисунок 2.12).
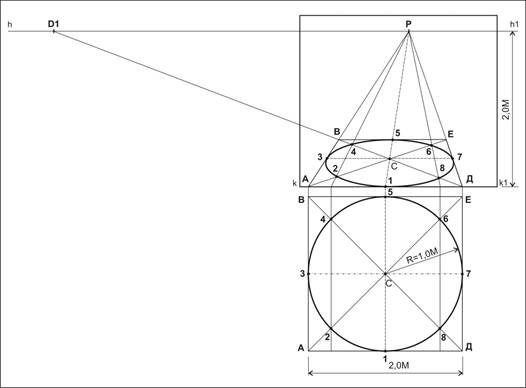
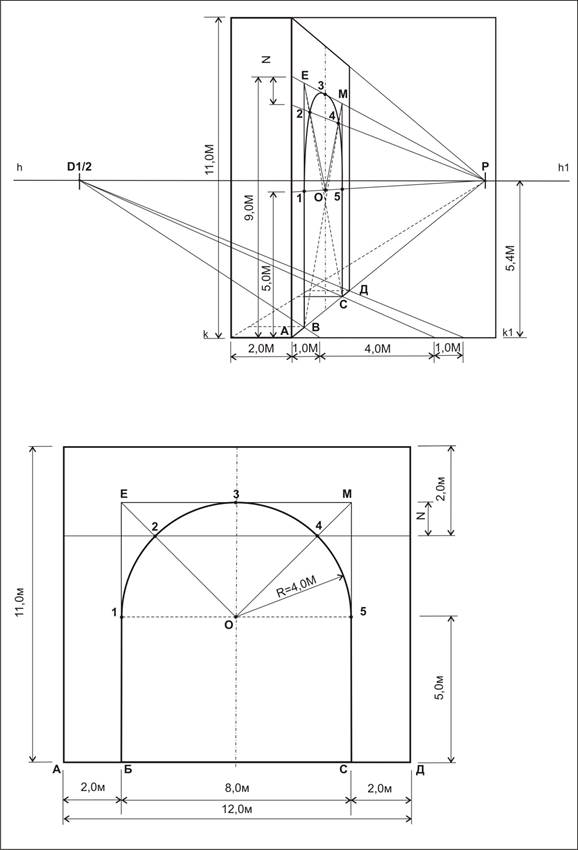
Тени построены при положении солнца сбоку слева (рисунок 2.13). Построение теней аналогично аксонометрии. Определяем контур собственной тени двух объемов ABCD, EFMNO. Сначала строим тени от двух объемов падающих на землю, и определяем общий контур падающей тени. Затем, используя метод лучевых секущих плоскостей, строим тень, падающую от одного объема на другой. Тень от прямой EF идет по сечению. Тень от прямой FM на наклонную плоскость идет в точку пересечения прямой FM с наклонной плоскостью. Содержание Видео:Изображение окружности в перспективе. Эллипс.Скачать  Построение окружности в горизонтальной плоскостиРассмотрим построение перспективы окружности по восьми точкам. Суть способа заключается во вписанной в квадрат ABCD (рис.2.23,а) окружности. Тогда четыре точки касания сторон квадрата (1, 3, 5 и 7) и четыре точки пересечения диагоналей квадрата с окружностью (2, 4, 6 и 8) дают искомые 8 точек для построения перспективы окружности. Точки 1, 3, 5 и 7 имеются при условии, что перспектива квадрата построена. Для нахождения точек 2, 4, 6 и 8 воспользуемся следующей зависимостью. Из соотношения подобных треугольников AOl и 20Е: Из прямоугольного равнобедренного треугольника А19 с углами при вершинах А и 1, равными 45° (рис.2.23,а), величина [1,9]= Чтобы получить точки 2 и 8, необходимо из точек А и 1 провести прямые под углами 45° к прямой AD, получить точку 9, а затем провести окружность радиусом [1,9]. При пересечении с AD эта окружность даст точки 10 и 11. Дальнейшее построение точек 2, 4, 6 и 8 видно из рис.2.23,а. Еще проще доказать, что [2,Е]=[1,9], можно, рассмотрев треугольники 02Е и А19. Они равны, так как они прямоугольные, равны их гипотенузы [0,2]=[А,1], а сами треугольники равнобедренные. Отсюда [2,Е]=[1,9]. Построим перспективу квадрата. Пусть квадрат принадлежит предметной плоскости П], а две его стороны параллельны основанию картины х-х, при этом сторона AD принадлежит (для упрощения) основанию картины (рис.2.23,б). Две другие стороны будут перпендикулярны лг-л;, поэтому они будут иметь точку схода в главной точке Р. Отмечаем на основании картины л;-* точки А’ и D Это — первая сторона квадрата. Проводим А’Р и D’P. Получили направления еще двух сторон квадрата. Включаем в рассмотрение дистанционные точки D 1 и D 2 . Поскольку диагонали квадрата проходят под углом 45° к основанию картины, то их точками схода будут дистанционные точки D 1 и D 2 . Проводим прямые A’D 1 и D’D 2 . Соединив построенные вершины квадрата, получаем его перспективу: A’B’C’D’. На стороне квадрата A’D’ (рис.2.23,б) строим конфигурацию с рис.2.23,а для получения точек 10 и 11. Так как прямые (10,4) и (11,6) имеют точки схода в главной точке картины, проводим (10,Р) и (11,Р). Пересекаясь с перспективами диагоналей квадрата, эти прямые дают искомые 2, 4, 6 и 8 точки. Соединяем плавной кривой точки 1, 2, 3, 4, 5, 6, 7, и 8. В результате должен получиться эллипс (см. рис.2.23,б). Нужно сказать, что центр окружности О не совпадает с центром эллипса. А большой диаметр эллипса не является горизонтальной прямой, если центр окружности не лежит на линии PP]. Если центр окружности находится правее линии РРЬ то большая ось эллипса будет развернута по часовой стрелке (см. рис.2.24) и тем больше, чем дальше центр от линии РРь И наоборот, если центр окружности расположен левее линии РРЬ то ось эллипса будет развернута против часовой стрелки. Для более точного построения эллипса необходимо знать, что в точках 2, 4, 6 и 8 он должен касаться (а не пересекать) прямых, проведенных через эти точки параллельно соответствующим диагоналям квадрата. На рис.2.23 такая прямая (12,8) проведена для точки 8. Точку 12 можно построить, отложив отрезок [11,12]=[11,D] и соединив точку 12 с точкой 8. Прямые (12,8) и (А,С) параллельны (рис.2.23,а), поэтому на перспективе (рис.2.23,б) они сходятся в одной точке — D 1 . На перспективе (рис.2.23,б) находим точку 12 (для этого можно построить окружность с центром в точке 11 радиусом 111,D |), соединяем ее с точкой 8 или с дистанционной точкой D 1 . Этой прямой (12JD 1 ) должен касаться строящийся эллипс. Другие прямые, которых должен касаться эллипс, строятся аналогично. Или точки 2 и 6 соединяются с дистанционной точкой D 2 , а точки 4 и 8 — с D 1 , или строятся соответствующие окружности, наподобие той, что была построена для определения точки 12. Построим две окружности в перспективе, одна из которых расположена прямо перед наблюдателем так, что ее центр находится на линии PP], а другая — правее, но так же, как и первая, касается основания картины. Обе перспективы построены по восьми точкам. Видно, что если первая окружность имеет вид эллипса, у которой большой диаметр параллелен основанию картины, то большой диаметр второго эллипса имеет острый угол с основанием картины. Искажение второго эллипса объясняется недопустимо большим углом зрения, под которым она построена. Поэтому, если нельзя уменьшить угол зрения, надо изображение скорректировать, изобразив вторую окружность как и первую (на рис.2.23 скорректированная перспектива второй окружности изображена штриховой линией). Видео:Перспектива. Метод архитекторовСкачать 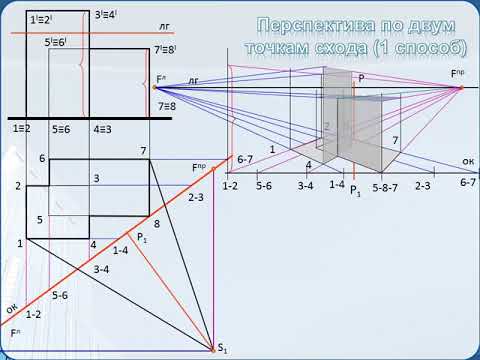 Построение окружности в профильной плоскостиВ вертикальной плоскости окружность по восьми точкам строится аналогично (рис.2.24). Сначала строим перспективу квадрата в горизонтальной плоскости, а затем в профильной. При этом [А’,Е’]= [A’,D’]. Найдя центр горизонтальной окружности О и точку 2, строим профильные проекции восьми точек, как показано на рис.2.24. Видео:Построение окружности по трём точкам.Скачать  Построение окружности во фронтальной плоскостиОкружность во фронтальной плоскости (плоскости, параллельной картине) имеет перспективу в виде окружности. Если окружность находится в картинной плоскости, то ее перспективное изображение совпадает с самой окружностью, и диаметр перспективы окружности равен диаметру самой окружности. По мере удаления от наблюдателя диаметр перспективы окружности уменьшается. На рис.2.25 показаны четыре окружности, плоскости которых параллельны картине, а центры находятся на прямой, перпендикулярной картине. Перспектива этой прямой — [0′,Р]. Первая окружность с центром в точке О расположена в картинной плоскости. Остальные окружности равны ей по диаметру. Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать  Построение перспективы полуциркульной арки с одной точкой схода.Тема 5. Построение окружности в перспективе. Построение перспективы окружности по 8 точкам. При помощи циркуля чертим окружность радиусом 1 м с центром в точке С. Через центр окружности проводим вертикальную и горизонтальную оси симметрии. При их пересечении с окружностью получаем 4 точки. Перспективу окружности удобнее строить при помощи вспомогательного квадрата. Вписываем нашу окружность в квадрат со сторонами 2Х2 м. Обозначим его вершины А, В, Е, Д,начиная с левого нижнего угла, двигаясь по часовой стрелке. Проведём в нём две диагонали. Диагонали при пересечении с окружностью дадут ещё 4 точки. В результате мы получили 8 точек. Обозначим их 1,2,3,4,5,6,7,8, начиная с нижней точки по часовой стрелке. Приступаем к построению перспективы окружности. Задаём высоту горизонта, строим картинную плоскость, проводим линию горизонта и на ней отмечаем центральную точку схода Р. Находим дистанционные точки D1 и D2. На основании картинной плоскости отмечаем в заданном масштабе отрезок А Д. Из этих точек проводим прямые в точку Р. Затем из точки Д проводим прямую в дистанционную точку D1. При пересечении с прямой АР она отметит нам глубину квадрата в перспективном сокращении. Достраиваем перспективу квадрата. Из его вершин проведём две диагонали и получим точку С. Через неё проведём оси симметрии. Одна будет направлена параллельно основанию картины, а другая будет направлена в точку Р. При пересечении их со сторонами квадрата получим 4 точки 1,3,5,7. Для нахождения оставшихся 4 точек на плане окружности проведём вертикальные прямые через точки 2,4 и 6,8. Измерим расстояния до этих прямых от точки О и перенесём его на основание картинной плоскости. Из этих точек проведём прямые в точку Р, в местах их пересечения с диагоналями квадрата будут располагаться остальные 4 точки 2,4,6,8. По полученным в перспективе точкам строим нашу окружность.
Построение перспективы окружности расположенной в предметной плоскости по 8 точкам. Таким же способам можно строить окружность на вертикальных плоскостях. Если окружность находится на заданном расстоянии от картинной плоскости, то при построении квадрата надо от точки А сначала отложить это расстояние, а потом отложить сторону квадрата. Построение перспективы полуциркульной арки с одной точкой схода. Построим отдельно стоящую прямоугольную арку, которая имеет сквозной полуциркульный проём. Ширина проёма 8м, высота 9м. Высота всего сооружения 11м. Проём находится на расстоянии 2 м от левого и правого углов объекта и завершается полуциркульной аркой с радиусом 4м. Сначала начертим сам проём, вписав его в прямоугольник шириной 8м и высотой 11м. Обозначим вершины этого прямоугольника, начиная с левой нижней грани А, Б, С, Д, по часовой стрелке. Проводим вертикальную ось симметрии. На ней отмечаем точку О (центр окружности) на высоте 5м. При помощи циркуля строим полуарку (радиус 4м). Через точку О проводим горизонтальную прямую. Она, пересекаясь с вертикальными сторонами прямоугольника, отмечает 2 точки начала полуокружности, а вертикальная ось симметрии, пересекая полуокружность, даёт 3 точку. Из центра О проводим две прямые в точки Би С. Они, пересекая нашу полуокружность, дают ещё 2 точки. Теперь мы можем построить полуокружность в перспективе по 5 точкам 1,2,3,4,5. Отметим их на чертеже, начиная с левого нижнего начала полуокружности, двигаясь по часовой стрелке. Начинаем строить наш проём в перспективе. Задаём высоту линии горизонта (5,4м). Строим картинную плоскость, проводим линию горизонта, отмечаем на ней центральную точку схода Р. Её лучше сместить вправо от центра. Находим дистанционные точки D1 и D2, но так как они могут располагаться за плоскостью листа, то для построения будем использовать дробные дистанционные точки D1/2 и D2/2. На основании картинной плоскости отмечаем точку А- точку начала стены и из неё проводим вверх вертикальную границу стены, равной 11 м. Из верхней и нижней точек проводим прямые в точку Р. От нижней точки стены на основании картинной плоскости откладываем половину длинны до арки 1,0м (мы используем дробные дистанционные точки).
Построение перспективы полуциркульной арки с одной точкой схода. Конец отрезка соединяем с дробной дистанционной точкой D1/2 и на основании стены получаем начало нашего проёма В. Затем, на основании картинной плоскости к первому отрезку прибавляем половину ширины нашего проёма 4м. Соединяем конец этого отрезка с точкой D1/2 и эта прямая, пересекая основание стены, отметит точку С. Отрезок ВС — это ширина нашего проёма в перспективе. После этого, на основании картинной плоскости, к 4 м прибавляем отрезок 1м и конец этого отрезка соединяем с точкой D1/2 . Таким образом, мы получили крайнюю точку Д. Из точек В и С проводим вертикальные границы нашего проёма. На вертикальной грани начала стены отмеряем высоту проёма 9,0м и проводим прямую переноса в точку Р. Эта прямая, пересекая вертикали, проведенные из точек В и С, отмечает высоту проёма. Начертив проём в перспективе, проводим в нём две диагонали и на их пересечении получаем ось симметрии. Поднимаем её наверх до верхней границы проёма. На ней она отмечает точку 3′. Теперь на грани стены отмеряем высоту точки О (5,0м). Из неё проводим прямую переноса в точку Р и на оси симметрии получаем точку О. На крайних границах проёма она отмечает точки 1′ и5′. Для того чтобы построить в перспективе точки 2 и 4, надо на чертеже проёма провести через них горизонтальную прямую и измерить расстояние N от этой прямой до отрезка Е М. Переходим к перспективному изображению. Отмеряем расстояниеN на грани стены и соединяем полученную точку с точкой Р. Из точки О проводим два отрезка в точки Е и М. Эти отрезки, пересекаясь с прямой идущей в точку Р,дадут нам точки 2 и 4. Используя точки 1, 2, 3, 4, 5, строим полуокружность в перспективе. Из точки С проводим влево прямую до вертикали ВЕ. Она отмечает толщину стены. 🌟 ВидеоПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать  Построение эллипса по восьми точкам в прямоугольной диметрииСкачать 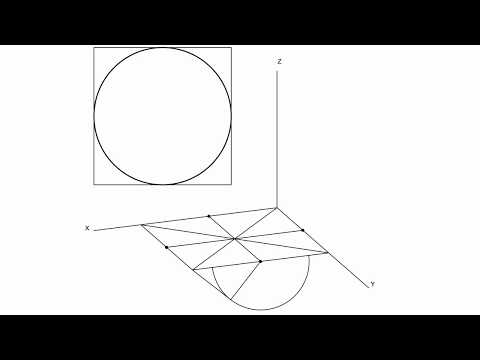 Как начертить овал. Эллипс вписанный в ромбСкачать  Определение центра дуги окружности, построение окружности по 3 точкамСкачать  Построение эллипса по 5 точкам в AutoCADСкачать 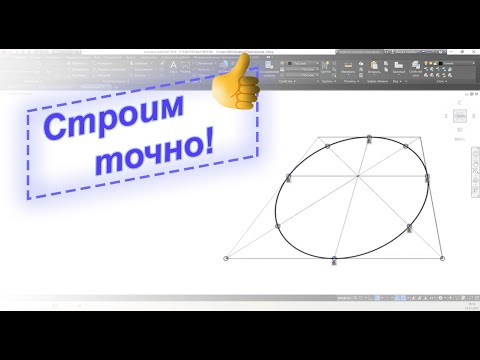 Окружность. 7 класс.Скачать  Перспектива. Построение окружности в перспективе.Скачать  Круг в перспективеСкачать 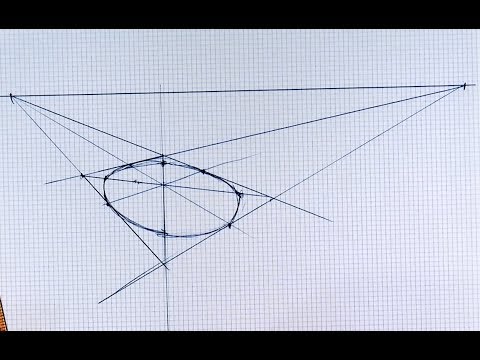 Построение окружности в диметрииСкачать  Как начертить овал в горизонтальной плоскостиСкачать  Уравнение окружности (1)Скачать  КАК РИСОВАТЬ ЭЛЛИПСЫ. Простой и быстрый способ рисования ЭЛЛИПСОВСкачать  Построение 8 угольника циркулемСкачать  1 2 4 сопряжение окружностейСкачать  4K Построение эллипса по точкам, ellipse constructionСкачать  Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  |
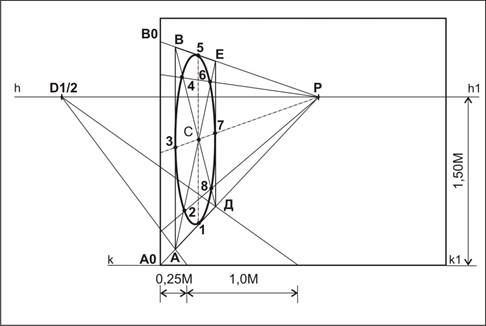
ример 2. Дана горизонтальная проекция вертикальной окружности R=25 мм. Построить перспективу окружности при высоте горизонта 30 мм (рисунок 2.5).
ример 3. Построить фронтальную перспективу окружности, лежащей на горизонтальной плоскости. R=25 мм, высота горизонта 40 мм (рисунок 2.7).
ассмотрим каждый из случаев.
) ^ Солнце сзади слева (рисунок 2.10). В этом случае солнце находится за зрителем слева. Поэтому точка схода горизонтальных проекций лучей будет находиться справа на линии горизонта L1 , а точка схода лучей L ниже горизонта на одной вертикали с L1 , выбирается произвольно.
) ^ Солнце спереди справа (рисунок 2.11). В этом случае солнце находится перед зрителем справа. Точки схода лучей L находятся справа выше горизонта на одной вертикальной линии с L1 – точкой схода горизонтальных проекций лучей.
