Отрезки соединяющие вершины треугольника с точками касания вписанной окружности

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

We are checking your browser. mathvox.ru

Видео:ЕГЭ Математика Задание 6#27935Скачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d9265dd8b242de5 • Your IP : 85.95.188.35 • Performance & security by Cloudflare

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

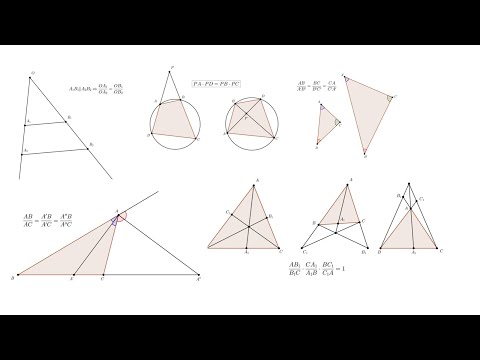
Точка Жергонна треугольника.

Теорема.

Три чевианы, соединяющие вершины треугольника с точками пересечения вписанной окружности и сторон треугольника, пересекаются в одной точке.

Доказательство.

Пусть D, E, F — точки пересечения вписанной окружности и сторон треугольника BC, AC и AB соответственно.

AF=AE, BF=BD, CD=CE (свойство отрезков касательных, проведенных из одной точки, к окружности).

По теореме Чевы отрезки AD, BE и СF пересекаются в одной точке.

Точка Жергонна — точка пересечения чевиан треугольника, соединяющих вершины треугольника с точками пересечения вписанной окружности и сторон треугольника.

Теорема Жергонна.

Пусть G — точка Жергонна треугольника ABC и D, E, F — точки пересечения вписанной окружности и сторон треугольника BC, AC и AB соответственно. Тогда выполняются следующие равенства:

Видео:Задача №255 [НЕДЕТСКАЯ ГЕОМЕТРИЯ #1]Скачать

Математика, которая мне нравится

Математика для школьников и студентов, обучение и образование

Видео:Калитки. Лайфхак для вписанных и вневписанных окружностейСкачать

Точка Жергонна, теорема Жергонна

Жозеф Диас Жергонн (Joseph Diaz Gergonne, 19.06.1771 – 4.05.1859) — французский математик, геометр, на которого оказал большое влияние Монж, с 1830 по 1844 год был ректором университета Монпелье.

В 1810 году Жергонн начал издавать свой журнал, который имел официальное название Annales de mathématiques pures et appliquées, но стал известен как Annales de Gergonne. Этот журнал издавался в течение 22 лет, в основном в нем печатались работы, посвященные геометрии как основной области интересов Жергонна. В нем печатались работы многих известных математиков: Понселе, Плюкера, Брианшона, Галуа и др.

Жергонн дал элегантное решение задачи Аполлония: построить окружность, которая касается трех данных окружностей. Он ввел термин “поляра” и принцип двойственности в проективную геометрию.

Вот так Жергонн говорил о математических теориях:

“Невозможно чувствовать удовлетворение от того, что в некоторой теории сказано все, пока она не может быть объяснена в нескольких словах любому прохожему, с которым вы встретитесь на улице.’’

Красиво, не правда ли? Жаль, что это невозможно…

Определение. Точкой Жергонна называется точка пересечения отрезков, которые соединяют вершины треугольника с точками касания сторон, противоположных этим вершинам, и вписанной в треугольник окружности.

Пусть точка — центр вписанной окружности треугольника . Пусть вписанная окружность касается сторон треугольника и в точках и соответственно. Точка Жергонна — это точка пересечения отрезков и .

Докажем, что эти три отрезка действительно пересекаются в одной точке. Заметим, что центр вписанной окружности — это точка пересечения биссектрис углов треугольника , а радиусы вписанной окружности и перпендикулярны сторонам треугольника. Тем самым, имеем три пары равных треугольников ( и , и , и ).

Произведения и равны, поскольку

следовательно, отношение этих произведений равно , и по теореме Чевы, отрезки пересекаются в одной точке.

Замечание. Отрезок, соединяющий вершину треугольника с точкой, лежащей на противоположной стороне или ее продолжении, называется чевианой.

Теорема Жергонна. Пусть три чевианы и пересекаются в точке внутри треугольника . Тогда выполняются следующие равенства:

1)

2)

Доказательство. Поскольку выполняются очевидные равенства

то равенства 1) и 2) эквивалентны. Докажем первое из них.

Рассмотрим отношения площадей треугольников

Здесь мы используем тот факт, что отношения площадей треугольников, имеющих общую сторону, равны отношениям их высот. Соответственно, отношение высот будет равно отношению длин параллельных отрезков, проведенных к общей стороне из противоположной вершины.

🔥 Видео

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

#2str. Счет отрезковСкачать

РОСС ГЕЛЛЕР + ДЖО ТРИББИАНИ | вычисляют площадь треугольника по точкам касания вписанной окружностиСкачать

Вписанная окружность 1Скачать

[7] Окружности с нуля для ЕГЭ по математике. Внешнее касание окружностей. Конструкция из демоверсии.Скачать

Геометрия Точка касания вписанной окружности делит гипотенузу прямоугольного треугольника на отрезкиСкачать

Отрезки касательных. Применение Чевы и Ван-Обеля. Точка Жергонна. (Геометрические конструкции)Скачать

Почему геометрия — это красиво?Скачать

Построить описанную окружность (Задача 1)Скачать

№1,17 | Все теория по планиметрии за 4 часа | Решаем все прототипы №1 из ФИПИСкачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

✓ Как вневписанная окружность Герону помогла | Ботай со мной #083 | Борис ТрушинСкачать

Задачи по геометрии треугольникаСкачать

ЕГЭ 2021 Математика. Метод площадей. Теорема Чевы. Вневписанная окружностьСкачать