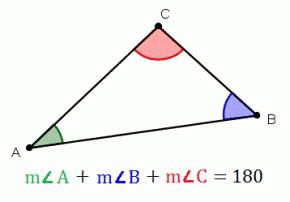
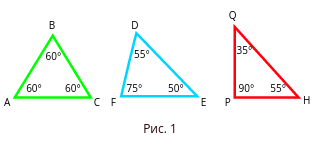Треугольник всегда 180 градусов (3 видео)

Сумма углов треугольника

Сумма углов треугольника — это сумма
всех внутренних углов треугольника.

Так, как углы измеряются в градусах, соответственно значение
суммы углов треугольника также измеряется в градусах.

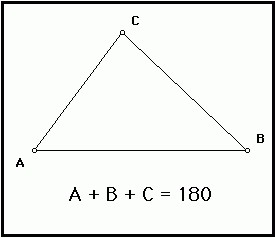
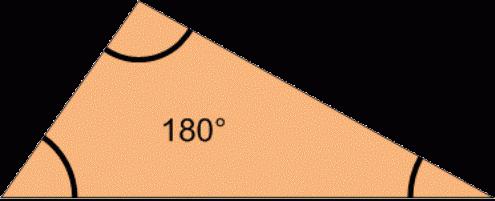
Сумма углов треугольника есть величина постоянная,
неизменяемая, она равна 180 градусам, вне зависимости
от вида рассматриваемого треугольника.

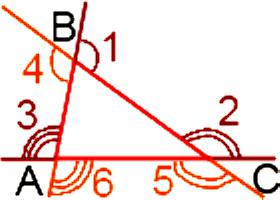
На рисунке 1 изображены равносторонний,
разносторонний и прямоугольный треугольники,
их суммы внутренних углов равны 180 градусам.

Также, существует теорема, которая доказывает
утверждение о том, что сумма углов треугольника
180 градусов, она называется теоремой
о сумме углов треугольника.

Теорема о сумме углов треугольника — это теорема в
геометрии о сумме углов произвольного треугольника на плоскости.

Содержание

Сумма углов треугольника
Сумма углов треугольника. Теорема о сумме углов треугольника
Виды по величине углов
Свойства
Теорема о сумме углов треугольника
Следствие
Свойство внешних углов
Прямоугольный треугольник
Сумма углов равнобедренного треугольника
Равносторонний треугольник
Тупоугольный треугольник
💡 Видео

Видео:Почему сумма углов в треугольнике 180 градусов? #умскул #егэпрофиль #математикаегэ #математикаСкачать

Сумма углов треугольника

Сумма треугольника равна 180 градусов.

Это легко доказать. Нарисуйте треугольник. Через одну из его вершин проведите прямую, параллельную противоположной стороне, и найдите на рисунке равные углы. Сравните с решением в конце статьи.

А мы разберем задачи ЕГЭ, в которых фигурирует сумма углов треугольника.

1. Один из внешних углов треугольника равен 85 градусов. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.

Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Следовательно, сумма двух других углов треугольника равна 85 градусов, а их отношение равно 2:3. Пусть эти углы равны 2х и 3х. Получим уравнение

2. Один из углов равнобедренного треугольника равен 98 градусов. Найдите один из других его углов. Ответ дайте в градусах.

Как вы думаете, может ли равнобедренный треугольник иметь два угла по 98 градусов?

Нет, конечно! Ведь сумма углов треугольника равна 180 градусов. Значит, один из углов треугольника равен , а два других равны .

3. На рисунке угол равен , угол равен , угол равен . Найдите угол . Ответ дайте в градусах.

Давайте отметим на чертеже еще несколько углов. Они нам понадобятся.

Сначала найдем угол .

Угол , смежный с углом равен .

Заметим, что такой способ решения — не единственный. Просто находите и отмечайте на чертеже все углы, которые можно найти.

Ты нашел то, что искал? Поделись с друзьями!

4. Углы треугольника относятся как . Найдите меньший из них. Ответ дайте в градусах.

Пусть углы треугольника равны , и . Запишем, чему равна сумма углов этого треугольника.

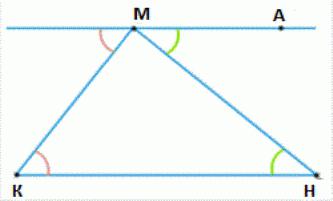
Как же все-таки доказать, что сумма углов треугольника равна 180 градусов? Очень просто. На нашем рисунке угол равен углу (они накрест лежащие). Угол равен углу (тоже накрест лежащие). Развернутый угол равен . Значит, и сумма углов треугольника тоже равна 180 градусов.

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Сумма углов треугольника. Теорема о сумме углов треугольника

Треугольник представляет собой многоугольник, имеющий три стороны (три угла). Чаще всего стороны обозначают маленькими буквами, соответствующими заглавным буквам, которыми обозначают противоположные вершины. В данной статье мы ознакомимся с видами этих геометрических фигур, теоремой, которая определяет, чему равняется сумма углов треугольника.

Видео:Почему сумма углов треугольника 180 градусов?Скачать

Виды по величине углов

Различают следующие виды многоугольника с тремя вершинами:

остроугольный, у которого все углы острые;
прямоугольный, имеющий один прямой угол, при этом стороны, его образующие, называют катетами, а сторона, которая размещена противоположно прямому углу, именуется гипотенузой;
тупоугольный, когда один угол тупой;
равнобедренный, у которого две стороны равные, и называются они боковыми, а третья – основанием треугольника;
равносторонний, имеющий все три равные стороны.

Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Свойства

Выделяют основные свойства, которые характерны для каждого вида треугольника:

напротив большей стороны всегда располагается больший угол, и наоборот;
напротив равных по величине сторон находятся равные углы, и наоборот;
у любого треугольника есть два острых угла;
внешний угол больше по сравнению с любым внутренним углом, не смежным с ним;
сумма каких-либо двух углов всегда меньше 180 градусов;
внешний угол равняется сумме остальных двух углов, которые не межуют с ним.

Видео:ПОЧЕМУ СУММА УГЛОВ В ТРЕУГОЛЬНИКЕ РАВНА 180? #shorts #геометрия #егэ #огэ #треугольникСкачать

Теорема о сумме углов треугольника

Теорема утверждает, что если сложить все углы данной геометрической фигуры, которая расположена на евклидовой плоскости, то их сумма будет составлять 180 градусов. Попробуем доказать данную теорему.

Пускай у нас есть произвольный треугольник с вершинами КМН.

Видео:Сумма углов треугольника не всегда равна 180º #vertdider #veritasiumСкачать

Следствие

Из выше доказанной теоремы вытекает следующее следствие: любой треугольник имеет два острых угла. Чтобы это доказать, допустим, что данная геометрическая фигура имеет всего один острый угол. Также можно предположить, что ни один из углов не является острым. В этом случае должно быть как минимум два угла, величина которых равна или больше 90 градусов. Но тогда сумма углов будет больше, чем 180 градусов. А такого быть не может, поскольку согласно теореме сумма углов треугольника равна 180° — не больше и не меньше. Вот это и нужно было доказать.

Видео:Сумма углов 180 градусовСкачать

Свойство внешних углов

Чему равна сумма углов треугольника, которые являются внешними? Ответ на этот вопрос можно получить, применив один из двух способов. Первый заключается в том, что необходимо найти сумму углов, которые взяты по одному при каждой вершине, то есть трех углов. Второй подразумевает, что нужно найти сумму всех шести углов при вершинах. Для начала разберемся с первым вариантом. Итак, треугольник содержит шесть внешних углов – при каждой вершине по два.

Кроме этого, известно, что внешний угол у треугольника равняется сумме двух внутренних, которые не межуются с ним. Следовательно,

∟1 = ∟А + ∟С, ∟2 = ∟А + ∟В, ∟3 = ∟В + ∟С.

Из этого получается, что сумма внешних углов, которые взяты по одному возле каждой вершины, будет равна:

∟1 + ∟2 + ∟3 = ∟А + ∟С + ∟А + ∟В + ∟В + ∟С = 2 х (∟А + ∟В + ∟С).

С учетом того, что сумма углов равняется 180 градусам, можно утверждать, что ∟А + ∟В + ∟С = 180°. А это значит, что ∟1 + ∟2 + ∟3 = 2 х 180° = 360°. Если же применяется второй вариант, то сумма шести углов будет, соответственно, большей в два раза. То есть сумма внешних углов треугольника будет составлять:

∟1 + ∟2 + ∟3 + ∟4 + ∟5 + ∟6 = 2 х (∟1 + ∟2 + ∟2) = 720°.

Видео:Почему сумма углов треугольника 180 градусов? 📚 #егэ #профильнаяматематика #профиль #егэпрофильСкачать

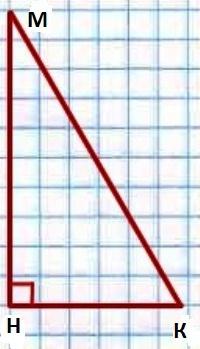
Прямоугольный треугольник

Чему равняется сумма углов прямоугольного треугольника, являющихся острыми? Ответ на этот вопрос, опять же, вытекает из теоремы, которая утверждает, что углы в треугольнике в сумме составляют 180 градусов. А звучит наше утверждение (свойство) так: в прямоугольном треугольнике острые углы в сумме дают 90 градусов. Докажем его правдивость.

Итак, согласно теореме о сумме углов ∟К + ∟М + ∟Н = 180°. В нашем условии сказано, что ∟Н = 90°. Вот и получается, ∟К + ∟М + 90° = 180°. То есть ∟К + ∟М = 180° — 90° = 90°. Именно это нам и следовало доказать.

В дополнение к вышеописанным свойствам прямоугольного треугольника, можно добавить и такие:

углы, которые лежат против катетов, являются острыми;
гипотенуза треугольна больше любого из катетов;
сумма катетов больше гипотенузы;
катет треугольника, который лежит напротив угла 30 градусов, в два раза меньше гипотенузы, то есть равняется ее половине.

Как еще одно свойство данной геометрической фигуры можно выделить теорему Пифагора. Она утверждает, что в треугольнике с углом 90 градусов (прямоугольном) сумма квадратов катетов равняется квадрату гипотенузы.

Видео:Геометрия 7 класс (Урок№23 - Сумма углов треугольника.)Скачать

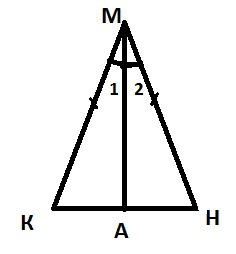
Сумма углов равнобедренного треугольника

Ранее мы говорили, что равнобедренным называют многоугольник с тремя вершинами, содержащий две равные стороны. Известно такое свойство данной геометрической фигуры: углы при его основании равны. Докажем это.

Возьмем треугольник КМН, который является равнобедренным, КН – его основание.

Но нас интересует, какова сумма углов треугольника (равнобедренного). Поскольку в этом отношении у него нет своих особенностей, будем отталкиваться от теоремы, рассмотренной ранее. То есть мы можем утверждать, что ∟К + ∟М + ∟Н = 180°, или 2 х ∟К + ∟М = 180° (поскольку ∟К = ∟Н). Данное свойство доказывать не будем, поскольку сама теорема о сумме углов треугольника была доказана ранее.

Кроме рассмотренных свойств об углах треугольника, имеют место и такие немаловажные утверждения:

в равнобедренном треугольнике высота, которая была опущена на основание, является одновременно медианой, биссектрисой угла, который находится между равными сторонами, а также осью симметрии его основания;
медианы (биссектрисы, высоты), которые проведены к боковым сторонам такой геометрической фигуры, равны.

Видео:Сумма углов треугольникаСкачать

Равносторонний треугольник

Его еще называют правильным, это тот треугольник, у которого равны все стороны. А поэтому равны также и углы. Каждый из них составляет 60 градусов. Докажем это свойство.

Допустим, что у нас есть треугольник КМН. Нам известно, что КМ = НМ = КН. А это значит, что согласно свойству углов, расположенных при основании в равнобедренном треугольнике, ∟К = ∟М = ∟Н. Поскольку согласно теореме сумма углов треугольника ∟К + ∟М + ∟Н = 180°, то 3 х ∟К = 180° или ∟К = 60°, ∟М = 60°, ∟Н = 60°. Таким образом, утверждение доказано.

Существуют еще такие свойства, характерные для равностороннего треугольника:

медиана, биссектриса, высота в такой геометрической фигуре совпадают, а их длина вычисляется как (а х √3) : 2;
если описать вокруг данного многоугольника окружность, то ее радиус будет равен (а х √3) : 3;
если вписать в равносторонний треугольник окружность, то ее радиус будет составлять (а х √3) : 6;
площадь этой геометрической фигуры вычисляется по формуле: (а2 х √3) : 4.

Видео:Едим Еду на Каждую Букву АЛФАВИТА !Скачать

Тупоугольный треугольник

Согласно определению тупоугольного треугольника, один из его углов находится в промежутке от 90 до 180 градусов. Но учитывая то, что два остальных угла данной геометрической фигуры острые, можно сделать вывод, что они не превышают 90 градусов. Следовательно, теорема о сумме углов треугольника работает при расчете суммы углов в тупоугольном треугольнике. Получается, мы смело можем утверждать, опираясь на вышеупомянутую теорему, что сумма углов тупоугольного треугольника равна 180 градусам. Опять-таки, данная теорема не нуждается в повторном доказательстве.