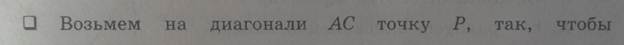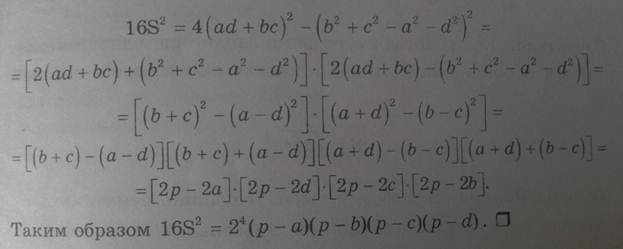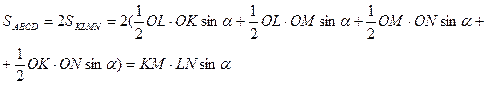Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Различают выпуклые и невыпуклые и звездчатые четырёхугольники. Выпуклым четырехугольником называется четырехугольник, у которого все углы меньше развернутого угла. Четырехугольник, у которого угол больше развернутого называется невыпуклым
Виды четырёхугольников
Параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны;
Прямоугольник — четырёхугольник, у которого все углы прямые;
Ромб — четырёхугольник, у которого все стороны равны;
Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны;
Трапеция — четырёхугольник, у которого две противоположные стороны параллельны;
(Дельтоид — четырёхугольник, у которого две пары смежных сторон равны.)
- Сумма углов четырёхугольника равна 2 π = 360°.
- Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов равна 180° (). См. также теорема Птолемея.
- Четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны ()
- Формула Эйлера: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумму квадратов его диагоналей.
- Средние линии четырёхугольника и отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся ею пополам.
- Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершин.
- Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
- Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
- Средние линии четырёхугольника равны тогда и только тогда, когда равны суммы квадратов его противоположных сторон.
Теорема Вариньона
Четырёхугольник, вершины которого совпадают с серединами сторон произвольного четырёхугольника, является параллелограммом, стороны которого параллельны диагоналям исходного четырёхугольника.
или сокращённо
Середины сторон произвольного четырёхугольника — вершины параллелограмма
Доказательство
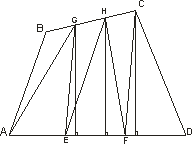
Проведём диагональ AC. Отрезки EF и GH будут средними линиями треугольников 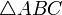
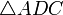
Доказательство, что площадь параллелограмма равна половине площади исходного четырехугольника: Пусть диагональ 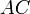
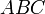
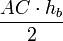
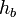
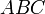
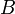
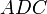
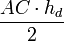
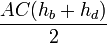
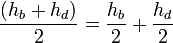
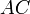
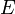
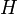
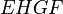
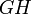
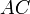
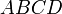
Теорема Эйлера
в любом четырехугольнике сумма квадратов сторон равна сумме квадратов диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналями
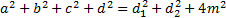

Следствие: Сумма квадратов длин равна диагоналей параллелограмма равна сумме квадратов длин его сторон
Теорема Птолемея
Для любого выпуклого четырёхугольника ABCD вписанного в окружность, сумма произведений длин противоположных сторон равна произведению длин диагоналей AB*DC+BC*AD=BD*AC
Теорема Брахмагупты(площадь вписанного в окружность четырёхугольника)
Если a, b, c, d – длины сторон четырёхугольника, 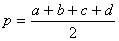
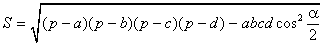
В качестве α здесь можно взять сумму любой из двух пар противоположных углов, результат от этого не зависит. В случае четырёхугольника, вписанного в окружность, эта формула принимает более простой вид: 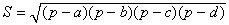
это равенство и называется формулой Брахмагупты. Если четырёхугольник имеет и описанную и вписанную окружности, то формула становится совсем короткой: 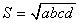
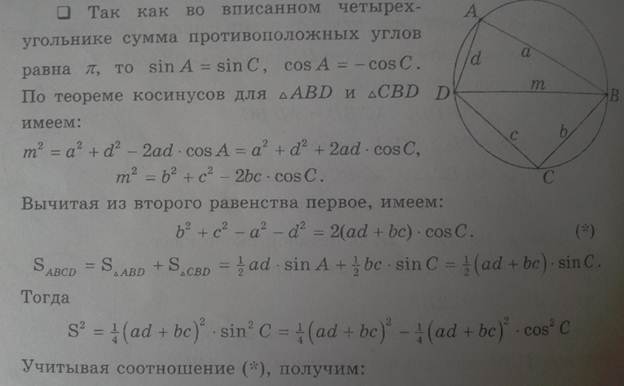
Видео:Малая теорема Ферма и теорема Эйлера | Ботай со мной #037 | Борис Трушин !Скачать

Бимедианы четырехугольника
проект по геометрии (9 класс) на тему
Тема работы посвящена бимедианам четырехугольника и теореме Вариньона. Эти замечательные понятия не входят в программу по геометрии для средней школы. Однако при решении целого класса задач эти понятия позволяют легко получить решение, в то время когда традиционные подходы приводят к громоздким и утомительным преобразованиям
Видео:Теорема Эйлера для четырехугольника | Дополнительные главы школьной геометрииСкачать

Скачать:
| Вложение | Размер |
|---|---|
| teorema_varinona.pptx | 240.84 КБ |
| teorema_varinona.doc | 603 КБ |
Бесплатный марафон подготовки к ЕГЭ на зимних каникулах
Учи.Дома запускает бесплатный марафон в котором каждый день. В течении 5 дней утром ты будешь получать одно задание по выбранному предмету, а вечером его решение. Твоя задача, успеть выполнение задание до того как получишь ответ.
Бесплатно, онлайн, подготовка к ЕГЭ
Предварительный просмотр:
Видео:Остаток от деления 14^245 на 90 | Теорема Эйлера | Теория чисел | КАК РЕШАТЬ?Скачать

Подписи к слайдам:
Бимедианы четырехугольника Автор работы Харитонов Илья, ученик 9-Б класса Место выполнения работы: г.Ставрополь МБОУ СОШ №32 Научный руководитель: Кривокора А.С., учитель математики и физики
Актуальность темы 1. Данная тема является дополнением и углублением изученных в курсе геометрии свойств. 2. Применение опыта решения планиметрических задач с использованием теоремы Вариньона и следствий из нее помогает повысить уровень пространственного воображения и уровень логической культуры. 3. Изучение данной темы поможет более глубоко подготовиться к вступительным экзаменам и успешному участию в математических конкурсах и олимпиадах. 4. Данная работа может быть использована для проведения практических занятий на элективных курсах с учащимися выпускных классов и при подготовке к Единому Государственному Экзамену и поступлению в ВУЗ.
Цель исследования Изучить теорию вопроса и исследовать приемы решений планиметрических задач с использованием теоремы Вариньона и следствий из нее.
Объект и предмет исследования Объект исследования – Теорема Вариньона Предметом данного исследования являются следствие из теоремы необходимые для решение задач.
« Обладая литературой более обширной, чем алгебра и арифметика вместе взятые, и, по крайней мере, столь же обширной, как анализ, геометрия в большей степени чем любой другой раздел математики, является богатейшей сокровищницей интереснейших, но полузабытых вещей, которыми спешащее поколение не имеет времени насладиться». Е. Т. Белл.
1. Основные теоретические сведения.
Определение Бимедианы четырехугольника -это отрезки, соединяющие середины противоположных сторон.
Одна из основных теорем о бимедианах четырехугольника принадлежит французскому механику и инженеру Пьеру Вариньону (1654 – 1722), написавшему учебник по элементарной геометрии (издан в 1731 г.), в котором эта теорема впервые и появилась.
Теорема Вариньона . Формулировка: Четырехугольник, образованный путем последовательного соединения середин сторон выпуклого четырехугольника, является параллелограммом, и его площадь равна половине площади данного четырехугольника
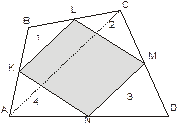
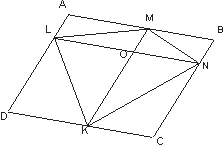
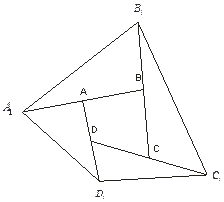
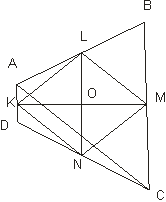
Доказательство: 1. рассмотрим (рис. ) одну из сторон четырехугольника KLMN , например KL . Так как KL является средней линией треугольника ABC , то KL ║ AC . По тем причинам MN ║ AC . Следовательно, KL ║ NM и KL = MN = AC /2 . таким образом, KLMN — параллелограмм. Этот параллелограмм называется параллелограммом Вариньона данного четырехугольника.
Доказательство: 2 . средняя линия треугольника отсекает от него треугольник, площадь которого в четыре раза меньше площади исходного треугольника. Поэтому сама сумма площадей первого и третьего треугольников (см. рис.) равна четверти площади всего четырехугольника. То же и относительно суммы площадей второго и четвертого треугольников. Поэтому площадь параллелограмма KLMN составляет половину площади четырехугольника ABCD Теорема доказана.
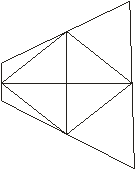
Следствия из теоремы. 1. Следствие 1. Параллелограмм Вариньона является ромбом тогда и только тогда, когда в исходном четырехугольнике: а) диагонали равны (рис. а); б) бимедианы перпендикулярны (рис.б). Рис. а) Рис. б)
2. Параллелограмм Вариньона является прямоугольником тогда и только тогда, когда в исходном четырехугольнике: а) диагонали перпендикулярны(рис. а); б) бимедианы равны (рис.б). Рис. а) Рис. б)
Следствие 2 Бимедианы четырехугольника и отрезок, соединяющий середины диагоналей, пересекаются в одной точке и делятся этой точкой пополам.
Следствие 3.(теорема Эйлера). Для четырехугольника сумма квадратов всех сторон равна сумме квадратов диагоналей плюс учетверенный квадрат отрезка, соединяющего середины диагоналей, то есть .
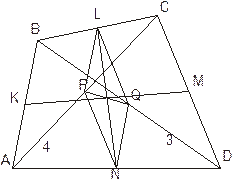
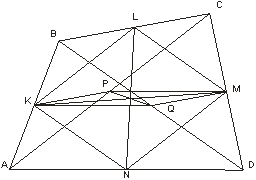
.Следствие 4.(теорема о бабочках). Суммы площадей накрест лежащих четырехугольников, образованных пересечением бимедиан LN и KM выпуклого четырехугольника ABCD равны (рис. ).
Пример задачи Условие : докажите , что середины сторон прямоугольника являются вершинами ромба. Доказательство . Диагонали прямоугольника равны, поэтому середины сторон прямоугольника являются вершинами ромба (см.следствие 1: параллелограмм Вариньона является ромбом тогда и только тогда, когда в исходном четырехугольнике : диагонали равны
Пример задачи Условие : У четырехугольника диагонали равны a и b . Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника . Решение. Периметр параллелограмма Вариньона равен a + b .
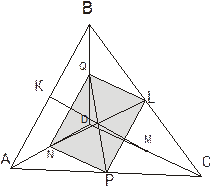
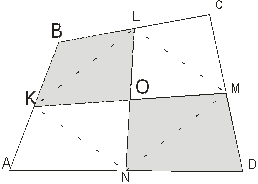
Пример задачи Условие : докажите, что площадь параллелограмма, образованного прямыми, проходящими через вершины выпуклого четырехугольника и параллельными его диагоналям, в два раза больше площади исходного четырехугольника (рис.).
Решение Так как AMOL , MONB , CKON , DKOL — параллелограммы, то Отсюда получаем , что , что и требовалось доказать.
Заключение. Тема работы посвящена бимедианам четырехугольника и теореме Вариньона. Эти замечательные понятия не входят в программу по геометрии для средней школы. Однако при решении целого класса задач эти понятия позволяют легко получить решение, в то время когда традиционные подходы приводят к громоздким и утомительным преобразованиям.
Видео:Математика для всех. Алексей Савватеев. Лекция 2.4. Теорема ЭйлераСкачать

Реферат: Бимедианы четырехугольника
| Название: Бимедианы четырехугольника Раздел: Рефераты по математике Тип: реферат Добавлен 13:27:38 12 июля 2011 Похожие работы Просмотров: 2012 Комментариев: 20 Оценило: 8 человек Средний балл: 5 Оценка: 5 Скачать | |||||||||||||||||||||||||||||||||||
|
|
а) Так как диагонали исходного четырехугольника равны, то стороны параллелограмма Вариньона будут равны (используя свойство средних линий треугольников, образованных при пересечении диагоналей исходного четырехугольника). Параллелограмм Вариньона является ромбом (по признаку ромба).
б) Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали перпендикулярны, то этот параллелограмм является ромбом (по признаку ромба).
2. Параллелограмм Вариньона является прямоугольником тогда и только тогда, когда в исходном четырехугольнике:
а) диагонали перпендикулярны(см. рис. 3,а);
б) бимедианы равны(см. рис. 3,б).
|
|
а) Так как диагонали исходного четырехугольника перпендикулярны, то стороны параллелограмма Вариньона будут перпендикулярны. Тогда параллелограмм Вариньона является прямоугольником (по признаку прямоугольника).
б) Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником (по признаку прямоугольника).
3. Параллелограмм Вариньона является квадратом тогда и только тогда, когда в исходном четырехугольнике:
а) диагонали равны и перпендикулярны(см. рис. 4,а);
б) бимедианы равны и перпендикулярны (см. рис. 4,б).
|
|
а) Так как диагонали исходного четырехугольника равны и перпендикулярны, то стороны параллелограмма Вариньона будут равны и перпендикулярны. Тогда параллелограмм Вариньона является квадратом (по признаку квадрата).
б) Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм является квадратом (по признаку квадрата).
Бимедианы четырехугольника и отрезок, соединяющий середины диагоналей, пересекаются в одной точке и делятся этой точкой пополам.
Пусть KM и LN – бимедианы ABCD, PQ – отрезок, соединяющий середины диагоналей АС и BD.
То, что бимедианы KM и LN точкой пересечения делятся пополам, следует из того, что эти отрезки являются диагоналями параллелограмма Вариньона. Поэтому нам достаточно доказать, что отрезки PQ и LN их точкой пересечения делятся пополам (рис.5, а и б; обращаем внимание на то, что в невыпуклом четырехугольнике одна из диагоналей расположена вне четырехугольника).
|
|
Используя теорему о средней линии треугольника для соответствующих треугольников, имеем:
Тем самым, PLQN – параллелограмм. По свойству параллелограмма следует, что отрезки PQ и LN их точкой пересечения делятся пополам. Что и требовалось доказать.
1.3.3. Следствие 3.(теорема Эйлера).
Для четырехугольника сумма квадратов всех сторон равна сумме квадратов диагоналей плюс учетверенный квадрат отрезка, соединяющего середины диагоналей, то есть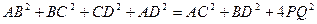
|
Уже было отмечено что LPNQ – параллелограмм (рис.6).
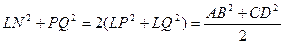
В последнем равенстве мы дважды воспользовались теоремой о средней линии треугольника. Аналогично для параллелограмма KPMQ имеем:
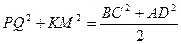
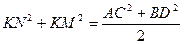
Так как KLMN – параллелограмм Вариньона четырехугольника ABCD . Складывая первые два равенства и учитывая последнее, получаем соотношение Эйлера.
1.3.4.Следствие 4.(теорема о бабочках).
Суммы площадей накрест лежащих четырехугольников, образованных пересечением бимедиан LN и KM выпуклого четырехугольника ABCD равны (рис. 7 ).
|
Воспользуемся теоремой о средней линии треугольника. Получаем:
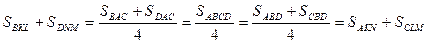
Что и требовалось доказать.
2.1.задачи из школьного курса геометрии.
Рассмотрим задачи на бимедианы четырехугольника и теорему Вариньона, которые встречаются в школьном курсе геометрии.
Докажите, что а) середины сторон прямоугольника являются вершинами ромба. И наоборот, б) середины сторон ромба являются вершинами прямоугольника.
а) Диагонали прямоугольника равны, поэтому середины сторон прямоугольника являются вершинами ромба (см.следствие 1, 1, а);
Стороны прямоугольника перпендикулярны, поэтому бимедианы перпендикулярны, тогда середины сторон прямоугольника являются вершинами ромба (см. следствие 1, 1, б).
б) диагонали ромба перпендикулярны, поэтому середины сторон ромба являются вершинами прямоугольника (см. следствие 1, 2, а);
Стороны ромба равны, поэтому середины сторон ромба являются вершинами прямоугольника (см. следствие 1, 2, б).
У четырехугольника диагонали равны a и b. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Периметр параллелограмма Вариньона равен a+ b .
Докажите, что середины сторон четырехугольника являются вершинами параллелограмма.
См. теорему Вариньона.
2.2. Конкурсные задачи.
Рассмотрим задачи на бимедианы четырехугольника и теорему Вариньона, которые взяты нами с различных математических конкурсов и олимпиад.
Пусть K, L, M, N – середины сторон выпуклого четырехугольника ABCD (см. рис. 8). Докажите, что
а) 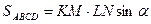
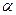
б) 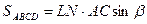
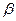
|
а) Так как ABCD — параллелограмм Вариньона, а KMи NL– бимедианы, то 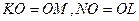
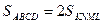
Докажите, что площадь параллелограмма, образованного прямыми, проходящими через вершины выпуклого четырехугольника и параллельными его диагоналям, в два раза больше площади исходного четырехугольника (рис.9).
|
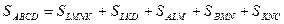
Так как AMOL, MONB, CKON, DKOL — параллелограммы, то 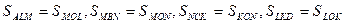
Отсюда получаем, что 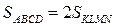
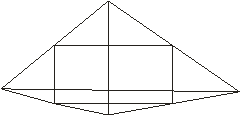
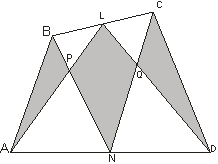
Все стороны выпуклого четырехугольника площади 1 разделены на 2n равных частей, а затем точки деления на противоположных сторонах соединены так, чтобы получилась «косоугольная шахматная доска», состоящая из белых и черных «клеток» (см. рис. при n= 2). Доказать, что сумма площадей всех белых «клеток» равна сумме площадей всех черных «клеток» (рис.10).
|
Из следствия 2 следует, что точки пересечения отрезков на этой доске делят каждый на равные части.
Тогда в любом «маленьком» четырехугольнике (рис.10),куда входят ровно две белые и две черные клетки, выполняются условия теоремы о бабочках. Нужное равенство установлено.
На продолжениях сторон выпуклого четырехугольника ABCD выбраны точки 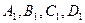
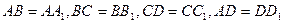
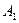
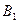
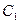
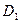
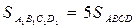
|
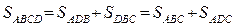
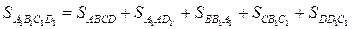
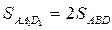
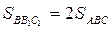
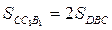
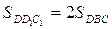
Отсюда получаем, что 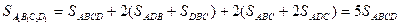
Пусть L и N – середины противоположных сторон BC и AD четырехугольника ABCD (рис. 12). Доказать, что площадь четырехугольника LPNQ равна сумме площадей треугольников ABP и CQD .
|
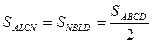
В треугольникеACD медиана CN делит его на два треугольника равной площади, а в треугольнике ABC медиана AL делит его на два равновеликих треугольника. Так как 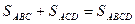
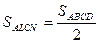
Теперь утверждение задачи следует из того, что четырехугольники ALCN и NBLD покрывают внутри четырехугольника ABCD два раза четырехугольник LPNQ и не покрывают треугольники ABP иCQD , а их сумма их площадей равна площади четырехугольника ABCD. Площадь четырехугольника, с другой стороны, равна сумме площадей шести треугольников (в том числе и треугольников ABP и CQD ) и интересующего нас четырехугольника LPNQ .
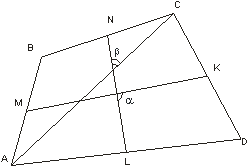
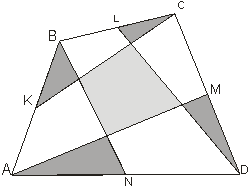
Пусть K, L, M, N – середины сторон (рис. 13) выпуклого четырехугольника ABCD . Докажите, что площадь четырехугольника, образованного прямыми CK, AM, BN, DL, равна сумме площадей четырех треугольников, отмеченных на рисунке 6.
|
Так как 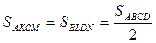
Противоположные стороны четырехугольника ABCD разделены на три равные части и точки деления попарно соединены (рис.14). Доказать, что одна из площадей получившихся трех четырехугольников равна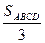
|
Докажем, что площадь среднего четырехугольника равна трети площади исходного четырехугольника. Другими словами докажем, что
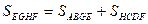
Чтобы в этом убедиться, достаточно проверить, что
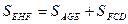
А последнее равенство есть следствие того, что основания AE, EF, FD всех трех треугольников в этом равенстве равны, а высота треугольника EHF является средней линией трапеции с основаниями, равными высотам треугольников AGE и FCD.
Отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника ABCD ,перпендикулярны (Рис.15) . Известно, что

Найдите площадь четырехугольника ABCD и сравните её с числом 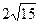
|
Так как бимедианы перпендикулярны, то параллелограмм Вариньона является ромбом (см.следствие1,1,б).
Так как KN является средней линией треугольника ADC , то по теореме о средней линии треугольника KN=0,5 AC=2 ;
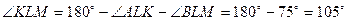
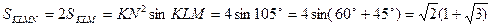
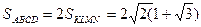
Площадь ABCD меньше, чем 2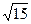
Отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника ABCD ,перпендикулярны (Рис.15) . Известно, что
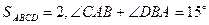
Найдите квадрат длины отрезка PR и сравните его с числом 4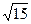
Пусть KLMN – параллелограмм Вариньона четырехугольника ABCD .
Так как бимедианы перпендикулярны, то параллелограмм Вариньона является ромбом (см. следствие1,1,б).
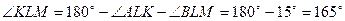
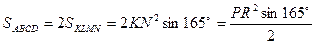
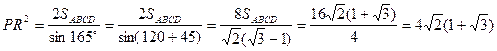
1. Погорелов А. В. Геометрия: Учеб. для 7 – 11 кл. сред. шк.- М.: Просвещение,1990.- 384 с.
2. Штейнгауз Г.Математический калейдоскоп. – М.:наука,1981.
3. Прасолов В.В. задачи по планиметрии. – Т.1, 2. – М.: Наука,1995.
4. Коксетер Г. С. М., Грейтцер С.Л. Новые встречи с геометрией. – М.: Наука,1978.
5. В. Вавилов, П. Красников. Бимедианы четырехугольника//Математика. 2006 — №22.
📸 Видео
Теорема Эйлера | Доказательство.Скачать

Функция ЭйлераСкачать

✓ Формула Эйлера для графов и многогранников за 8 минут | Ботай со мной #103 | Борис ТрушинСкачать

10 класс, 29 урок, Теорема ЭйлераСкачать

Графы. Теорема ЭйлераСкачать

Теоремы Эйлера и Ферма + задача с древнего IMO | Олимпиадная математикаСкачать

Функция Эйлера | Теория чиселСкачать

06. Формула ЭйлераСкачать

#161. САМАЯ КРАСИВАЯ ФОРМУЛА В МАТЕМАТИКЕ — ФОРМУЛА ЭЙЛЕРА: e^(iπ)+1=0Скачать

Эйлеров цикл. Эйлеров граф. Теорема об эйлеровых графахСкачать

8 класс, 3 урок, ЧетырехугольникСкачать

#58. Олимпиадная задача о четырехугольникеСкачать

Произвольный четырехугольникСкачать

11 класс, 49 урок, Задача ЭйлераСкачать

Функция ЭйлераСкачать

#205. Формула Эйлера для плоских графов: В-Р+Г=2 | Платоновы тела (feat. Борис Трушин)Скачать