 Формулы для площадей четырехугольников Формулы для площадей четырехугольников |
 Вывод формул для площадей четырехугольников Вывод формул для площадей четырехугольников |
 Вывод формулы Брахмагупты для площади вписанного четырехугольника Вывод формулы Брахмагупты для площади вписанного четырехугольника |
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.
- Формулы для площадей четырехугольников
- Вывод формул для площадей четырехугольников
- Решение геометрических задач по готовым чертежам
- «Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Оставьте свой комментарий
- Подарочные сертификаты
- Площадь четырехугольника
- Площадь четырехугольника по диагоналям и углу между ними
- Площадь четырехугольника через стороны и углы между этими сторонами
- Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты
- Площадь четырехугольника в который можно вписать окружность
- Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними
- Таблица с формулами площади четырехугольника
- Площадь частных случаев четырехугольников
- Определения
- 📺 Видео
Видео:№517. Найдите площадь четырехугольника ABCD, в котором АВ = 5 см, ВС = 13 см, CD = 9 см, DA =15 смСкачать
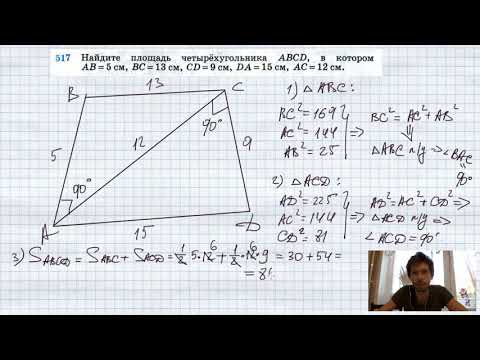
Формулы для площадей четырехугольников
| Четырехугольник | Рисунок | Формула площади | Обозначения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прямоугольник |  | S = ab | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Параллелограмм |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Квадрат |  | S = a 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | S = 4r 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ромб |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Трапеция |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | S = m h | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дельтоид |  | S = ab sin φ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Произвольный выпуклый четырёхугольник |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вписанный четырёхугольник |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прямоугольник | |||||||||||||||||||||
 | |||||||||||||||||||||
 | |||||||||||||||||||||
 | |||||||||||||||||||||
| Параллелограмм | |||||||||||||||||||||
 | |||||||||||||||||||||
 | |||||||||||||||||||||
 | |||||||||||||||||||||
| Квадрат | |||||||||||||||||||||
 | S = a 2 где | ||||||||||||||||||||
 | S = 4r 2 | ||||||||||||||||||||
 | |||||||||||||||||||||
 | |||||||||||||||||||||
| Ромб | |||||||||||||||||||||
 | |||||||||||||||||||||
 | |||||||||||||||||||||
 | |||||||||||||||||||||
 | |||||||||||||||||||||
 | |||||||||||||||||||||
| Трапеция | |||||||||||||||||||||
 | |||||||||||||||||||||
 | |||||||||||||||||||||
 | |||||||||||||||||||||
 | |||||||||||||||||||||
| Дельтоид | |||||||||||||||||||||
 | |||||||||||||||||||||
 |  где | ||||||||||||||||||||
 | |||||||||||||||||||||
 | |||||||||||||||||||||
| Произвольный выпуклый четырёхугольник | |||||||||||||||||||||
 | |||||||||||||||||||||
| Вписанный четырёхугольник | |||||||||||||||||||||
 | |||||||||||||||||||||
| Прямоугольник |
 |
где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R

где
a – сторона,
ha – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

где
a – сторона квадрата



Получается из верхней формулы подстановкой d = 2R

где
a – сторона,
ha – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба



где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

где
a и b – основания,
h – высота


φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны ,

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .

где
a и b – неравные стороны,
r – радиус вписанной окружности


φ – любой из четырёх углов между ними

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
Видео:Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать

Вывод формул для площадей четырехугольников
Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле
Доказательство . В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле
где a – сторона параллелограмма, а ha – высота высота высота , опущенная на эту сторону (рис. 2).
Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
что и требовалось доказать.
Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
то, в силу утверждения 2, справедлива формула
что и требовалось доказать.
Утверждение 4 . Площадь ромба ромба можно найти по формуле

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
что и требовалось доказать.
Утверждение 5 . Площадь трапеции можно найти по формуле

где a и b – основания трапеции, а h – высота высота высота (рис.5).
Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому
что и требовалось доказать.
Утверждение 6 . Площадь трапеции трапеции можно найти по формуле
где a и b – основания, а c и d – боковые стороны трапеции ,
(рис.6).
Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

что и требовалось доказать.
Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
Видео:Площадь прямоугольника. Как найти площадь прямоугольника?Скачать

Решение геометрических задач по готовым чертежам
Видео:ПЛОЩАДЬ ЧЕТЫРЕХУГОЛЬНИКА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
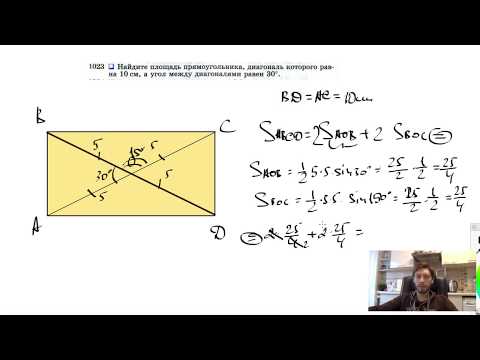
Видео:№1023. Найдите площадь прямоугольника, диагональ которого равна 10 см, а уголСкачать
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Площадь четырехугольника Решение треугольников 9-10 класс МБОУ Гимназия№4 г. Новосибирска Баринова Людмила Леонидовна учитель высшей квалификационной категории
Площадь четырехугольников Задача 1 Найти площадь ABCD по данным чертежа; ABCD – параллелограмм
Площадь четырехугольников Задача 1 Найти площадь ABCD по данным чертежа; ABCD – параллелограмм Д.п. — высота BH. ∆ABH: угол H=90° Теорема синусов: AB/sinH=BH/sinA
Площадь четырехугольников Задача 2 Найти площадь ABCD по данным чертежа; ABCD – параллелограмм
Площадь четырехугольников Задача 2 Найти площадь ABCD по данным чертежа; ABCD – параллелограмм ∆BAE: угол E=90° По теореме Пифагора AB2=AE2+BE2 S=BE•AD=12•3=36
Площадь четырехугольников Задача 3 Найти площадь ABCD по данным чертежа; ABCD – параллелограмм
Площадь четырехугольников Задача 3 Найти площадь ABCD по данным чертежа; ABCD – параллелограмм ∆CBF: угол F=90° S=BE•BC=8•5=40
Площадь четырехугольников Задача 4 Найти площадь ABCD по данным чертежа; ABCD – параллелограмм
Площадь четырехугольников Задача 4 Найти площадь ABCD по данным чертежа; ABCD – параллелограмм
Площадь четырехугольников Задача 5 Найти площадь ABCD по данным чертежа; ABCD – ромб
Площадь четырехугольников Задача 5 Найти площадь ABCD по данным чертежа; ABCD – ромб BD=2BO=5•2=10 ∆AOB: угол O=90°
Площадь четырехугольников Задача 6 Найти площадь ABCD по данным чертежа; ABCD – ромб
Площадь четырехугольников Задача 6 Найти площадь ABCD по данным чертежа; ABCD – ромб ∆ABE: угол E=90°
Площадь четырехугольников Задача 7 Найти площадь ABCD по данным чертежа; ABCD – ромб
Площадь четырехугольников Задача 7 Найти площадь ABCD по данным чертежа; ABCD – ромб ∆ABD –равносторонний : угол A=B=C=60°
Площадь четырехугольников Задача 8 Найти площадь ABCD по данным чертежа;ABCD – ромб;O – центр вписанной окружности.
Площадь четырехугольников Задача 8 Найти площадь ABCD по данным чертежа;ABCD – ромб;O – центр вписанной окр. OE – радиус вписанной окружности ∆OED: угол E=90°
Площадь четырехугольников Задача 9 Найти площадь трапеции ABCD по данным чертежа
Площадь четырехугольников Задача 9 Найти площадь трапеции ABCD по данным чертежа
Площадь четырехугольников Задача 10 Найти площадь трапеции ABCD по данным чертежа
Площадь четырехугольников Задача 10 Найти площадь трапеции ABCD по данным чертежа Д.п. — высоты BH и СH1 HH1=BC=7 ∆ABH: угол H=90°
Площадь четырехугольников Задача 11 Найти площадь трапеции ABCD по данным чертежа
Площадь четырехугольников Задача 11 Найти площадь трапеции ABCD по данным чертежа Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Площадь четырехугольников Задача 12 Найти площадь трапеции ABCD по данным чертежа;O – центр вписанной окружности.
Площадь четырехугольников Задача 12 Найти площадь трапеции ABCD по данным чертежа;O – центр вписанной окр. Если в трапецию вписана окружность радиуса r, и она делит боковую сторону точкой касания на два отрезка a и b, то справедливо следующее равенство: BC=4+6=10 AD=9+6=15(свойство отрезков касательных) CD=2r=6•2=12
Решение треугольников Задача 1 Найти неизвестные стороны и углы треугольника ABC по данным чертежа
Решение треугольников Задача 1 Найти неизвестные стороны и углы треугольника ABC по данным чертежа
Решение треугольников Задача 2 Найти неизвестные стороны и углы треугольника ABC по данным чертежа
Решение треугольников Задача 2 Найти неизвестные стороны и углы треугольника ABC по данным чертежа
Решение треугольников Задача 3 Найти неизвестные стороны и углы треугольника ABC по данным чертежа
Решение треугольников Задача 3 Найти неизвестные стороны и углы треугольника ABC по данным чертежа
Решение треугольников Задача 4 Найти неизвестные стороны и углы треугольника ABC по данным чертежа
Решение треугольников Задача 4 Найти неизвестные стороны и углы треугольника ABC по данным чертежа AB=AC=R →∆ABC-равнобедренный
Решение треугольников Задача 5 Найти неизвестные стороны и углы треугольника ABC по данным чертежа
Решение треугольников Задача 5 Найти неизвестные стороны и углы треугольника ABC по данным чертежа
Решение треугольников Задача 6 Найти неизвестные стороны и углы треугольника ABC по данным чертежа
Решение треугольников Задача 6 Найти неизвестные стороны и углы треугольника ABC по данным чертежа ∆ADC-равнобедренный
Решение треугольников Задача 7 Найти неизвестные стороны и углы треугольника ABC по данным чертежа
Решение треугольников Задача 7 Найти неизвестные стороны и углы треугольника ABC по данным чертежа
Решение треугольников Задача 8 Найти неизвестные стороны и углы треугольника ABC по данным чертежа
Решение треугольников Задача 8 Найти неизвестные стороны и углы треугольника ABC по данным чертежа ∆ABC-равнобедренный ∆DOC: OD=r
Решение треугольников Задача 9 Найти неизвестные стороны и углы треугольника ABC по данным чертежа
Решение треугольников Задача 9 Найти неизвестные стороны и углы треугольника ABC по данным чертежа
Решение треугольников Задача 10 Найти радиус описанной около треугольника ABC окружности по данным чертежа
Решение треугольников Задача 10 Найти радиус описанной около треугольника ABC окружности по данным чертежа
Решение треугольников Задача 11 Найти радиус описанной около треугольника ABC окружности по данным чертежа
Решение треугольников Задача 11 Найти радиус описанной около треугольника ABC окружности по данным чертежа ∆ABC-равнобедренный
Решение треугольников Задача 12 Найти радиус описанной около треугольника ABC окружности по данным чертежа
Решение треугольников Задача 12 Найти радиус описанной около треугольника ABC окружности по данным чертежа ABCD-равнобедренная трапеция
Решение треугольников Задача 12 Найти радиус описанной около треугольника ABC окружности по данным чертежа ∆ABC-равнобедренный ABCD-равнобедренная трапеция
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 967 человек из 79 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 340 человек из 71 региона
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 691 человек из 74 регионов
Ищем педагогов в команду «Инфоурок»
- Баринова Людмила ЛеонидовнаНаписать 32663 01.04.2014
Номер материала: 53057040136
- 01.04.2014 7969
- 01.04.2014 12422
- 01.04.2014 733
- 01.04.2014 823
- 01.04.2014 2571
- 01.04.2014 2654
- 01.04.2014 584
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Госдуме предложили продлить каникулы для школьников до 16 января
Время чтения: 1 минута
Правительство направит регионам почти 92 миллиарда рублей на ремонт и оснащение школ
Время чтения: 1 минута
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
В России разработают рекомендации по сопровождению студентов с ОВЗ
Время чтения: 2 минуты
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Глава СПЧ предложил ввести подготовительные курсы перед обучением в школе для детей мигрантов
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Рабинович Е. М. Геометрия 7-9 классы. Таблица 9.10 "Площадь четырёхугольника".Скачать

Площадь четырехугольника
Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн. Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.
В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.
Видео:Площадь четырехугольникаСкачать

Площадь четырехугольника по диагоналям и углу между ними
Видео:Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Площадь четырехугольника через стороны и углы между этими сторонами
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Видео:8 класс, 12 урок, Площадь прямоугольникаСкачать

Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты
Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Видео:Площади фигур. Сохраняй и запоминай!#shortsСкачать

Площадь четырехугольника в который можно вписать окружность
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Видео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Видео:Задача с канала PreMath — попробуй найти площадь четырехугольникаСкачать

Таблица с формулами площади четырехугольника
| исходные данные (активная ссылка для перехода к калькулятору) | эскиз | формула | |
| 1 | диагональ и угол между ними |  | |
| 2 | стороны и углы между этими сторонами |  | |
| 3 | стороны (по Формуле Брахмагупты) |  | |
| 4 | стороны и радиус вписанной окружности |  | |
| 5 | стороны и углы между ними |  |
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Площадь частных случаев четырехугольников
Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:
Определения
Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь четырехугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.
Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.
📺 Видео
Найдите площадь четырёхугольникаСкачать

Площадь четырёхугольника через диагоналиСкачать

Площади четырехугольников: трапеция, параллелограмм, ромб. Геометрия на клеточке. ОГЭСкачать

Геометрия 8. Урок 13 - Площадь четырехугольников. ЗадачиСкачать

Вирусная задача. Найти площадь четырёхугольника.Скачать
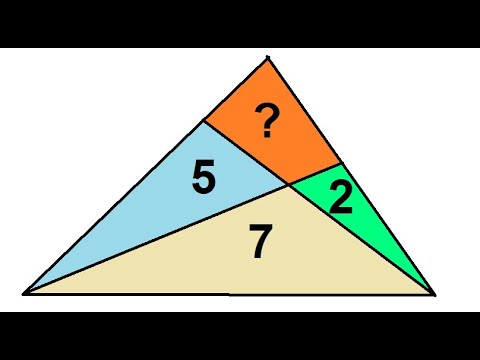
№1020. Найдите площадь треугольника ABC, если: а) АВ = = 6√8 см, АС=4 см, ∠А=60°;Скачать
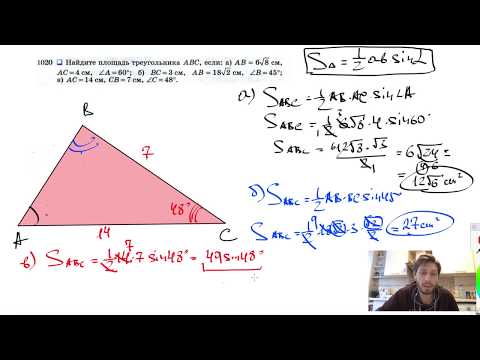
Самый простой способ нахождения площадиСкачать






 ,
,






























