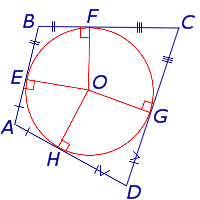
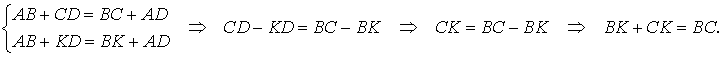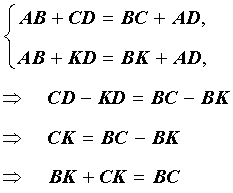Определение 1 . Окружностью, вписанной в четырёхугольник, называют окружность, которая касается касается каждой из сторон четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, описанным около окружности или описанным четырёхугольником .
Замечание . В настоящем разделе мы рассматриваем только выпуклые четырёхугольники.
Теорема 1 . Если четырёхугольник описан около окружности, то суммы длин его противоположных сторон равны.
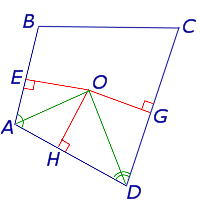
Доказательство . Рассмотрим четырёхугольник ABCD , описанный около окружности, и обозначим буквами E, F, G, H – точки касания сторон четырёхугольника с окружностью (рис.2).
AH = AE, BF = BE, CF = CG, DH = DG,
Складывая эти равенства, получим:
AH + BF + CF + DH =
= AD + BC,
AE + BE + CG + DG =
= AB + CD,
то справедливо равенство
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1) . Если у четырёхугольника суммы длин противоположных сторон равны, то в этот четырёхугольник можно вписать окружность.
Доказательство . Рассмотрим четырёхугольник ABCD , длины сторон которого удовлетворяют равенству
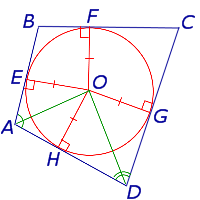
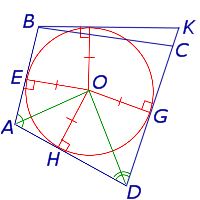
и проведём биссектрисы углов BAD и CDA . Обозначим точку пересечения этих биссектрис буквой O , и опустим из точки O перпендикуляры OH, OE и OG на стороны AD, AB и CD соответственно (рис.3).
Следовательно, справедливы равенства
из которых вытекает, что точки H, E и G лежат на окружности с центром в точке O и радиусом OH , касающейся сторон четырёхугольника AD, AB и CD в точках H, E и G соответственно. При этом возможны два случая:
Окружность касается касается стороны BC (рис.4).
В этом случае четырёхугольник ABCD описан около окружности, и теорема доказана.
Окружность не касается стороны BC .
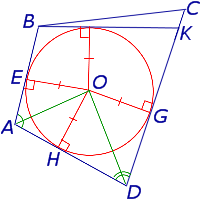
В этом случае касательная, проведенная к окружности из точки B , пересекает прямую DC в точке K , и возможны два случая:
- Точка K лежит между точками C и D (рис.5)
Рассмотрим случай 2а и приведём его к противоречию. В этом случае в силу того, что четырёхугольник ABKD является описанным, а также по условию теоремы справедливы равенства:
Последнее равенство утверждает, что в треугольнике BKC сумма двух сторон равна третьей стороне, что противоречит неравенству треугольника неравенству треугольника неравенству треугольника . Полученное противоречие доказывает, что случай 2а невозможен.
Совершенно аналогичные рассуждения позволяют заключить, что случай 2b также невозможен.
Итак, возможен и реализуется лишь случай 1.
Из доказательства теоремы 2 непосредственно вытекает
Теорема 3 . Биссектрисы всех внутренних углов описанного четырёхугольника пересекаются в одной точке – центре вписанной окружности.
В следующей таблице приводятся примеры четырёхугольников, в которые можно вписать окружность. Доказательства утверждений непосредственно вытекают из теорем 1 и 2 и предоставляются читателю в качестве несложных упражнений.
Примеры описанных четырёхугольников
| Фигура | Рисунок | Утверждение |
| Ромб | 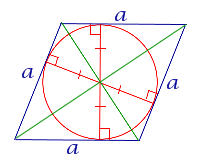 | В любой ромб можно вписать окружность |
| Квадрат | 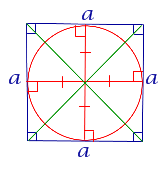 | В любой квадрат можно вписать окружность |
| Прямоугольник | 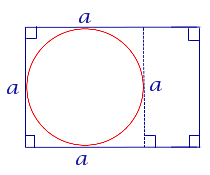 | В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом |
| Параллелограмм | 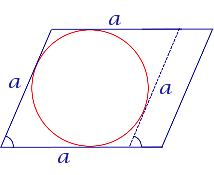 | В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом |
| Дельтоид | 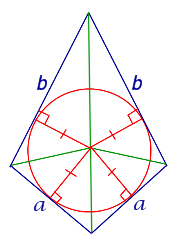 | В любой дельтоид можно вписать окружность |
| Трапеция | 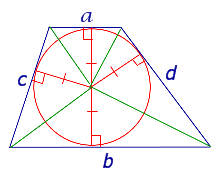 | В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон рана сумме длин оснований |
| Ромб |
 |

В любой квадрат можно вписать окружность

В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом

В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом


В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон рана сумме длин оснований
Видео:Свойство и признак описанного четырехугольникаСкачать

Свойства и признаки описанного четырехугольника.
Описанный четырехугольник — четырехугольник, все стороны которого касаются окружности.
Центр вписанной окружности в четырехугольник — точка пересечения биссектрис всех углов четырехугольника. Не все четырёхугольники можно описать около окружности, так как биссектрисы четырёх углов могут не пересекаться в одной точке.
Основной признак описанного четырехугольника:
Если суммы противоположных сторон четырехугольника равны, то четырехугольник является описанным.
Основное свойство описанного четырехугольника:
Если четырехугольник является описанным, то суммы противоположных сторон этого четырехугольника равны.
Видео:Свойство и признак вписанного четырехугольникаСкачать

Вписанный и описанный четырехугольник
Видео:Свойство и признак описанного четырехугольникаСкачать

Вписанный четырехугольник
Если все вершины четырехугольника лежат на одной окружности, то он называется вписанным четырехугольником .
В отличие от треугольника не всякий четырехугольник является вписанным.
Критерий вписанного четырехугольника
Сумма противолежащих углов четырехугольника равна 1 8 0 ∘ 180^ 1 8 0 ∘ тогда и только тогда, когда он вписанный.
Свойства вписанного четырехугольника:
Видео:3 правила для вписанного четырехугольника #shortsСкачать

Описанный четырехугольник
Если все стороны четырехугольника касаются некоторой окружности , то он называется описанным четырехугольником .
Признак описанного четырехугольника
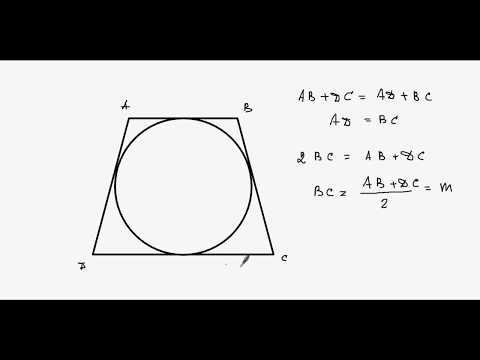
Суммы длин противолежащих сторон описанного четырехугольника равны: a + c = b + d a+c=b+d a + c = b + d .
🎥 Видео
Свойства и признаки вписанного четырехугольникаСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Свойство описанного четырёхугольникаСкачать

свойства вписанного и описанного четырехугольника #SHORTSСкачать
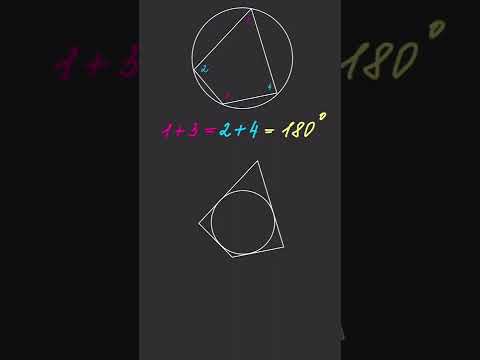
Свойство и признак вписанного четырехугольникаСкачать
ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

2 ПРАВИЛА описанного четырехугольника #shortsСкачать

Свойство описанного четырехугольника #огэ #математика #огэматематика #данирСкачать

Свойство сторон описанного четырёхугольника.Скачать
Геометрия. Признак описанного четырехугольника.Скачать

Описанный четырехугольник ✧ Его свойства и признак ✧ Запомнить за 1 мин!Скачать

Функция. Область определения функции. Практическая часть. 10 класс.Скачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

11 класс, 44 урок, Описанный четырехугольникСкачать

ОГЭ Задание 25 Свойства вписанного и описанного четырехугольникаСкачать