Свойства собственных векторов собственных значений

СВОЙСТВА СОБСТВЕННЫХ ВЕКТОРОВ И СОБСТВЕННЫХ ЗНАЧЕНИЙ ЛИНЕЙНОГО ОПЕРАТОРА

Высшая математика

— Собственные значения λ _i являются корнями характеристического уравнения det( A −λ E ) = 0.

— Оператор A (матрица A ) имеет не более n различных собственных значений.

— Собственные значения матриц A и A T совпадают.

— Если матрица A обратима, то все её собственные значения отличны от нуля, λ _i≠ 0; при этом собственными значениями обратной матрицы A − 1 являются числа (λ _i) − 1 , а соответствующие собственные векторы совпадают.

— Если число λ — собственное значение матрицы A, то собственным значением матрицы A k является число λ k , а соответствующие собственные векторы совпадают.

— Собственные значения подобных матриц A и C − 1 ·A·C совпадают. Здесь C — невырожденная матрица.

— Собственный вектор, отвечающий собственному значению λ _i является ненулевым решением линейной однородной системы ( A −λ E )· x = 0 , x≠ 0, x ∈ X .

— Собственные векторы, отвечающие различным собственным значениям, линейно независимы.

— Если линейный оператор A имеет n различных собственных значений, то соответствующие собственные векторы образуют базис пространства X , который называется собственным базисом линейного оператора.

— Если линейный оператор имеет собственный базис, то матрица оператора в собственном базисе имеет диагональный вид; диагональными элементами являются собственные значения оператора.

— Собственные векторы, отвечающие различным собственным значениям, ортогональны.

3.6. Собственные векторы и собственные значения линейного оператора

Пусть линейный оператор 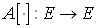. Ненулевой вектор называется Собственным вектором линейного оператора , если

. (10)

Число называется Собственным значением линейного оператора. Совокупность всех собственных значений называется Спектром линейного оператора . Спектр простой, если все собственные значения линейного оператора кратности 1.

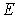
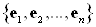
Рассмотрим в произвольный базис , в котором . Пусть в этом базисе линейному оператору соответствует матрица , тогда равенство (10) в матричной форме примет вид

(11)

Перейдём к системе из 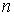уравнений:

(12)

Однородная СЛАУ (12) в матричной форме примет вид:

(13)

Она имеет ненулевые решения только в том случае, если её определитель равен нулю, т. е. если

(14)

Представим равенство (14) в виде:

. (15)

Уравнение (15) называется Характеристическим уравнением линейного оператора . Таким образом, собственные значения линейного оператора являются корнями его характеристического уравнения.

Уравнение (15) – алгебраическое уравнение -й степени относительно , значит, оно имеет ровно корней, действительных или комплексных, с учётом их кратности. Ясно, что в алгебраическом уравнении с вещественными коэффициентами всякий комплексный корень имеет комплексно-сопряжённый.

При нахождении собственных векторов соответствующие им векторы-столбцы определяют из системы (13) подстановкой в неё последовательно всех найденных собственных значений . При этом отметим, что в вещественном линейном пространстве комплексные корни характеристического уравнения нельзя рассматривать как собственные значения, так как умножение на комплексный скаляр в вещественном пространстве является запрещённой операцией.

Перечислим без доказательств некоторые свойства собственных значений и собственных векторов Линейных операторов.

Свойство 1. Характеристическое уравнение и спектр линейного оператора инвариантны относительно выбора базиса, т. е. подобные матрицы имеют одинаковый спектр.

Свойство 2. Собственные векторы линейного оператора, отвечающие различным собственным значениям, линейно независимы.

Свойство 3. Линейный оператор имеет собственное значение только в том случае, если он вырожденный, т. е. , где – матрица линейного оператора .

Свойство 4. Самосопряжённый линейный оператор имеет только действительные собственные значения;

Свойство 5. Собственные векторы самосопряжённого линейного оператора, отвечающие различным собственным значениям, ортогональны.

Свойство 6. Для произвольного самосопряжённого линейного оператора существует ортогональный базис, составленный из собственных векторов.

Самосопряженные преобразования евклидовых пространств, свойства их собственных значений и собственных векторов

Самосопряженные преобразования евклидовых пространств, свойства их собственных значений и собственных векторов

Определение 1. Линейное преобразование φ: E→E евклидова пространства E называется самосопряженным, если для любых x, y из E верно равенство (φ(x),y) = (x, φ(y)).

Свойства самосопряженных преобразований.

Пусть φ – самосопряженное преобразование евклидова пространства E. Тогда:

Утв.1. Если U – подпространство в E, инвариантное относительно φ (короче, φ — инвариантное подпространство) (т. е. ), то ортогональное дополнение также φ — инвариантно.

Доказательство. Для любых векторов , так как , следовательно, .

Замечание. Ограничение самосопряженного преобразования на инвариантное подпространство является самосопряженным, если на подпространстве рассматривать скалярное произведение, заданное во всем пространстве.

Утв.2. Собственные векторы , отвечающие различным собственным значениям, ортогональны.

Доказательство. Еcли φ(x1) = λ1×1, φ (x2) = λ2×2, x1 ≠ 0 ≠ x2, причем λ1≠ λ2, то □ .

Утв. 3. В ортонормированном базисе (о. н.б.) матрица A самосопряженного преобразования φ является симметрической: AT = A.

Доказательство. Если – ортонормированный базис в V, , – столбец координат вектора x, – строка его координат, то . Тогда

так что .

Так как для любых i, j от 1 до n (где – i-й столбец единичной матрицы), то , то есть AT = A. □

В доказательстве свойства собственных значений понадобится

Лемма. Любое линейного преобразование конечномерного действительного линейного пространства обладает одномерным или двумерным инвариантным подпространством U. (Одномерное порождено собственным вектором, а двумерное соответствует комплексному (не вещественному) характеристическому корню.)

Теорема 1. Все характеристические корни ( корни характеристического уравнения) самосопряженного преобразования (или симметрической матрицы) действительные.

Доказательство проводится индукцией по n=dim E.

Случай n =1 очевиден. При n = 2 в ортонормированном базисе

= 0. Дискриминант этого уравнения , следовательно, .

При n > 2 сделаем индуктивное предположение о том, что у любой симметрической матрицы порядка 1 пусть – какой-либо характеристический корень (действительный, по теореме 1), h1 соответствующий собственный вектор (можно сразу взять ) и – одномерное инвариантное подпространство. Согласно утв.1, инвариантно размерности n–1, и для ограничения преобразования на , по предположению индукции, существует ортонормированный базис из собственных векторов. Тогда – искомый базис.

□Пример. В некотором о. н.б. в R3 линейное преобразование φ задано матрицей . Найти для φ ортонормированный базис из собственных векторов и записать в нем матрицу преобразования.

□

Собственные векторы: , . Система уравнений для собственных векторов: , так что имеются два линейно независимых собственных вектора. Можно взять Второй линейно независимый собственный вектор ищем ортогональный к h1, т. е. как решение системы . Например, , т. е.

Собственный вектор для , по утв. 2, ортогонален к , так что в трехмерном пространстве он единственный с точностью до множителя вектор из . Читая уравнение как скалярное произведение , без вычислений находим (Разумеется, можно было решить характеристическую систему уравнений для и получить то же самое.)

Окончательно, нормируя, получаем . В этом базисе .□

Можно упомянуть 2 типичных примера самосопряженных преобразований.

Пусть E – n-мерное евклидово пространство, U – подпространство в E, 0 ≠ U ≠ V, тогда любой вектор единственным образом представляется в виде .

Пример 1. Ортогональное проектирование V на U: . Проверка самосопряженности: . Ядром преобразования является U.

Собственные векторы: . В о. н.б., составленном из базисов подпространств U, , матрица преобразования равна , если .

Пример 2. Ортогональная симметрия (или зеркальное отражение) S пространства E относительно U: S(x) = y – z. Проверить самосопряженность можно аналогично.

Собственные векторы: . В о. н.б., составленном из базисов подпространств U, , матрица оператора равна .

🔍 Видео