Сумма векторов и не зависит от точки a (5 видео)

Сложение и вычитание векторов

Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .

Существование: Имеем два следующих случая:

Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .

Из данного выше построения сразу же будет следовать единственность данного вектора.

Содержание

Сумма векторов. Сложение векторов. Правило треугольника
Разность векторов. Вычитание векторов
Умножение вектора на число
Геометрия
Укажи вектор, равный сумме двух векторов
Урок «Сложение и вычитание векторов»
📸 Видео

Видео:Сложение векторов. 9 класс.Скачать

Сумма векторов. Сложение векторов. Правило треугольника

Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.

Суммой нескольких векторов ( vec ) , ( vec ) , ( vec ,;ldots ) называется вектор ( vec ) , получающийся в результате последовательного сложения данных векторов.

Такая операция выполняется по правилу многоугольника.

Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( <+ , + , + > right) )

Отметим несколько свойств сложения двух векторов:

Для произвольного вектора ( overrightarrow ) выполняется равенство

Для произвольных точек ( A, B и C ) справедливо следующее равенство

Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Разность векторов. Вычитание векторов

Разность двух одинаковых векторов равна нулевому вектору :
( vec — vec = vec )

Длина нулевого вектора равна нулю:
( left| vec right| = 0 )

Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec — vec = left( <- , — , — > right) )

Видео:Сложение векторов. Правило параллелограмма. 9 класс.Скачать

Умножение вектора на число

Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .

Определение Произведением вектора ( overrightarrow ) на действительное число ( k ) называется вектор ( overrightarrow ) удовлетворяющий следующим условиям:

Длина вектора ( overrightarrow ) равна ( left|overrightarrowright|=left|kright||overrightarrow| ) ;

Векторы ( overrightarrow ) и ( overrightarrow ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )

Обозначение: ( overrightarrow=koverrightarrow ) .

Видео:Вычитание векторов. 9 класс.Скачать

Геометрия

УРОК: «СЛОЖЕНИЕ ВЕКТОРОВ»

Тема: Сложение векторов

Класс: 9 класс
Педагог: , заместитель директора по воспитательной работе, учитель математики и информатики.

Учреждение образования: МОУ Шуринская средняя общеобразовательная школа Кемеровской области
Город: Кемеровская область

Знать, как находится сумма двух и нескольких векторов, законы сложения векторов; какие векторы называются противоположными.

Уметь строить сумму данных векторов, пользуясь правилом треугольника и параллелограмма, применять правила при решении задач.

I. Организационный момент: объяснить цели урока

II. Проверка пройденного материала:

1. Верно ли утверждение:

Если = , то и коллинеарны

2. № 000 (б). Определите вид четырехугольника АВСD, если:

, а векторы и не коллинеарны. (трапеция)

В параллелограмме АВСD диагонали пересекаются в точке О. Равны ли векторы и

III. Объяснение нового материала

План объяснения

1. Противоположные векторы

Два вектора, имеющие равные модули и противоположные направления, называются противоположными.

Вектор, противоположный вектору , обозначается (- ) и (произносится «минус »).

На рисунке изображены противоположные векторы и , т. е. ½½=½ ½и . Если =, то = —

2. Правило треугольника

Если переместить тело из точки А в точку В, а потом из точки В в точку С (Рисунок1), то суммарное перемещение из А в С представляется вектором . Так складывают векторы и :

+ =

В рассмотренном случае конец первого вектора является началом второго вектора . В общем случае векторы и складываются следующим образом ( рисунок справа). Сначала откладывают от какой-либо точки А вектор = , а потом от точки В вектор=. Тогда вектор представляет сумму векторов и : + = + =

3. Сумма двух векторов.

Итак, суммой двух векторов называется вектор, построенный по правилу треугольника.

В частности, если вектор складывается с противоположным ему вектором (-), то в сумме получается нулевой вектор: + (-) = 0. Складывая векторы и по правилу треугольника, мы поступали так:

Выбирали точку А, откладывали от нее =, затем от точки В откладывали вектор = и получали вектор = +. Покажем, что полученный таким образом результат, т. е. сумма векторов и не зависит от выбора точки А. Для этого выберем какую-нибудь точку А1, отличную от точки А. По правилу треугольника построили векторы = и = .Требуется проверить, что векторы и АС равны. Действительно, т. к. = и =, то =, тогда АВВ1А1 — параллелограмм, отсюда АА1 = ВВ1. Аналогично из векторного равенства = вытекает, что = . Тогда т. к. два вектора и равны третьему вектору, то =. Следовательно, АСС1А1 — параллелограмм, отсюда =

При сложении векторов и имеют место следующие неравенства для модулей этих векторов:

½ + ½ £ ½ ½ + ½½ и ½ + ½³ ½½ ½ — ½½½ причем равенство ½ + ½=½½ ½ — ½½½ достигается только в случае противоположно направленных векторов и .

Эти неравенства вытекают из неравенства треугольника для любых точек А, В и С ( в том числе и лежащих на одной прямой).

Анимация двух векторов.

4. Сложение векторов

При сложении векторов, как и при сложении чисел, выполняются переместительный и сочетательный законы. Кроме этого вы познакомитесь с правилом, по которому можно построить сумму двух неколлинеарных векторов.

5. Переместительный закон сложения.

Теорема: (Переместительный закон сложения векторов или коммутативность сложения)

Для любых векторов и справедливо равенство: + = +

Доказательство: Рассмотрим сначала случай коллинеарных векторов и . Тогда либо , либо . Если , то отложим на прямой а от произвольной точки А вектор = , а затем от точки В отложим вектор = . Тогда по определению = + . Теперь на прямой b½½ а от произвольной точки А1 отложим вектор =, затем =. Тогда по определению = +. , т. к. ½½ = ½ + ½ = ½ ½ + ½½ и ½½ = ½ +½ = ½½ +½½. ½ ½ и½½ — скаляры, то

½ ½ + ½½=½½ +½½, поэтому ½½=½½.

Если , то отложим на прямой а от произвольной точки А вектор = , а затем от точки В отложим вектор = . Тогда по определению = + . Теперь на прямой b½½ а от произвольной точки А1 отложим вектор =, затем =. Тогда по определению = +. , т. к. ½½ = ½ + ½ =½ ½ ½ -½½½ и ½½ = ½ +½ = ½ ½½ -½ ½½. ½ ½ и½½ — скаляры, то

½ ½ ½ -½½ ½=½ ½½ -½ ½½, поэтому ½½=½½.

6. Правило параллелограмма

Раньше, чтобы получить сумму векторов и , мы пользовались правилом треугольника. В доказательстве предыдущей теоремы мы получили правило параллелограмма: Если два вектора не коллинеарны, то их сумма представляется диагональю построенного на них параллелограмма. Итак, чтобы сложить неколлинеарные векторы и , нужно отложить от произвольной точки О вектор = и = и построить параллелограмм ОАСВ. Тогда = +

Тренажер

Укажи вектор, равный сумме двух векторов

7.Сочетательный закон умножения

Операция сложения векторов, как и операция сложения чисел, обладает и сочетательным свойством.

Теорема: (Сочетательный закон сложения, или ассоциативность сложения).Для любых , и справедливо равенство: ( + )+ = + (+)

Доказательство: Отложим от точки А вектор = , а затем от точки В — вектор = и от точки С — вектор=. Т. к. по правилу треугольника + =+=

И + =+=, то ( + )+ = (+)+=+ =

И + (+) = +(+)=+=. Итак, ( + )+ = + (+)

Замечание: Сочетательный закон сложения векторов справедлив для любого числа векторов

Тренажер (отрабатываются навыки законов сложения)

Укажите недостающие значения в формулах.

8. Сумма нескольких векторов

Суммой нескольких векторов называется вектор, получающийся после ряда последовательных сложений: к первому вектору прибавляется второй, к полученному вектору прибавляется третий и т. д. Сумма векторов , , и обозначается так: ++ +. Из определения вытекает способ построения суммы нескольких векторов.

Построим, например, сумму ++ + векторов , , и. От произвольной точки О отложим вектор =, от точки А отложим вектор =, а затем от точки В — вектор =, наконец, от точки С — вектор =. Тогда, по определению, вектор — сумма векторов , , и или = ++ +.

Тренажер (показ анимации сложения пяти и семи векторов)

1. Два вектора, имеющие равные модули и противоположно направленные, называются противоположными.

2. Суммой двух векторов называется вектор, построенный по правилу треугольника.

3. Правилом треугольника называется следующее последовательное построение: сначала откладывают от произвольной точки А вектор =, а потом от точки В — вектор =. Тогда = +

4. Если вектор складывается с противоположным ему вектором, то в сумме получится нулевой вектор.

5. Теорема (Переместительный закон сложения): Для любых векторов и справедливо равенство: +=+

6. Правило параллелограмма: если два вектора не коллинеарны, то их сумма представляется диагональю построенного параллелограмма.

7. Теорема(Сочетательный закон сложения): Для любых векторов и справедливо равенство: ( +)+ = +(+ ).

8. Суммой нескольких векторов называется вектор, получающийся после ряда последовательных сложений: к первому вектору прибавляется второй, к полученному вектору прибавляется третий.

9. Способ построения суммы нескольких векторов называется правилом многоугольника.

10. Если начало первого вектора совпадает с концом последнего, то суммой таких векторов будет нулевой вектор.

IV. Закрепление полученных знаний:

1. Дан треугольник АВС. Выразите через векторы = и = вектор

А) —

Б) —

В) +

2. Векторы и отложены от точек А и А1, причем = =, ==. Как называется фигура АСС1А1?

а) =—

б) = —

в) =+

А) Вектор

Б) Вектор

В) Вектор

V. Подведение итогов.

VI. Задание на дом: п.79-81, №№ 000, 761, 762 (а, в,г, д)

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Урок «Сложение и вычитание векторов»

Краткое описание документа:

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

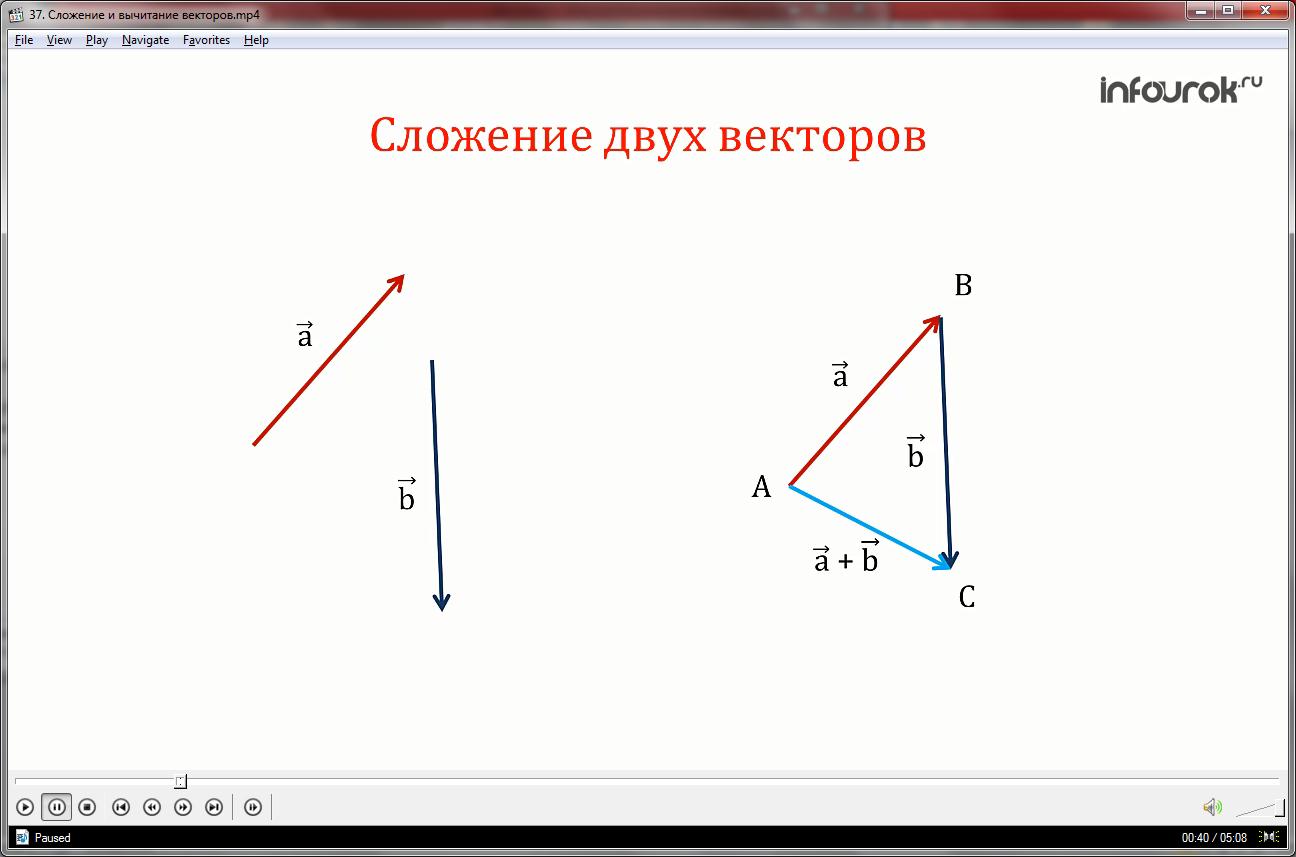
Введем правило сложения двух векторов.

Пусть нам даны два неколлинеарных вектора a и b. Отложим от произвольной точки пространства А вектор АВ, равный вектору а. Затем от точки В отложим вектор ВС, равный вектору b. Вектор АС называется суммой векторов а и b.

Нужно отметить, что сумма векторов не зависит от выбора точки А.

Это правило сложения векторов называется правилом треугольника.

Правило треугольника: для любых трёх точек А, В, С имеет место равенство: вектор АВ плюс вектор ВС получается вектор АС.

При сложении неколлинеарных векторов можно воспользоваться правилом параллелограмма.

Пусть даны векторы а и b. От произвольной точки А отложим векторы АВ и АС, равные соответственно а и b. Достроим до параллелограмма, проведя дополнительные линии, параллельно данным векторам. Вектор AD являющийся диагональю параллелограмма, выходящий из точки А есть сумма векторов а и b.

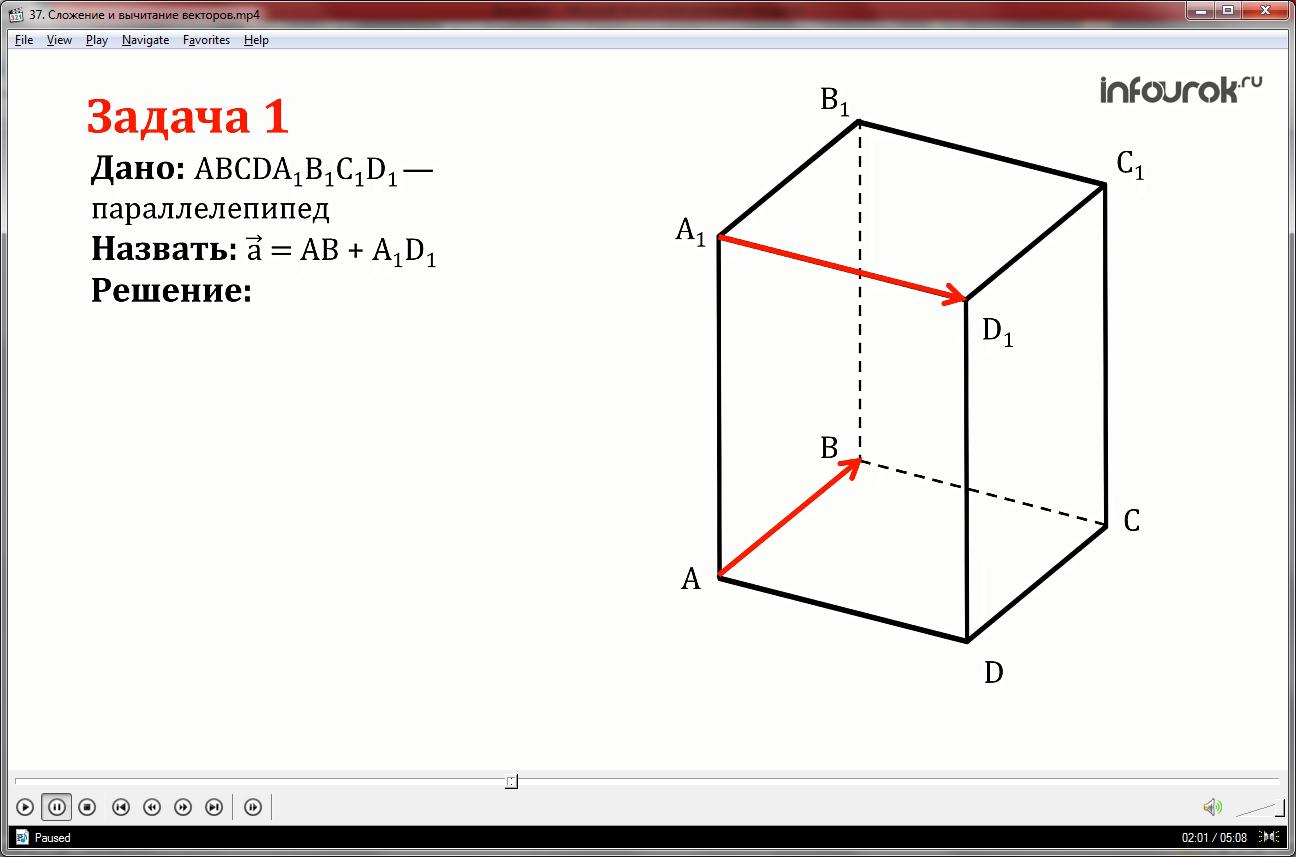
Решим задачу №327 под буквой а.

На рисунке изображен параллелепипед ABCDA1B1C1D1.Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов AB и A1D1 .

Воспользуемся правилом параллелограмма. К вектору АВ прибавим вектор АD, равный вектору A1D1.

Суммой этих векторов будет диагональ основания параллелепипеда, то есть вектор АС.

Напомним свойства сложения векторов, так как они ни чем не отличаются от свойств сложения векторов в планиметрии:

Для любых трех векторов а, бэ и це, выполняются равенства

1) переместительный закон

2) сочетательный закон

Введем определение противоположных векторов.

Два вектора называются противоположными, если их длины равны и они противоположно направлены

Вектор минус а противоположен вектору а

Вектор DF противоположен вектору FD, и равен минус вектор FD

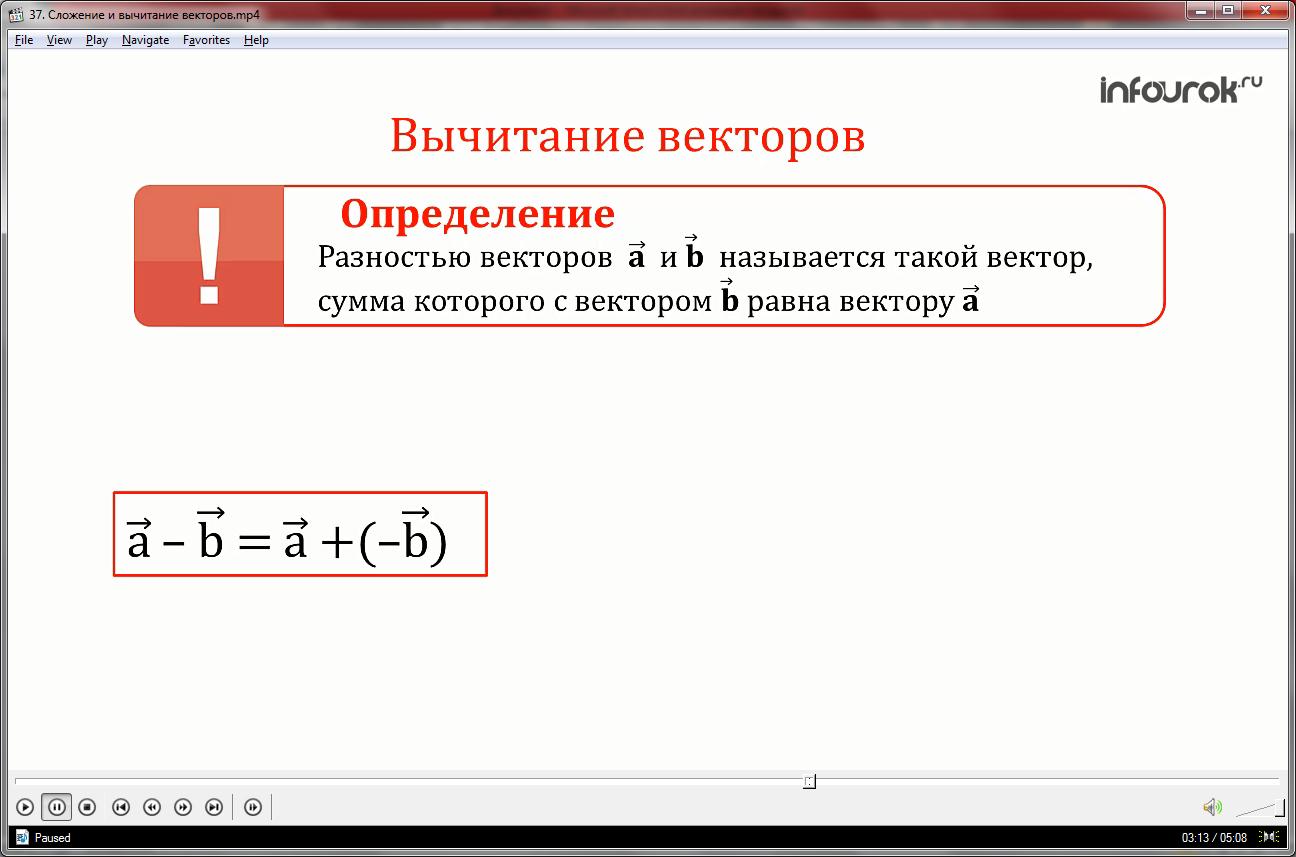
Определим вычитание векторов

Разностью векторов и называется такой вектор, сумма которого с вектором равна вектору .

Разность векторов и можно найти как сумму вектора с противоположным вектором вектору .

Введем правило вычитания векторов.

Пусть нам даны два неколлинеарных вектора и . Отметим произвольную точку А. Отложим от точки А вектор АВ , равный вектору а и вектор АС, равный вектору b. Вектор СВ будет разностью данных векторов.

Существует правило для трех точек.

Любой вектор можно представить как разность двух векторов, проведенных из одной точки.

Добавляем третью точку (любую) и задаем разность из вектора, проведенного из этой точки в конец данного вектора минус вектор, проведенный в начало.

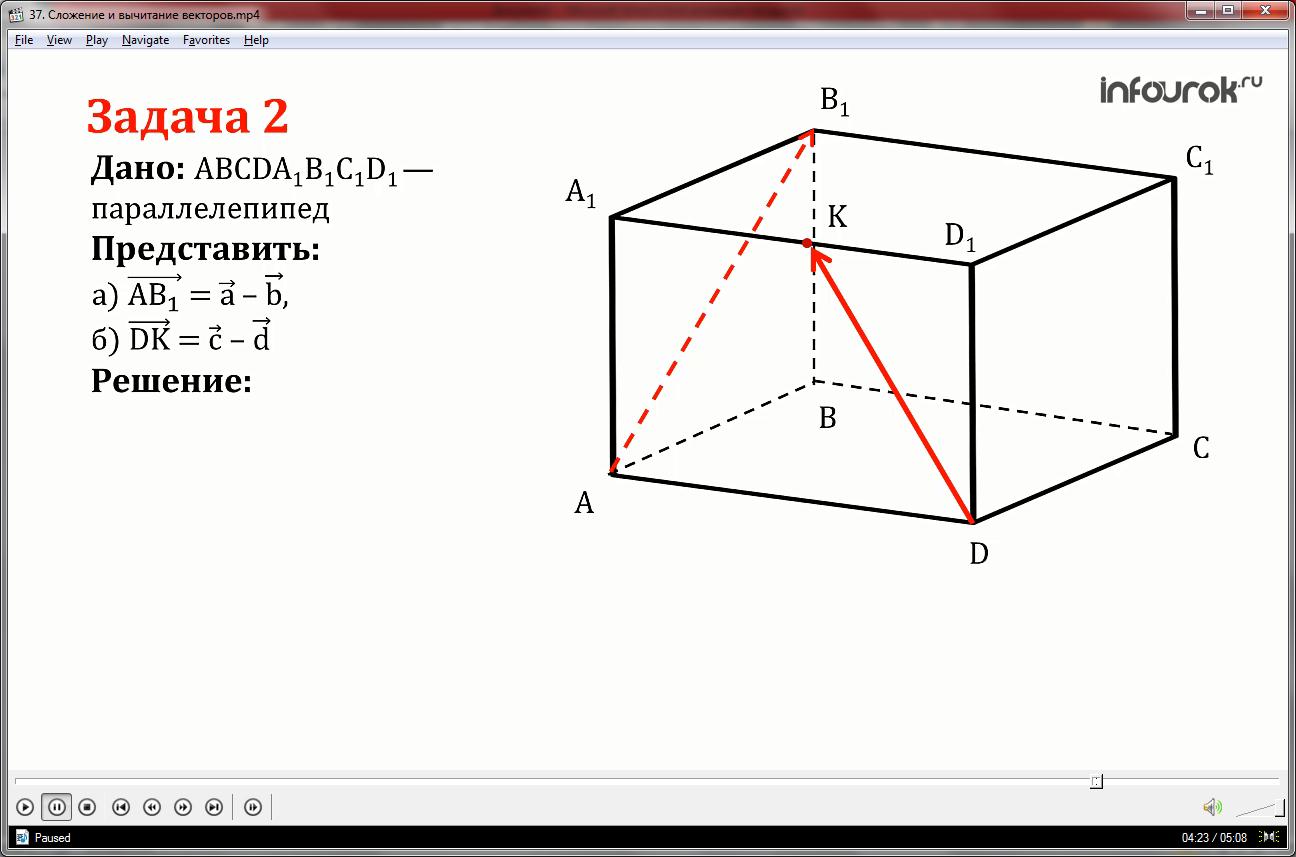
Решим задачу №332

На рисунке изображен параллелепипед ABCDA1B1C1D1 Представьте векторы АВ1 и DK в виде разности двух векторов, начала и концы которых совпадают с отмеченными на рисунке точками.

Рассмотрим вектор АВ1 и воспользуемся правилом трех точек. Третьей точкой удобно взять точку А1. Вектор, проведенный в конец то есть в точку В1 будет А1В1 и в начало точку А – вектор А1А. Получаем АВ1 равно А1В1 минус А1А.

Выполним это же задание для вектора DK. Здесь третьей точкой удобно взять точку D1. Вектор в конец ¬ — D1K, в начало — D1D. Получим вектор DK равен D1K минус D1D.