Каждая сторона треугольника равна сумме

Определение

Существующие треугольники — это такие треугольники,
существование которых можно доказать с помощью неравенств.

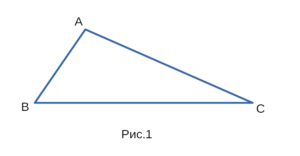
Например существование треугольника, изображенного на рисунке 1,
можно доказать с помощью неравенств: AB + BC > AC, AC + BC > AB, AB + AC > BC
Если эти три неравенства истинны значит треугольник существует,
иначе он не существует.

Также существование того или иного треугольника можно проверить с
помощью одного условия: Если большая сторона треугольника меньше
суммы двух других сторон, значит треугольник существует,
иначе он не существует.

Теорема

Для доказательства того, о чем мы говорили существует теорема под названием неравенство треугольника. Формулировка теоремы:
каждая сторона треугольника меньше суммы двух других сторон.

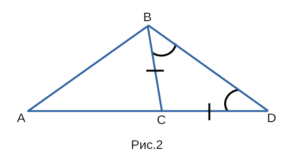
Докажем, что каждая сторона треугольника, изображенного на рисунке 2, меньше суммы двух других сторон:

Доказательство теоремы

1. Проведем отрезок CD равный отрезку CB.
2. △BCD — равнобедренный, значит ∠ CBD=∠CDB.
3. Рассмотрим △ABD: ∠ ABD >∠ CBD, следовательно ∠ ABD >∠ CDB, то AB

Видео:Неравенство треугольника ★ Любая сторона треугольника меньше суммы двух других сторонСкачать

Каждая сторона треугольника равна сумме

Какие из следующих утверждений верны?

1) В треугольнике ABC, для которого AB = 4, BC = 5, AC = 6, угол A наибольший.

2) Каждая сторона треугольника не превосходит суммы двух других сторон.

3) Если два треугольника подобны, то их соответствующие стороны равны.

4) Площадь многоугольника, описанного около окружности, равна произведению его периметра на радиус вписанной окружности.

Проверим каждое из утверждений.

1) «В треугольнике ABC, для которого AB = 4, BC = 5, AC = 6, угол A наибольший.» — неверно, так как против большего угла лежит большая сторона.

2) «Каждая сторона треугольника меньше суммы двух других сторон.» — верно, каждая сторона меньше суммы двух других сторон.

3) «Если два треугольника подобны, то их соответствующие стороны равны.» — неверно, если треугольники подобны их соответствующие стороны пропорциональны.

4) «Площадь многоугольника, описанного около окружности, равна произведению его периметра на радиус вписанной окружности.» — неверно, площадь многоугольника равна половине произведения периметра на радиус вписанной окружности.

Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Треугольник.

Треугольником называется геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки, образующие треугольник, называются сторонами треугольника, а их общие концы — вершинами треугольника.

Признаки равенства треугольников

1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Признаки подобия треугольников

1. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Соотношения между сторонами и углами треугольника

1. Каждая сторона треугольника меньше суммы двух других сторон.
2. Сумма углов треугольника равна 180°.
3. Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
4. Напротив большей стороны треугольника лежит больший угол, а напротив большего угла большая сторона.
5. Напротив меньшей стороны треугольника лежит меньший угол, а напротив меньшего угла меньшая сторона.
6. Отношения сторон к синусу противоположных углов постоянно и равняется диаметру описанной окружности (теорема синусов).
7. Квадрат длины стороны треугольника равен сумме квадратов длин других сторон минус удвоенное произведение длин этих сторон на косинус угла между ними (теорема косинусов).
8. Разность двух сторон треугольника относится к их сумме, как тангенс полуразности противолежащих углов к тангенсу полусуммы этих углов (теорема тангенсов).

Площадь треугольника

Площадь треугольника через сторону и высоту, проведенную к этой стороне:

Площадь треугольника через радиус вписанной окружности и полупериметр :

Площадь треугольника через радиус вневписанной окружности и полупериметр:

Площадь треугольника через радиусы вневписанных окружностей и радиус вписанной окружности:

Площадь треугольника через радиус описанной окружности и стороны:

Площадь треугольника через две стороны и угол между ними:

Площадь треугольника через высоту и сторону:

Площадь треугольника через длины сторон и полупериметр (формула Герона):

Интересная теорема об отношении площадей треугольников, имеющих равный угол:

Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

Замечательные точки треугольника

Инцентр треугольника — точка пересечения биссектрис треугольника. Инцентр является центром вписанной окружности.

Центроид треугольника — точка пересечения медиан треугольника.

Ортоцентр треугольник — точка пересечения прямых, содержащих высоты треугольника.

Про другие замечательные точки и прямые треугольника вы можете прочитать здесь.

🎬 Видео

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Почему каждая сторона треугольника меньше суммы двух других сторон?Скачать

Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать

Неравенство треугольника. Геометрия 7 класс. Доказательство. Задачи по рисункам.Скачать

Чему равна сумма углов выпуклого многоугольникаСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Геометрия 7 класс (Урок№24 - Соотношения между сторонами и углами треугольника. Неравенство треуг.)Скачать

Внешний угол треугольникаСкачать

Лайфхак для школьников\Теорема: каждая сторона треугольника меньше суммы двух других сторонСкачать

Неравенства треугольника. Практическая часть. 7 класс.Скачать

№251. Докажите, что каждая сторона треугольника больше разности двух других сторон.Скачать

7 класс, 34 урок, Неравенство треугольникаСкачать

Внешний угол треугольника равен сумме его ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

№1082. Чему равна сумма внешних углов правильного n-угольника, если при каждой вершинеСкачать

Периметр треугольника. Как найти периметр треугольника?Скачать

Задача про соотношение сторон. Геометрия 7 класс.Скачать

Геометрия 7 класс (Урок№28 - Обобщение по теме «Соотношение между сторонами и углами треугольника».)Скачать

✓ Старая вирусная задача | Не баян, а классика | Ботай со мной #085 | Борис ТрушинСкачать