Сумма противоположных углов в четырехугольнике не превосходит 180

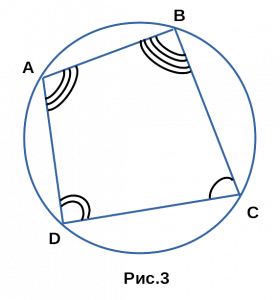
Какие из следующих утверждений верны?

1) Если противоположные углы выпуклого четырехугольника попарно равны, то этот четырехугольник — параллелограмм.

2) Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°.

3) Сумма двух противоположных углов четырехугольника не превосходит 180°.

4) Если основания трапеции равны 4 и 6, то средняя линия этой трапеции равна 10.

Проверим каждое из утверждений.

1) «Если противоположные углы выпуклого четырехугольника попарно равны, то этот четырехугольник — параллелограмм.» — верно, по признаку параллелограмма.

2) «Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°.» — верно, Сумма углов выпуклого четырёхугольника равна 360°.

3) «Сумма двух противоположных углов четырехугольника не превосходит 180°.» — неверно, сумма противоположных углов четырехугольника может быть больше 180°.

4) «Если основания трапеции равны 4 и 6, то средняя линия этой трапеции равна 10.» — неверно, средняя линия трапеции равна полусумме оснований.

Видео:Геометрия Если в четырехугольнике сумма противолежащих углов равна 180, то около него можно описатьСкачать

Сумма углов четырехугольника

Свойства

1. Сумма углов четырехугольника равна 360°.
   ∠A + ∠B + ∠C + ∠D = 360°.
   
2. Если четырехугольник правильный, то каждый угол по 90°
   и этот четырехугольник является квадратом.
   ∠A = ∠B = ∠C = ∠D, ⇒ ∠A = ∠B = ∠C = ∠D = 90°,
   ABCD — квадрат.
   
3. Сумма противоположных углов четырехугольника равна 180°,
   если около четырехугольника описана окружность.
   ∠A + ∠С = ∠В + ∠D = 180°.
   

Такие четырехугольники называют вписанными.

Это все виды четырехугольников,
которые изучаются в школьном
курсе по геометрии.

Видео:Уроки геометрии. Чему равна сумма углов четырехугольника?Скачать

Четырёхугольник

Сегодня рассмотрим геометрическую фигуру — четырехугольник. Из названия этой фигуры уже становится понятно, что у этой фигуры есть четыре угла. А вот остальные характеристики и свойства этой фигуры мы рассмотрим ниже.

Видео:Сумма углов четырехугольника | Математика 8 класс | Четырехугольник | Геометрия 8 классСкачать

Что такое четырех угольник

Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки. Площадь четырехугольника равна полупроизведению его диагоналей и угла между ними.

Четырехугольник — это многоугольник с четырьмя вершинами, три из которых не лежат на одной прямой.

Четырехугольник — это геометрическая фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, последовательно соединенная отрезками.

Видео:ПОЧЕМУ СУММА УГЛОВ В ТРЕУГОЛЬНИКЕ РАВНА 180? #shorts #геометрия #егэ #огэ #треугольникСкачать

Виды четырехугольников

• Четырехугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
• Четырехугольник, у которого две противоположные стороны параллельны, а две другие − нет, называется трапецией.
• Четырехугольник, у которого все углы прямые, является прямоугольником.
• Четырехугольник, у которого все стороны равны, является ромбом.
• Четырехугольник, у которого все стороны равны и все углы прямые, называется квадратом.

Четырехугольник может быть:

Самопересекающийся четырехугольник — это четырехугольник, у которого любые из его сторон имеют точку пересечения (на рисунке синим цветом).

Невыпуклый четырехугольник — это четырехугольник, в котором один из внутренних углов более 180 градусов (на рисунке обозначен оранжевым цветом).

Сумма углов любого четырехугольника, который не является самоперсекающимся всегда равна 360 градусов.

Видео:Суммы противоположных углов четырехугольника, вписанного в окружность, равны 180 градусов #репетиторСкачать

Особые виды четырехугольников

Четырехугольники могут обладать дополнительными свойствами, образуя особые виды геометрических фигур:

• Параллелограмм
• Ромб
• Прямоугольник
• Квадрат
• Трапеция
• Дельтоид
• Контрпараллелограмм

Видео:Чему равна сумма углов выпуклого многоугольникаСкачать

Четырехугольник и окружность

Четырехугольник, описанный вокруг окружности (окружность, вписанная в четырехугольник).

Главное свойство описанного четырехугольника:

Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин противоположных сторон равны.

Четырехугольник, вписанный в окружность (окружность, описанная вокруг четырехугольника)

Главное свойство вписанного четырехугольника:

Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы противоположных углов равны 180 градусов.

Видео:Сумма противоположных углов впмсанного четырёхугольникаСкачать

Свойства длин сторон четырехугольника

Модуль разности любых двух сторон четырёхугольника не превосходит суммы двух других его сторон.

Важно. Неравенство верно для любой комбинации сторон четырехугольника. Рисунок приведен исключительно для облегчения восприятия.

В любом четырёхугольнике сумма длин трёх его сторон не меньше длины четвёртой стороны.

Важно. При решении задач в пределах школьной программы можно использовать строгое неравенство (

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

📸 Видео

3 правила для вписанного четырехугольника #shortsСкачать

Задание 24 Сумма углов четырехугольникаСкачать

Описанный четырехугольник, сумма противоположных сторонСкачать

Вписанный в окружность четырёхугольник.Скачать

11 класс, 43 урок, Вписанный четырехугольникСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

8 класс, 3 урок, ЧетырехугольникСкачать

5 Описанная окружность около четырехугольника. СвойствоСкачать

Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать

Геометрия Если в выпуклом четырехугольнике суммы противолежащих сторон равны, то в него можноСкачать

Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Сумма углов вписанного четырехугольникаСкачать