Сумма и разность векторов параллелепипеда

Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .

Существование: Имеем два следующих случая:

Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .

Из данного выше построения сразу же будет следовать единственность данного вектора.

Видео:10 класс, 44 урок, Правило параллелепипедаСкачать

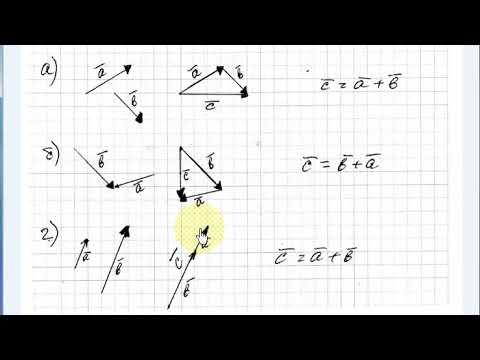
Сумма векторов. Сложение векторов. Правило треугольника

Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.

Суммой нескольких векторов ( vec ) , ( vec ) , ( vec,;ldots ) называется вектор ( vec ) , получающийся в результате последовательного сложения данных векторов.

Такая операция выполняется по правилу многоугольника.

Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( <+ , + , + > right) )

Отметим несколько свойств сложения двух векторов:

Для произвольного вектора ( overrightarrow ) выполняется равенство

Для произвольных точек ( A, B и C ) справедливо следующее равенство

Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.

Видео:Сложение векторов. Правило параллелограмма. 9 класс.Скачать

Разность векторов. Вычитание векторов

Разность двух одинаковых векторов равна нулевому вектору :
( vec — vec = vec )

Длина нулевого вектора равна нулю:
( left| vec right| = 0 )

Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec — vec = left( <- , — , — > right) )

Видео:Правило параллелепипеда для векторовСкачать

Умножение вектора на число

Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .

Определение Произведением вектора ( overrightarrow ) на действительное число ( k ) называется вектор ( overrightarrow ) удовлетворяющий следующим условиям:

Длина вектора ( overrightarrow ) равна ( left|overrightarrowright|=left|kright||overrightarrow| ) ;

Векторы ( overrightarrow ) и ( overrightarrow ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )

Обозначение: ( overrightarrow=koverrightarrow ) .

Видео:Вычитание векторов. 9 класс.Скачать

Правило параллелепипеда. Разложение вектора

Вы будете перенаправлены на Автор24

Видео:Сложение векторов. 9 класс.Скачать

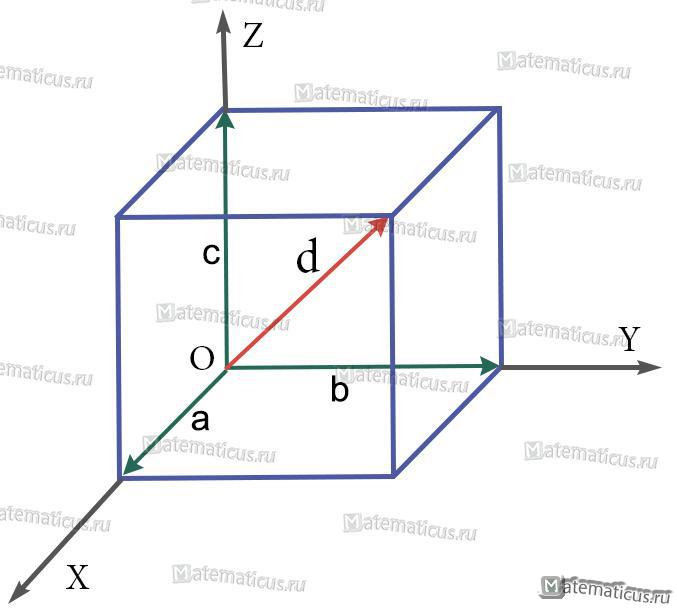
Правило параллелепипеда

Для правила сложения трех векторов рассмотрим следующую задачу.

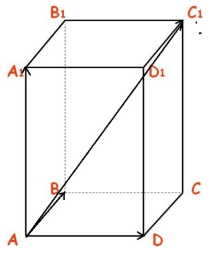
Дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Доказать, что $overrightarrow+overrightarrow+overrightarrow=overrightarrow$

Доказательство.

Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:

Так как $overrightarrow=overrightarrow, overrightarrow=overrightarrow$

Из этой задачи получаем следующее правило для нахождения сложения трех векторов. Чтобы найти сумму трех векторов $overrightarrow,overrightarrow и overrightarrow$ нужно от произвольной точки $O$ отложить векторы $overrightarrow=overrightarrow$, $overrightarrow=overrightarrow$ и $overrightarrow=overrightarrow$ и построим параллелепипед на этих векторах. Тогда вектор диагонали $overrightarrow$ и будет суммой этих трех векторов. Это правило называется правилом параллелепипеда для сложения трех векторов.

Видео:44. Правило параллелепипедаСкачать

Разложение вектора по двум неколлинеарным векторам

Вспомним сначала, какие векторы называются компланарными.

Два вектора, которые параллельны одной плоскости называются компланарными.

Произвольный вектор $overrightarrow

$ можно разложить по трем некомпланарным векторам $overrightarrow, overrightarrow$ и $overrightarrow$ с единственными коэффициентами разложения.

Математически это можно записать следующим образом

Доказательство.

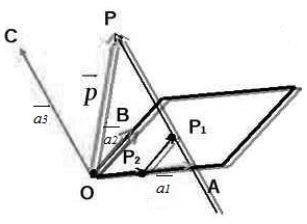
Существование: Пусть нам даны три некомпланарных вектора $overrightarrow, overrightarrow$ и $overrightarrow$. Выберем произвольную точку $O$ и построим следующие векторы:

[overrightarrow=overrightarrow, overrightarrow=overrightarrow, overrightarrow=overrightarrow и overrightarrow

=overrightarrow]

Рассмотрим следующий рисунок:

Произведем следующие дополнительные построения. Проведем через точку $P$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает плоскость $OAB$ в точке $P_1$. Далее, проведем через точку $P_1$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает прямую $OA$ в точке $P_2$ (смотри рисунок выше).

Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:

Так как векторы $overrightarrow$ и $overrightarrow$ коллинеарны, то

Так как векторы $overrightarrow

$ и $overrightarrow$ коллинеарны, то

Так как векторы $overrightarrow

$ и $overrightarrow$ коллинеарны, то

Тогда, получаем, что

Существование разложения доказано.

Единственность: Предположим противное. Пусть существует еще одно разложение вектора $overrightarrow

$ по векторам $overrightarrow, overrightarrow$ и $overrightarrow$:

Вычтем эти разложения друг из друга

Из этого получаем

Теорема доказана.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Сложение и вычитание векторов

Видео:Сложение и вычитание векторов. Практическая часть. 11 класс.Скачать

Сложение векторов по правилу параллелограмма

Правило параллелограмма

Если слагаемые a и b не коллинеарны, то

c=a+b

Видео:8 класс, 43 урок, Сумма двух векторовСкачать

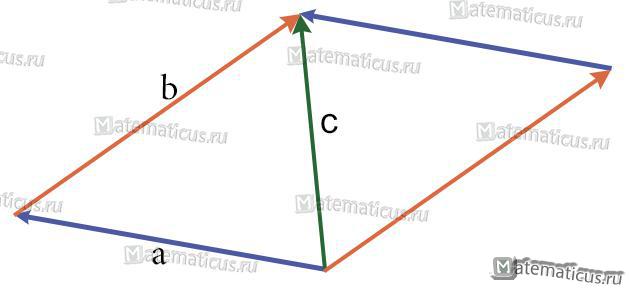
Сложение векторов по правилу треугольника

Правило треугольника

Суммой векторов a (на рисунке зелёный вектор ) и b (на рисунке синий вектор ) называется третий вектор c (на рисунке красный вектор ) , получаемый следующее построение:

Нельзя смешивать понятие «сумма отрезков» с понятием «сумма векторов».

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Правило параллелепипеда

Если три вектора a, b, c после приведения к общему началу не лежат в одной плоскости , то их сумма равна диагонали параллелепипеда

d=a+b+c

Видео:10 класс, 40 урок, Сложение и вычитание векторовСкачать

Сложение противоположных векторов

Сумма противоположных векторов равна нуль-вектору, т.е.

a+(-a)=0

Видео:Сумма и разность векторов. Урок 2. Геометрия 9 классСкачать

Свойство переместительности ( переместительный закон )

От перестановки слагаемых сумма векторов не меняется.

с=a+b= b+a

Видео:8 класс, 44 урок, Законы сложения векторов. Правило параллелограммаСкачать

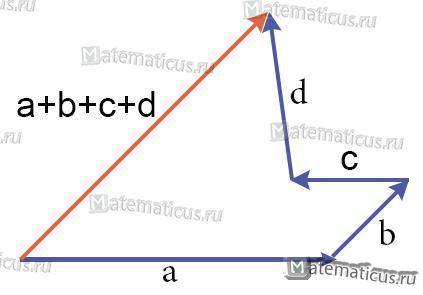
Сочетательное свойство ( сочетательный закон )

Слагаемые векторы можно группировать как угодно.

a+(b+c+d) = a+b+c+d

Видео:СУММА ВЕКТОРОВ правило треугольникаСкачать

Вычитание векторов

Вычесть вектор а (вычитаемое) из вектора b (уменьшаемое) значит найти новый вектор x (разность), который в сумме с вектором а даёт вектор b.
Разность векторов обозначается: a-b
Вычитание есть действие обратное сложению (сложение векторов).
Вычитание векторов показаны на рисунках ниже:

Примечание
Модуль разности может быть меньше модуля «уменьшаемого», но может быть и больше или равен ему. Эти случаи показаны на рисунке выше.

🎬 Видео

Сложение и вычитание векторовСкачать

сложение ВЕКТОРОВ вычитание ВЕКТОРОВ 9 класс геометрия АтанасянСкачать

1. Векторы и параллелограмм задачи №1Скачать

Урок 4. Векторы. Сложение векторов. Правило треугольника. Правило параллелограмма.Скачать

10 класс, 41 урок, Сумма нескольких векторовСкачать

Геометрия 9 класс (Урок№2 - Сумма двух векторов. Законы сложения векторов.)Скачать