Сумма двух смежных углов в четырехугольнике

Свойства

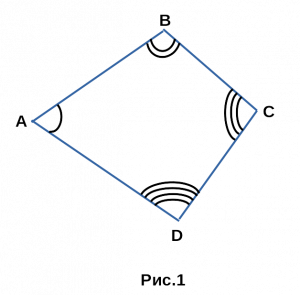
1. Сумма углов четырехугольника равна 360°.
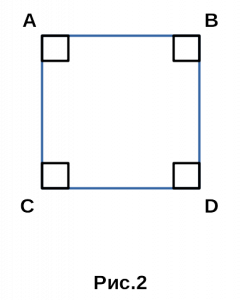
   ∠A + ∠B + ∠C + ∠D = 360°.
   
2. Если четырехугольник правильный, то каждый угол по 90°
   и этот четырехугольник является квадратом.
   ∠A = ∠B = ∠C = ∠D, ⇒ ∠A = ∠B = ∠C = ∠D = 90°,
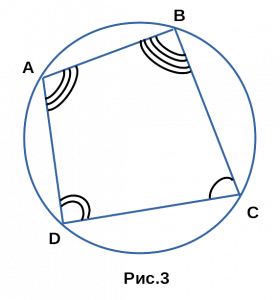
   ABCD — квадрат.
   
3. Сумма противоположных углов четырехугольника равна 180°,
   если около четырехугольника описана окружность.
   ∠A + ∠С = ∠В + ∠D = 180°.
   

Такие четырехугольники называют вписанными.

Это все виды четырехугольников,
которые изучаются в школьном
курсе по геометрии.

Видео:Уроки геометрии. Чему равна сумма углов четырехугольника?Скачать

Все, что нужно знать о свойствах четырехугольников

В этой статье мы рассмотрим все основные свойства и признаки четырехугольников.

Для начала я расположу все виды четырехугольников в виде такой сводной схемы:

Схема замечательна тем, что четырехугольники, стоящие в каждой строке обладают ВСЕМИ СВОЙСТВАМИ ЧЕТЫРЕХУГОЛЬНИКОВ, РАСПОЛОЖЕННЫХ НАД НИМИ. Поэтому запоминать надо совсем немного.

Трапеция — это четырехугольник, две стороны которого параллельны, а две другие не параллельны. Параллельные стороны называются основаниями трапеции, а не параллельные — боковыми сторонами.

1. В трапеции сумма углов, прилежащих к боковой стороне равна 180°: А+В=180°, C+D=180°

2. Биссектриса любого угла трапеции отсекает на ее основании отрезок, равный боковой стороне:

3. Биссектрисы смежных углов трапеции пересекаются под прямым углом.

4.Трапеция называется равнобедренной, если ее боковые стороны равны:

В равнобедренной трапеции

• углы при основании равны,
• проекции боковых сторон на основание равны: .

5. Площадь трапеции равна произведению полусуммы оснований на высоту:

Параллелограм — это четырехугольник, у которого противоположные стороны попарно параллельны: В параллелограмме:

• противоположные стороны и противоположные углы равны
• диагонали параллелограмма делятся точкой пересечения пополам:

Соответственно, если четырехугольник обладает этими свойствами, то он является параллелограммом.

Площадь параллелограмма равна произведению основания на высоту:

или произведению сторон на синус угла между ними:

:

Ромб — это параллелограмм, у которого все стороны равны:

• противоположные углы равны
• диагонали точкой пересечения делятся пополам
• диагонали взаимно перпендикулярны
• диагонали ромба являются биссектрисами углов

Площадь ромба равна половине произведения диагоналей:

или произведению квадрата стороны на синус угла между сторонами:

Прямоугольник — это параллелограмм, у которого все углы прямые:

• Диагонали прямоугольника равны.
• Диагонали точкой пересечения делятся пополам.

Площадь прямоугольника равна произведению его сторон:

.

Квадрат — это прямоугольник, у которого все стороны равны

Квадрат — это ромб, у которого все углы прямые.

Соответственно: квадрат обладает свойствами ромба и прямоугольника:

• все углы равны 90 градусов
• диагонали точкой пересечения делятся пополам
• диагонали взаимно перпендикулярны
• диагонали являются биссектрисами углов
• диагонали равны

Площадь квадрата равна квадрату его стороны.

Площадь квадрата равна половине произведения диагоналей.

И.В. Фельдман, репетитор по математике.

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Четырехугольник

Видео:7 класс, 11 урок, Смежные и вертикальные углыСкачать

Определение четырехугольника

Определение 1. Четырехугольник − это замкнутая ломаная линия, состоящая из четырех звеньев.

Определение 2. Четырехугольник − геометрическая фигура (многоугольник), состоящая из четырех точек, никакие три из которых не лежат на одной прямой и последовательно соединенные четырьмя отрезками, называемыми сторонами четырехугольника.

Объединение четырехугольника и ограниченной им части плоскости также называют четырехугольником.

Любой четырехугольник разделяет плоскость на две части, одна из которых называется внутренней областью четырехугольника, а другая внешней областью четырехугольника.

Видео:Сумма двух углов равнобедренной трапеции равна 50° ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

Виды четырехугольников

Четырехугольники бывают следующих видов:

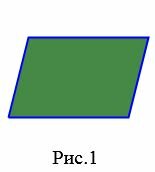
• Параллелограмм − четырехугольник, у которого противоположные стороны попарно вправны и параллельны (Рис.1).
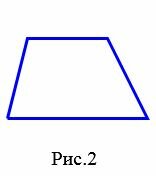
• Трапеция − четырехугольник, у которого две противоположные стороны параллельны (Рис.2).
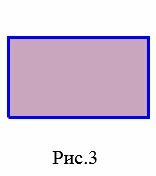
• Прямоугольник − четырехугольник, у которого все углы прямые (Рис.3).
• Ромб − четырехугольник, у которого все стороны равны (Рис.4).
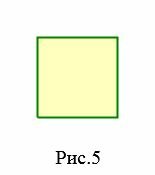
• Квадрат − четырехугольник, у которого все стороны равны и все углы прямые (Рис.5).
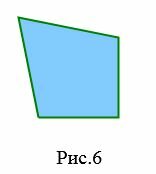
• Дельтоид − четырехугольник, у которого есть две пары равных смежных сторон (Рис.6, Рис.6.1).
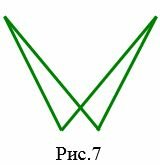
• Антипараллелограмм (или контрпараллелограмм)− четырехугольник, у которого противоположные стороны равны но не параллельны (с самопересечением) (Рис.7).

Видео:Геометрия № 83 №211 Задача найти угол между биссектрисами смежных и односторонних угловСкачать

Обозначение четырехугольника

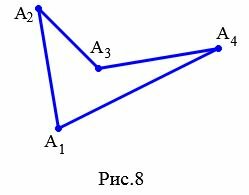
Обозначают четырехугольник буквами, стоящих при его вершинах. Называют четырехугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, четырехугольник на рисунке 8 называют ( small A_1A_2A_3A_4 ) или ( small A_4A_3A_2A_1 ) (Рис.8).

Видео:№429. Докажите, что выпуклый четырехугольник является параллелограммом, если сумма углов, прилежащихСкачать

Соседние вершины четырехугольника

Вершины четырехугольника называются соседними, если они являются концами одной из его сторон.

На рисунке 8 вершины ( small A_2 ) и ( small A_3 ) являются соседними, так как они являются концами стороны ( small A_2A_3. )

Видео:Чему равна сумма углов выпуклого многоугольникаСкачать

Смежные стороны четырехугольника

Стороны четырехугольника называются смежными, если они имеют общую вершину.

На рисунке 8 стороны ( small A_2A_3 ) и ( small A_3A_4 ) являются смежными, так как они имеют общую вершину ( small A_3. )

Видео:№698. Сумма двух противоположных сторон описанного четырехугольника равна 12 см, а радиусСкачать

Простой четырехугольник. Самопересекающийся четырехугольник

Четырехугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).

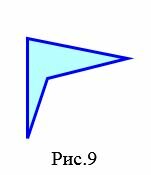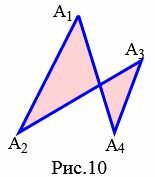На рисунках 9 и 9.1 изображены простые четырехугольники так как стороны четырехугольников не имеют самопересечений. А на рисунке 10 четырехугольник не является простым, так как стороны ( small A_1A_4 ) и ( small A_2A_3 ) пересекаются. Такой четырехугольник называется самопересекающийся.

Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Выпуклый четырехугольник

Четырехугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.

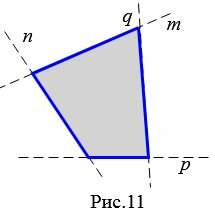На рисунке 11 четырехугольник лежит по одну сторону от прямых ( small m, n, p, q, ) проходящих через стороны четырехугольника. Поэтому такой четырехугольник выпуклый.

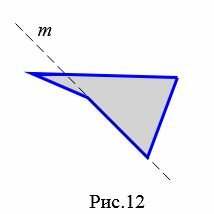На рисунке 12 прямая ( small m) делит четырехугольник на две части, т.е. четырехугольник не лежит по одну сторону от прямой ( small m). Следовательно, этот четырехугольник не является выпуклым.

Видео:Внешний угол треугольникаСкачать

Правильный четырехугольник

Простой четырехугольник называется правильным, если все его стороны равны и все углы равны. Квадрат является правильным четырехугольником, так как все его стороны равны и все его углы равны 90°. Среди четырехугольников других правильных четырехугольников не существует.

На рисунке 5 изображен правильный четырехугольник (квадрат), так как у данного четырехугольника все стороны равны и все углы равны. Четырехугольник (ромб) на на рисунке 4 не является правильным, так как все стороны четырехугольника равны, но все его углы не равны друг другу. Прямоугольник также не является правильным четырехугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Периметр четырехугольника

Сумма всех сторон четырехугольника называется периметром четырехугольника. Для четырехугольника ( small A_1A_2A_3A_4 ) периметр вычисляется из формулы:

Видео:Задание 24 Сумма углов четырехугольникаСкачать

Угол четырехугольника

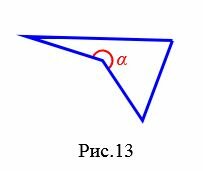
Углом (внутренним углом) четырехугольника при данной вершине называется угол между двумя сторонами четырехугольника, сходящимися к этой вершине. Если четырехугольник выпуклый, то все углы четырехугольника меньше 180°. Если же четырехугольник невыпуклый, то он имеет внутренний угол больше 180° (угол ( small alpha ) на рисунке 13).

Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Внешний угол четырехугольника

Внешним углом четырехугольника при данной вершине называется угол смежный внутреннему углу четырехугольника при данной вершине.

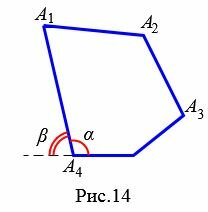На рисунке 14 угол α является внутренним углом четырехугольника при вершине ( small A_4, ) а углы β и γ являются внешними углами четырехугольника при этой же вершине. Очевидно, что при каждой вершине есть два внешних угла.

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Диагональ четырехугольника

Диагоналями называют отрезки, соединяющие две несоседние вершины четырехугольника.

Очевидно, что у четырехугольника две диагонали.

Видео:Угол между биссектрисами смежных угловСкачать

Сумма углов четырехугольника

Для любого простого четырехугольника по крайней мере один диагональ делит его на два треугольника. Сумма углов треугольника равна 180°. Поэтому сумма углов простого четырехугольника равна 360°.

Видео:Сумма двух углов равнобедренной трапеции равна 250° ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

Сумма внешних углов четырехугольника

Пусть задан четырехугольник ( small A_1A_2A_3A_4 .) Внешний угол при вершине ( small A_1) равен ( small 180°-angle A_1.) Аналогично, внешние углы при вершинах ( small A_2, A_3, A_4 ) равны ( small 180°-angle A_2, ) ( small 180°-angle A_3, ) ( small 180°-angle A_4, ) соответственно. Тогда сумма внешних углов четырехугольника равна:

Задача 1. Доказать, что длина любой стороны четырехугольника меньше суммы длин трех его сторон.

Решение. Рассмотрим произвольный четырехугольник ABCD (Рис.15). Покажем, например, что AB

🎥 Видео

Теперь ты будешь находить углы за секунды. Как найти внешний угол треугольника? #математика #углыСкачать

8 класс, 3 урок, ЧетырехугольникСкачать

Задача, которую боятсяСкачать

Геометрия 10 класс (Урок№2 - Четырехугольники.)Скачать