- Теоретическая механика: Центр тяжести
- § 23. Определение положения центра тяжести тела, составленного из тонких однородных стержней
- § 24. Определение положения центра тяжести фигур, составленных из пластинок
- § 25. Определение положения центра тяжести сечений, составленных из профилей стандартного проката
- § 26. Определение положения центра тяжести тела, составленного из частей, имеющих простую геометрическую форму
- Центры тяжести многоугольников и многогранников
- Двумерный случай: многоугольники
- Центр масс системы точек
- Центр масс каркаса
- Центр масс сплошной фигуры
- Случай треугольника
- Случай треугольника: доказательство
- Случай многоугольника
- Случай многоугольника: альтернативный способ
- Трёхмерный случай: многогранники
- Центр масс системы точек
- Центр масс каркаса многогранника
- Центр масс поверхности многогранника
- Центр масс сплошного многогранника
- Случай тетраэдра
- Случай произвольного многогранника
- Презентация «Техническая механика. Центр тяжести»
- Описание презентации по отдельным слайдам:
- Охрана труда
- Библиотечно-библиографические и информационные знания в педагогическом процессе
- Охрана труда
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 🔍 Видео
Теоретическая механика:
Центр тяжести
Смотрите также решения задач по нахождению центра тяжести в онлайн решебниках Яблонского (С.8) и Мещерского (§ 9).
Центр тяжести – точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил (Е. М. Никитин, § 42). Поэтому формулы для определения положения центра тяжести различных тел имеют вид:
xc = (∑ Gixi) / ∑ Gi;
(1) yc = (∑ Giyi) / ∑ Gi;
zc = (∑ Gizi) / ∑ Gi.
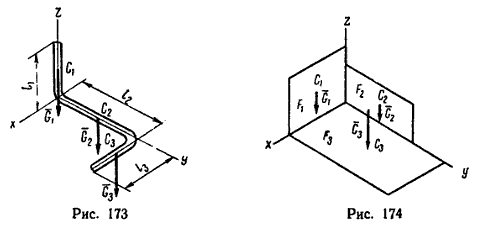
Если тело, центр тяжести которого нужно определить, можно отождествить с фигурой, составленной из линий (например, замкнутый или незамкнутый контур, изготовленный из проволоки, как на рис. 173), то вес Gi каждого отрезка li можно представить в виде произведения
Gi = lid,
где d – постоянный для всей фигуры вес единицы длины материала.
После подстановки в формулы (1) вместо Gi их значений lid постоянный множитель d в каждом слагаемом числителя и знаменателя можно вынести за скобки (за знак суммы) и сократить. Таким образом, формулы для определения координат центра тяжести фигуры, составленной из отрезков линий , примут вид:
xc = (∑ lixi) / ∑ li;
(2) yc = (∑ liyi) / ∑ li;
zc = (∑ lizi) / ∑ li.
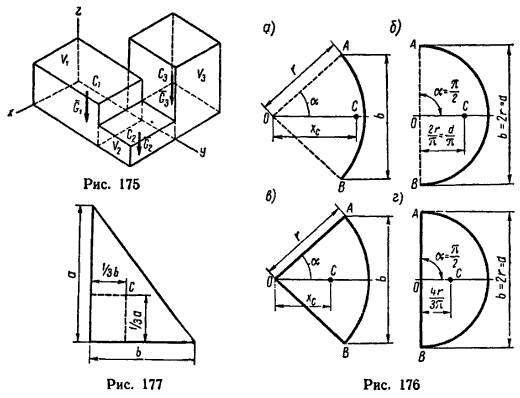
Если тело имеет вид фигуры, составленной из расположенных различным образом плоскостей или кривых поверхностей (рис. 174), то вес каждой плоскости (поверхности) можно представить так:
Gi = Fip,
где Fi – площади каждой поверхности, а p – вес единицы площади фигуры.
После подстановки этого значения Gi в формулы (1) получаем формулы координат центра тяжести фигуры, составленной из площадей :
xc = (∑ Fixi) / ∑ Fi;
(3) yc = (∑ Fiyi) / ∑ Fi;
zc = (∑ Fizi) / ∑ Fi.
Если же однородное тело можно разделить на простые части определенной геометрической формы (рис. 175), то вес каждой части
Gi = Viγ,
где Vi – объем каждой части, а γ – вес единицы объема тела.
После подстановки значений Gi в формулы (1) получаем формулы для определения координат центра тяжести тела, составленного из однородных объемов :
xc = (∑ Vixi) / ∑ Vi;
(4) yc = (∑ Viyi) / ∑ Vi;
zc = (∑ Vizi) / ∑ Vi.
При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.
Если известен радиус дуги r и центральный угол 2α, стягиваемый дугой и выраженный в радианах, то положение центра тяжести C (рис. 176, а) относительно центра дуги O определится формулой:
(5) xc = (r sin α)/α.
Если же задана хорда AB=b дуги, то в формуле (5) можно произвести замену
sin α = b/(2r)
и тогда
(5а) xc = b/(2α).
В частном случае для полуокружности обе формулы примут вид (рис. 176, б):
(5б) xc = OC = 2r/π = d/π.
Положение центра тяжести кругового сектора, если задан его радиус r (рис. 176, в), определяется при помощи формулы:
(6) xc = (2r sin α)/(3α).
Если же задана хорда сектора, то:
(6а) xc = b/(3α).
В частном случае для полукруга обе последние формулы примут вид (рис. 176, г)
(6б) xc = OC = 4r/(3π) = 2d/(3π).
Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты.
У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 177).
При решении задач на определение положения центра тяжести любого однородного тела, составленного либо из тонких стержней (линий), либо из пластинок (площадей), либо из объемов, целесообразно придерживаться следующего порядка:
1) выполнить рисунок тела, положение центра тяжести которого нужно определить. Так как все размеры тела обычно известны, при этом следует соблюдать масштаб;
2) разбить тело на составные части (отрезки линий или площади, или объемы), положение центров тяжести которых определяется исходя из размеров тела;
3) определить или длины, или площади, или объемы составных частей;
4) выбрать расположение осей координат;
5) определить координаты центров тяжести составных частей;
6) найденные значения длин или площадей, или объемов отдельных частей, а также координат их центров тяжести подставить в соответствующие формулы и вычислить координаты центра тяжести всего тела;
7) по найденным координатам указать на рисунке положение центра тяжести тела.
Видео:Центры тяжести прямоугольных треугольниковСкачать
§ 23. Определение положения центра тяжести тела, составленного из тонких однородных стержней
Видео:Определение центра тяжести сложной фигуры. СопроматСкачать

§ 24. Определение положения центра тяжести фигур, составленных из пластинок
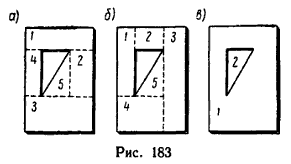
В последней задаче, а также в задачах, приведенных в предыдущем параграфе, расчленение фигур на составные части не вызывает особых затруднений. Но иногда фигура имеет такой вид, который позволяет разделить ее на составные части несколькими способами, например тонкую пластинку прямоугольной формы с треугольным вырезом (рис. 183). При определении положения центра тяжести такой пластинки ее площадь можно разделить на четыре прямоугольника (1, 2, 3 и 4) и один прямоугольный треугольник 5 – несколькими способами. Два варианта показаны на рис. 183, а и б.
Наиболее рациональным является тот способ деления фигуры на составные части, при котором образуется наименьшее их число. Если в фигуре есть вырезы, то их можно также включать в число составных частей фигуры, но площадь вырезанной части считать отрицательной. Поэтому такое деление получило название способа отрицательных площадей.
Пластинка на рис. 183, в делится при помощи этого способа всего на две части: прямоугольник 1 с площадью всей пластинки, как будто она целая, и треугольник 2 с площадью, которую считаем отрицательной.
Видео:Центр тяжести треугольникаСкачать

§ 25. Определение положения центра тяжести сечений, составленных из профилей стандартного проката
При решении задач, приведенных в этом параграфе, нужно пользоваться таблицами из ГОСТа на прокатную сталь: ГОСТ 8509–57, ГОСТ 8510–57, ГОСТ 8239–56, ГОСТ 8240–56.
Эти таблицы для каждого профиля содержат их размеры и площадь, а для уголков и швеллера, кроме того, – координаты центров тяжести.
Видео:Найдите центр тяжестиСкачать

§ 26. Определение положения центра тяжести тела, составленного из частей, имеющих простую геометрическую форму
Чтобы решать задачи на определение положения центра тяжести тела, составленного из частей, имеющих простую геометрическую форму, необходимо иметь навыки определения координат центра тяжести фигур, составленных из линий или площадей.
Видео:координаты центра тяжести треугольникаСкачать

Центры тяжести многоугольников и многогранников
Центром тяжести (или центром масс) некоторого тела называется точка, обладающая тем свойством, что если подвесить тело за эту точку, то оно будет сохранять свое положение.
Ниже рассмотрены двумерные и трёхмерные задачи, связанные с поиском различных центров масс — в основном с точки зрения вычислительной геометрии.
В рассмотренных ниже решениях можно выделить два основных факта. Первый — что центр масс системы материальных точек равен среднему их координат, взятых с коэффициентами, пропорциональными их массам. Второй факт — что если мы знаем центры масс двух непересекающихся фигур, то центр масс их объединения будет лежать на отрезке, соединяющем эти два центра, причём он будет делить его в то же отношении, как масса второй фигуры относится к массе первой.
Видео:Видеоурок 3. Определение центра тяжести.Скачать

Двумерный случай: многоугольники
На самом деле, говоря о центре масс двумерной фигуры, можно иметь в виду одну из трёх следующих задач:
- Центр масс системы точек — т.е. вся масса сосредоточена только в вершинах многоугольника.
- Центр масс каркаса — т.е. масса многоугольника сосредоточена на его периметре.
- Центр масс сплошной фигуры — т.е. масса многоугольника распределена по всей его площади.
Каждая из этих задач имеет самостоятельное решение, и будет рассмотрена ниже отдельно.
Центр масс системы точек
Это самая простая из трёх задач, и её решение — известная физическая формула центра масс системы материальных точек:
где 


В частности, если все точки имеют одинаковую массу, то координаты центра масс есть среднее арифметическое координат точек. Для треугольника эта точка называется центроидом и совпадает с точкой пересечения медиан:
Для доказательства этих формул достаточно вспомнить, что равновесие достигается в такой точке 

и, выражая отсюда 
Центр масс каркаса
Будем считать для простоты, что каркас однороден, т.е. его плотность везде одна и та же.
Но тогда каждую сторону многоугольника можно заменить одной точкой — серединой этого отрезка (т.к. центр масс однородного отрезка есть середина этого отрезка), с массой, равной длине этого отрезка.
Теперь мы получили задачу о системе материальных точек, и применяя к ней решение из предыдущего пункта, мы находим:
где 




Для треугольника можно показать следующее утверждение: эта точка является точкой пересечения биссектрис треугольника, образованного серединами сторон исходного треугольника. (чтобы показать это, надо воспользоваться приведённой выше формулой, и затем заметить, что биссектрисы делят стороны получившегося треугольника в тех же соотношениях, что и центры масс этих сторон).
Центр масс сплошной фигуры
Мы считаем, что масса распределена по фигуре однородно, т.е. плотность в каждой точке фигуры равна одному и тому же числу.
Случай треугольника
Утверждается, что для треугольника ответом будет всё тот же центроид, т.е. точка, образованная средним арифметическим координат вершин:
Случай треугольника: доказательство
Приведём здесь элементарное доказательство, не использующее теорию интегралов.
Первым подобное, чисто геометрическое, доказательство привёл Архимед, но оно было весьма сложным, с большим числом геометрических построений. Приведённое здесь доказательство взято из статьи Apostol, Mnatsakanian «Finding Centroids the Easy Way».
Доказательство сводится к тому, чтобы показать, что центр масс треугольника лежит на одной из медиан; повторяя этот процесс ещё дважды, мы тем самым покажем, что центр масс лежит в точке пересечения медиан, которая и есть центроид.
Разобьём данный треугольник 
Четыре получившихся треугольника подобны треугольнику 

Треугольники №1 и №2 вместе образуют параллелограмм, центр масс которого 


Пусть теперь вектор 





Наша цель — показать, что вектора 

Обозначим через 






Искомый центр масс 




Таким образом, вектор от вершины 





Таким образом, мы доказали, что вектора 



Более того, попутно мы доказали, что центроид делит каждую медиану в отношении 
Случай многоугольника
Перейдём теперь к общему случаю — т.е. к случаю мноугоугольника. Для него такие рассуждения уже неприменимы, поэтому сведём задачу к треугольной: а именно, разобьём многоугольник на треугольники (т.е. триангулируем его), найдём центр масс каждого треугольника, а затем найдём центр масс получившихся центров масс треугольников.
Окончательная формула получается следующей:
где 



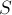
Триангуляция выпуклого многоугольника — тривиальная задача: для этого, например, можно взять треугольники 

Случай многоугольника: альтернативный способ
С другой стороны, применение приведённой формулы не очень удобно для невыпуклых многоугольников, поскольку произвести их триангуляцию — сама по себе непростая задача. Но для таких многоугольников можно придумать более простой подход. А именно, проведём аналогию с тем, как можно искать площадь произвольного многоугольника: выбирается произвольная точка 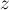


где 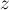
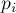




Видео:Урок 79. Центр масс тела и методы определения его положенияСкачать

Трёхмерный случай: многогранники
Аналогично двумерному случаю, в 3D можно говорить сразу о четырёх возможных постановках задачи:
- Центр масс системы точек — вершин многогранника.
- Центр масс каркаса — рёбер многогранника.
- Центр масс поверхности — т.е. масса распределена по площади поверхности многогранника.
- Центр масс сплошного многогранника — т.е. масса распределена по всему многограннику.
Центр масс системы точек
Как и в двумерном случае, мы можем применить физическую формулу и получить тот же самый результат:
который в случае равных масс превращается в среднее арифметическое координат всех точек.
Центр масс каркаса многогранника
Аналогично двумерному случаю, мы просто заменяем каждое ребро многогранника материальной точкой, расположенной посередине этого ребра, и с массой, равной длине этого ребра. Получив задачу о материальных точках, мы легко находим её решение как взвешенную сумму координат этих точек.
Центр масс поверхности многогранника
Каждая грань поверхности многогранника — двухмерная фигура, центр масс которой мы умеем искать. Найдя эти центры масс и заменив каждую грань её центром масс, мы получим задачу с материальными точками, которую уже легко решить.
Центр масс сплошного многогранника
Случай тетраэдра
Как и в двумерном случае, решим сначала простейшую задачу — задачу для тетраэдра.
Утверждается, что центр масс тетраэдра совпадает с точкой пересечения его медиан (медианой тетраэдра называется отрезок, проведённый из его вершины в центр масс противоположной грани; таким образом, медиана тетраэдра проходит через вершину и через точку пересечения медиан треугольной грани).
Почему это так? Здесь верны рассуждения, аналогичные двумерному случаю: если мы рассечём тетраэдр на два тетраэдра с помощью плоскости, проходящей через вершину тетраэдра и какую-нибудь медиану противоположной грани, то оба получившихся тетраэдра будут иметь одинаковый объём (т.к. треугольная грань разобьётся медианой на два треугольника равной площади, а высота двух тетраэдров не изменится). Повторяя эти рассуждения несколько раз, получаем, что центр масс лежит на точке пересечения медиан тетраэдра.
Эта точка — точка пересечения медиан тетраэдра — называется его центроидом. Можно показать, что она на самом деле имеет координаты, равные среднему арифметическому координат вершин тетраэдра:
(это можно вывести из того факта, что центроид делит медианы в отношении 
Таким образом, между случаями тетраэдра и треугольника принципиальной разницы нет: точка, равная среднему арифметическому вершин, является центром масс сразу в двух постановках задачи: и когда массы находится только в вершинах, и когда массы распределены по всей площади/объёму. На самом деле, этот результат обобщается на произвольную размерность: центр масс произвольного симплекса (simplex) есть среднее арифметическое координат его вершин.
Случай произвольного многогранника
Перейдём теперь к общему случаю — случаю произвольного многогранника.
Снова, как и в двумерном случае, мы производим сведение этой задачи к уже решённой: разбиваем многогранник на тетраэдры (т.е. производим его тетраэдризацию), находим центр масс каждого из них, и получаем окончательный ответ на задачу в виде взвешенной суммы найденных центров масс.
Видео:Практическая №5 Определение центра тяжести сложной фигурыСкачать

Презентация «Техническая механика. Центр тяжести»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
1
Центр тяжести простых геометрических фигур
2
1. Центр тяжести треугольника. Центр тяжести треугольника лежит в точке пересечения его медиан. Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: xc =(x1+x2+x3)/3 ; yc =(y1+y2+y3)/3.
3
2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис.). Координаты центра тяжести прямоугольника рассчитываются по формулам: xc =b/2 ; yc =h/2.
4
3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис.). Координаты центра тяжести полукруга рассчитываются по формулам: xc =D/2 ; yc =4R/3π.
5
4. Центр тяжести круга. Центр тяжести круга лежит в центре. Координаты центра тяжести круга рассчитываются по формулам: xc =R ; yc =R.
6
Пример 1: Определить положение центра тяжести фигуры, имеющей ось симметрии (размеры определены на схеме).
7
Решение:
Фигура имеет ось симметрии, на которой находится центр тяжести. Совместим с осью симметрии ось y, а ось x – с нижним основанием фигуры.
1. Разобьем фигуру произвольным образом на простые фигуры.
Наиболее рациональным из всех возможных способов деления фигуры на составные части является тот способ, при котором образуется наименьшее их число.
8
Дополнив фигуру до прямоугольника ABDE , разобьем ее на три части и определим площадь каждой (в см2):
1 – прямоугольник (большой ), (см2);
2 – прямоугольник (маленький), (см2);
3 – треугольник, (см2).
9
2. Определяем координаты центров тяжести составных частей:
Точка С1 – ЦТ первой фигуры имеет координаты: .
Точка С2 – ЦТ второй фигуры имеет координаты: .
Точка С3 – ЦТ третьей фигуры имеет координаты:
.
10
4. Координаты точки С — центра тяжести всей фигуры:
(см).
11
Пример 2: Определить положение центра тяжести фигуры, имеющей ось симметрии (размеры определены на схеме).
12
Решение:
1. Разобьем фигуру произвольным образом на простые фигуры (в данном случае на два прямоугольника) определим площадь каждой (в см2):
1 – прямоугольник, (см2);
2 – прямоугольник, (см2);
2. Определяем координаты центров тяжести составных частей:
Точка С1 – ЦТ первой фигуры имеет координаты: .
Точка С2 – ЦТ второй фигуры имеет координаты: .
13
4. Координаты точки С — центра тяжести всей фигуры:
Курс повышения квалификации
Охрана труда
- Сейчас обучается 104 человека из 42 регионов
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
- Сейчас обучается 357 человек из 63 регионов
Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 224 человека из 53 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Центр массСкачать

Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 558 229 материалов в базе
Другие материалы
- 17.06.2021
- 94
- 0
- 17.06.2021
- 48
- 0
- 17.06.2021
- 276
- 3
- 17.06.2021
- 157
- 0
- 17.06.2021
- 121
- 0
- 17.06.2021
- 47
- 0
- 17.06.2021
- 225
- 0
- 17.06.2021
- 59
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 17.06.2021 483
- PPTX 251.5 кбайт
- 1 скачивание
- Оцените материал:
Настоящий материал опубликован пользователем Сорокин Олег Владимирович. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 7 месяцев
- Подписчики: 0
- Всего просмотров: 5545
- Всего материалов: 33
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Центр тяжести. ЭкспериментСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
У 76% российских учителей оклад ниже МРОТ
Время чтения: 2 минуты
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
В Госдуме предложили ввести пост уполномоченного по правам учителей
Время чтения: 2 минуты
В Египте нашли древние школьные «тетрадки»
Время чтения: 1 минута
Петербургская учительница уволилась после чтения на уроке Введенского и Хармса
Время чтения: 3 минуты
В России могут объявить Десятилетие науки и технологий
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
🔍 Видео
Определение центра тяжести сложных сечений. Фигуры из ГОСТ.Скачать

Урок 1. Понятие центра тяжести. Демонстрации по физикеСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Как найти центр тяжести любой фигуры?Скачать

Определение центра тяжести плоской фигуры. Подробное объяснение. Сопромат для чайниковСкачать

Практическая работа по теме: Центр тяжестиСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Урок 80. Определение положения центра масс телаСкачать

Определение координат центра тяжести сложной фигуры (плоского сечения)Скачать

Определение центра тяжестиСкачать