Связи и реакции связей.
Связь осуществляется при помощи гибкого тела, нити, каната или троса. Реакция такой связи приложена к телу в точке прикрепленной к нему нити. Перечислим некоторые типы связей, предполагая, что они изготовлены из абсолютно твердых материалов и трение в местах их соприкосновения с рассматриваемыми телами отсутствует.
2)Шарнирное соединение тел (сферический шарнир, шарнирная опора неподвижная).
Система сходящихся сил.
Системой сходящихся сил наз-ют такую систему сил, линии действия которых пересекаются в одной точке. Сходящиеся системы сил могут быть пространственными или плоскими, расположенные в одной плоскости.
Сходящиеся системы сил могут быть пространственными и плоскими, т.е. расположенными в одной плоскости.
Предположим сначала, что на тело действуют две силы и , приложенные в одной точке A и образующие между собой угол . Равнодействующая этих двух сил, согласно аксиоме о параллелограмме сил, равна сумме этих сил, т.е. (рис.2.1,б)
. Модуль равнодействующей можно определить из треугольника ABC , заметив, что ?ABC=180. по теореме косинусов:
Момент силы относительно точки и оси.
Моментом силы относительно точки называется алгебраическая величина, равная произведению модуля силы на кратчайшее расстояние от точки до линии действия силы.Численное значение момента силы F относительно точки О будем обозначать mo(F). Тогдаmo(F) = ±Fh.Моментом силы относительно оси называется алгебраическая величина момента проекции этой силы на плоскость, перпендикулярную к данной оси, относительно точки пересечения этой плоскости с осью. Момент силы F относительно оси считается положительным, если наблюдатель, смотрящий с положительного направления оси, видит поворот, совершаемый составляющей Fxy силы F, происходящим против хода часовой стрелки.Из определения момента силы относительно оси следует
Момент силы относительно оси равен нулю, если сила параллельна оси или пересекает ее. В обоих случаях сила и ось лежат в одной плоскости. Момент имеет знак +, если сила стремится повернуть тело вокруг центра О против хода часовой стрелки. Знак -, если сила стремится повернуть тело по часовой стрелке. Отметим след. св-во момента сил: момент силы не изм-ся пори переносе точки приложения силы вдоль ее действия. Момент силы относительно центра равен 0 только тогда, когда сила равна 0 или когда линия действия силы проходит через центр О. Момент силы численно равен удвоенной площади треугольника.
9Приведение к равнодействующей силе сходящихся сил.
Сложить 2 силы или неск. сил – это значит найти их равнодействующую. Задача о сложении 2х сил, приложенных к тв. телу в одной точке решается на основании правила параллелограмма.
Системой сходящихся сил называют такую систему сил, линии действия которых пересекаются в одной точке
Сходящиеся системы сил могут быть пространственными и плоскими, т.е. расположенными в одной плоскости.
Предположим сначала, что на тело действуют две силы и , приложенные в одной точке A и образующие между собой угол . Равнодействующая этих двух сил, согласно аксиоме о параллелограмме сил, равна сумме этих сил, т.е.
.величина равнодействующей определится следующей формулой:
Для определения направления равнодействующей к воспользуемся обычными выражениями для направляющих косинусов:
Пара сил и ее момент.
Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на тело. Действие пары сил на тело сводится к вращательному эффекту. Для характеристики этого эффекта вводится понятие момента пары.:Моментом пары называется величина, равная взятому с соответствующим знаком произведению модуля одной из сил пары на ее плечо. Для равновесия пар сил, действующих на твердое тело, необходимо и достаточно, чтобы модуль векторного момента эквивалентной пары сил был равен нулю или чтобы векторный многоугольник, построенный на векторных моментах заданных пар сил, был замкнут.Момент пары считается положительным, если пара стремится повернуть тело против хода часовой стрелки, и отрицательным – если по ходу часовой стрелки.
Главный вектор и главный момент сил.
Главным вектором системы сил называют вектор, равный векторной сумме этих сил.
Главным моментом системы сил относительно точки O тела называют сумму векторных моментов всех сил системы относительно этой точки. Таким образом, основную теорему статики (теорему Пуансо) в краткой форме можно выразить так: Каждую систему сил можно привести к главному вектору и главному моменту относительно произвольного центра.
Видео:Момент силы. Определение, размерность и знаки. Плечо силыСкачать

Формулы для вычисления главного вектора и главного момента
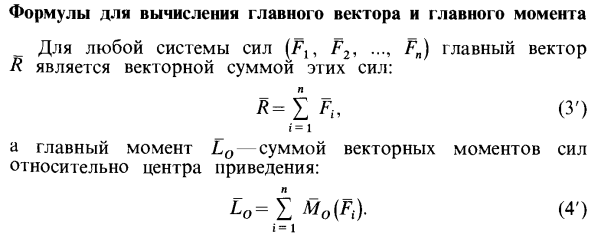


Видео:27. Теорема об изменении главного вектора количества движения механической системыСкачать

Формулы для вычисления главного вектора и главного момента
- Для любой системы сил Г1ЭГ2, FN главным вектором R является векторная сумма этих сил. 3 i = 1. Основным моментом Эо является сумма векторных моментов силы относительно центра торможения. 4 нынешний век i = 1 гора R изображается геометрически как замкнутый силовой полигон, построенный на заданной силе.
Поскольку угол поворота увеличивается со временем, он становится положительным, когда тело вращается против часовой стрелки, и отрицательным, когда тело вращается по часовой стрелке.Каковы необходимые и достаточные условия приведения тела в неупорядоченное состояние. Людмила Фирмаль
Для любой пространственной системы сил, которую мы получаем, мы проецируем обе стороны векторного уравнения 3 на координатные оси х = я х, .= Я. е лх, е лх. 5 = 1 1 = 1 1 = 1 Проекция определяет Косинус модуля основного вектора и его угол к координатным осям. СО8 х, ЛЯ = , СО8 6ЛЛ =А С05 все =. 6 Главный момент Lo геометрически изображается в виде замкнутого векторного многоугольника, построенного на векторном моменте силы относительно приведенного Центра.
- Обе части векторного уравнения 4 проецируются на декартову ось, используя соотношение между моментом силы относительно оси и проекцией этого момента вектора силы относительно точки на оси. LOx = Lx = E WX F, = E y Fiz z. fiy. 1 = 1 1 = 1 П0. = Ly = E L DG = E Zifix X. физ я = 1 я = л Кровать Loz = Л. = ЕК Фи = Е я = Л 1 = 1 Дж 7 Косинус угла между модулем и осью основного момента Координаты равны потому что Х, ло ЛК ЛО, потому что г, о лы ЛО, Ц0 Ео = В1 В0. 8.
В равновесном состоянии сила, действующая на твердое тело в равновесии на шероховатой поверхности объекта на равновесной шероховатой поверхности, есть еще неизвестная сила реакции, то есть сила трения на шероховатой поверхности. Людмила Фирмаль
Ось Oz перпендикулярна плоскости действия силовой плоской системы, а оси Ox и Oy в силовой плоскости, главный вектор R находится в плоскости Oxu, а следовательно, и в случае силовой плоской системы 9. ГХ = исправить е, ры = И. Ли, L2eO Л = Vy1 + ч, потому что Х, АР = х, С08 Я = Я, Д. Главный момент плоской системы сил перпендикулярен основному вектору, а следовательно, параллелен оси Oz. И затем… Lx = 0, Ly = 0, L0 = L, = ЗД = Z A 0 f , 10 i = 1 i = 1. Где Ло является ключевым моментом алгебраических.
Если вам потребуется заказать теоретическую механику вы всегда можете написать мне в whatsapp.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:§4.3. Главный вектор и главный момент сил инерцииСкачать

Техническая механика, Ст 21
методическая разработка
Группа Ст 21, 08.12.2020 г., 3 пара и 10.12.2020 г., 3 пара (4 часа) Лекция по теме: Основные понятия и определения сопротивления материалов
Видео:Прикладная механика (сопромат). Внутренние силыСкачать

Скачать:
| Вложение | Размер |
|---|---|
| osnovnye_ponyatiya_sopromata.docx | 143.11 КБ |
Видео:Принцип ДаламбераСкачать

Предварительный просмотр:
Основные понятия и определения «Сопротивления материалов»
Сопротивление материалов — наука, методами или способами которой находятся размеры и формы элементов конструкций, обеспечивающие этим элементам прочность, жесткость и устойчивость при наименьшем количестве материала, идущего на их изготовление.
Основным содержанием науки «Сопротивление материалов» является разработка методов расчета на прочность, устойчивость и жесткость элементов конструкций, с помощью которых можно выбрать материал и необходимые размеры элементов конструкции, оценить способность этих элементов сопротивляться внешним нагрузкам.
В отличие от дисциплины «Теоретическая механика», которая рассматривает тело как абсолютно твердое, «Сопротивление материалов» изучает его деформированное состояние. Однако, при решении своих задач данная дисциплина опирается на основы теоретической механики, высшей математики, физики, и изучение этой науки без знания основ перечисленных дисциплин невозможно.
В сопротивлении материалов закладывается фундамент для грамотного проектирования конструкций, элементов и деталей. В курсе дисциплины «Сопротивление материалов» изучаются основные виды деформированного состояния материалов, такие, как растяжение или сжатие, сдвиг, изгиб, кручение, сложное сопротивление, устойчивость сжатых стержней а также механика развития этих деформаций и приемы оценки прочности инженерных конструкций.
Явления, при которых происходят изменения формы и угловых размеров элементов конструкции называются деформацией . Деформация тела является следствием изменения средних расстояний между частицами (молекулами, атомами или ионами вещества тела).
Деформация , вызванная действиями на тело внешних сил, называется силовой , а деформация , вызванная изменением его внутренней температуры, — температурной . Совместную силовую и температурную деформации называют смешанной . Силы и изменения температуры, действующие на тело, принято называть внешними силовыми факторами . Приложение к конструкции внешних силовых факторов называется нагружением.
Оценка прочностной надежности элемента конструкции начинается с выбора расчетной модели (схемы). Моделью (схемой) называется совокупность представлений и зависимостей, описывающих рассматриваемый объект или явление.
1.2 Внешние силы
К внешним нагрузкам, действующим на конструкции и их элементы, относятся активные силы (нагрузки) и реакции внешних связей.
Нагрузки классифицируются по признакам:
1. По характеру приложения силы подразделяются на сосредоточенные и распределенные.
Сосредоточенными силами принято называть силы давления, передающиеся на элемент конструкции через площадку, размеры которой очень малы по сравнению с размерами всего элемента.
Распределенными силами называют силы, приложенные непрерывно на протяжении некоторой длины или площади конструкции. Распределенные нагрузки делятся на равномерно — распределенные и неравномерно распределенные (Рис. 1 (а, б)).
2. По характеру действия нагрузки подразделяются на статические и динамические .
Статические — это такие нагрузки, которые прикладываются плавно и постепенно. При статических нагрузках в конструкциях отсутствуют ускорения, если же в результате действия внешних нагрузок возникают большие ускорения, а, следовательно, и силы инерции, то имеют место динамические нагрузки. Примерами таких нагрузок могут служить внезапно приложенные, ударные и повторно переменные.
3. По времени действия внешние нагрузки подразделяются на постоянные и временные .
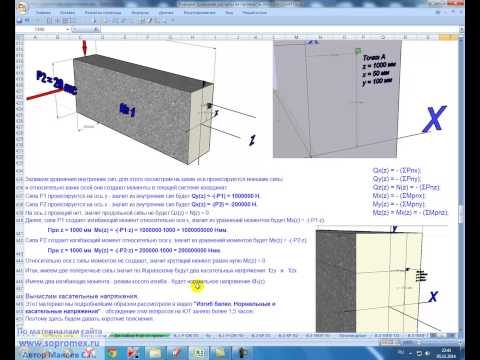
Внутренние силы — силы взаимодействия между частицами твердого тела, обеспечивающие его целостность и препятствующие его деформации. Как всякую систему сил, внутренние силы можно привести к центру тяжести сечения, так как они распределены в сечении стержня. В результате получим главный вектор R, главный момент M(R) всех внутренних сил, действующих в сечении стержня.
В процессе деформации элементов конструкции под действием внешней нагрузки происходит изменение взаиморасположения элементарных частиц элементов, в результате чего возникают внутренние силовые факторы, для определения которых применяют метод сечений.
1.4 Метод сечений
Задача метода сечений состоит в определении составляющих главного вектора R и главного момента M(R) системы сил упругости, действующих в главном поперечном сечении стержня (Рис. 2).
Метод сечений состоит из четырех операций, которые могут быть последовательно записаны начальными буквами своих названий — РОЗУ (разрезаем, отбрасываем, заменяем, уравновешиваем). Для решения задачи предпринимаем следующие действия:
1. Мысленно разрезаем сечением брус (стержень, вал или балку) на две части, например, левую и правую (Рис.2,а).
2. Одну из двух частей отбрасываем и рассматриваем оставшуюся, например, правую часть (Рис 2.б).
3. Заменяем действие отброшенной части на оставшуюся, системой сил упругости, непрерывно распределенной по сечению, которую приводим к главному вектору сил R и вектору главного момента М(R) внутренних сил.
Главный вектор внутренних сил, действующий в рассматриваемом сечении нагруженного стержня, равен сумме всех внешних сил, приложенных по одну сторону от рассматриваемого сечения:
Главный момент внутренних сил, действующих в рассматриваемом сечении нагруженного стержня, относительно центра тяжести сечения равен сумме моментов всех внешних сил, приложенных по одну сторону от рассматриваемого сечения:
Проецируя главный вектор и главный момент на координатные оси, получаем шесть составляющих: три составляющие главного вектора и три составляющие главного момента сил упругости, которые называются внутренними силовыми факторами:
где N-продольная сила ;
Q y , Q z –поперечные силы.
M(R) = M x +M y +M z ,
где M x = Т – крутящий момент;
M y и M z — изгибающие моменты.
4. Так как отсеченная часть должна находиться в равновесии, то есть быть уравновешенной , то должны удовлетворяться шесть уравнений статики:
Для характеристики закона распределения внутренних усилий по сечению стержня ввели числовую меру, названную напряжением.
Выделим вокруг точки В бесконечно малую площадку площадью 

Величина P ср называется средним напряжением и характеризует среднюю интенсивность внутренних сил, возникающих в поперечном сечении стержня.
Величина P называется истинным напряжением или просто напряжением в данной точке данного сечения стержня. Упрощенно можно сказать, что напряжением называется внутренняя сила, приходящаяся на единицу площади в данной точке данного рассматриваемого сечения:

Из формулы видно, что размерность напряжения [сила] / [площадь].
Единица измерения напряжения — Паскаль, сокращенно Па = Н/м 2 .
Так как при этом все реальные значения напряжений будут выражаться очень большими числами, то следует применять кратные значения единиц, допустим, МПА (мега Паскаль)= 10 6 Па.
Полное напряжение можно разложить на две составляющие (рис.4, а):
1) составляющую, нормальную к плоскости сечения стержня, которая обозначается 
2) составляющую, лежащую в плоскости сечения, которая обозначается 
Совокупность нормального и касательного напряжений, действующих по разным площадкам, проходящим через рассматриваемую точку, представляет напряженное состояние в данной точке данного сечения.
Для удобства представляют в виде двух составляющих по направлению координатных осей (рис. 4, б).
Принятые обозначения напряжений показаны на рисунке 4, б.
Для нормального напряжения ставится индекс, указывающий, какой координатной из осей параллельно данное напряжение. Растягивающее нормальное напряжение принято считать положительным, а сжимающее — отрицательным . Обозначения касательных напряжении снабжены двумя индексами: первый из них указывает, какой координатной оси параллельна нормаль к площадке действия данного напряжения, а второй показывает, какой оси параллельно само напряжение.
Раскладывание полного или истинного напряжения на нормальное и касательное напряжение имеет определенный физический смысл: нормальное напряжение возникает тогда, когда частицы материала стремятся отдалиться друг от друга или, наоборот, сблизиться, а касательные напряжения связаны со сдвигом частиц материала по плоскости рассматриваемого данного сечения.
Если мысленно вырезать вокруг любой точки конструкции элемент в виде бесконечно малого кубика, то по его граням в общем случае будут действовать напряжения, которые представлены на рисунке 5, а.
Если по граням кубика действуют одни только нормальные напряжения, то они называются главными напряжениями , а площадки, на которых они действуют, называются главными площадками .
Очевидно, что в каждой точке напряженного тела существуют три главные взаимно перпендикулярные площадки.
Главные напряжения обозначают 




Различные виды напряженного состояния классифицируются в зависимости от числа возникающих главных напряжений:
- если отличны от нуля все три главных напряжения, то напряженное состояние называется трехосным или объемным (рис. 5, б);
- если равно нулю одно из главных напряжений, а два других отличны от нуля, то напряженное состояние называется двухосным или плоским ;
- если равны нулю два главных напряжения, а третье отлично от нуля, то напряженное состояние называется одноосным или линейным .
1.6 Деформации и перемещения
Все конструкции под действием, приложенным к ним внешним нагрузкам, в той или иной степени деформируются, то есть изменяют свои размеры, форму или и то и другое одновременно.
Изменение линейных размеров конструкции или её элементов называется линейной деформацией, а изменение угловых размеров — угловой деформацией.
Увеличение размеров конструкции называется удлинением , а уменьшение размеров – укорочением , а если деформации изменяются по объему тела, то говорят о деформации в данной точке тела, в определенном направлении.
Совокупность линейных деформаций по различным направлениям и угловых деформаций по различным плоскостям, проходящим через рассматриваемую точку данного сечения, представляет деформированное состояние в данной точке данного сечения.
Если на поверхности конструкции, вблизи исследуемой точки, нанести весьма малый прямоугольник ABCD ( рис. 6, а), то в результате деформации, этот прямоугольник в общем случае примет вид параллелограмма A ’ B ’ C ’ D ’ (рис. 6, б).
Длины сторон прямоугольника изменятся (увеличатся или уменьшатся), а стороны повернутся по отношению к первоначальному положению на некоторый угол.
Если, например, длина стороны BC изменится на величину ∆l, то отношение называется средней линейной деформацией (в данном случае средним удлинением) в точке B:
Изменение первоначального прямого угла между сторонами рассматриваемого прямоугольника:
и будет характеризовать угловую деформацию (угол сдвига) в данной точке данного сечения.
Опыт показывает, что деформации, как линейные, так и угловые, могут или полностью исчезнуть, или исчезнуть только частично после снятия нагрузки (в зависимости от материала и величины нагружения).
Деформации, которые исчезают после разгрузки конструкции, называются упругими , а свойство тела принимать после разгрузки свою первоначальную форму называется упругостью .
Деформации, сохраняемые конструкцией после удаления нагрузки, называются остаточными или пластическими , а свойство материалов сохранять остаточные деформации называется пластичностью .
Зная деформации во всех точках конструкции и условия её закрепления, можно определить перемещения всех точек тела, то есть указать их новое положение после деформации. Для нормальной эксплуатации конструкции деформации его отдельных элементов должны быть, обычно, упругими, а вызванные ими перемещения не должны по абсолютной величине превышать определенных допускаемых значений. Эти условия, выраженные в форме тех или иных уравнений, носят название условия жесткости . В некоторых случаях допускаются небольшие пластические деформации для конструкций, выполненных из железобетона, пластмасс и для конструкций из металла, подверженных действию высоких температур.
1.7 Основные допущения (гипотезы), принятые в курсе дисциплины
1. Материал конструкции считается сплошным и однородным, то есть допуcкается, что однородная масса заполняет весь объем тела сплошным образом без пустот.
2. Материал тела изотропен, то есть свойства материала по всем направлениям одинаковы.
3. Свойство малого элемента, выделенного в любом месте рассматриваемого сечения тела, те же, что и всего тела.
4. Деформации конструкции предполагаются настолько малыми, что можно не учитывать их влияние на взаимное расположение нагрузок, а также бесконечно малых перемещений его по сравнению с геометрическими размерами самой конструкции (принцип начальных размеров).
5. Справедлив принцип независимости действия сил (принцип суперпозиций) , результат воздействия на конструкцию системы нагрузок равен сумме результатов воздействия каждой нагрузки в отдельности.
6. Поперечные сечения бруса, плоские и нормальные к оси бруса до приложения к нему нагрузки, остаются плоскими и нормальными к его оси при действии нагрузки ( гипотеза плоских сечений или гипотеза Бернулли ).
7. Принцип, утверждающий, что в точках тела, достаточно удалённых от места приложения сил, внутренние силы практически не зависят от характера распределения внешних сил, называется принципом Сен-Венана .
8. Принцип, утверждающий, что деформации материала конструкции в каждой его точке прямо пропорциональны напряжениям в данной точке носит название закона Гука .
Видео:Основы Сопромата. Внутренние силы. Эпюры внутренних усилий для пространственного стержняСкачать

По теме: методические разработки, презентации и конспекты
мультимедийная презентация к уроку технической механики. тема:Силовые факторы механики.
Презентация 1 выполнена для демонстрации на первом уроке технической механики. На слайдах в конспективной форме приводятся определения силы, момента силы относительно точки, пары сил. Средс.
Рабочая программа Техническая механика для специальности «Техническое обслуживание и ремонт автомобильного транспорта»
Рабочая программа учебной дисциплины «Техническая механика» является частью основной профессиональной образовательной программы в соответствии с ФГОС по специальности СПО 190631 «Техническое обслужива.
СЦЕНАРИЙ ПРОВЕДЕНИЯ КОНКУРСА «ЗНАТОКИ ТЕХНИЧЕСКОЙ МЕХАНИКИ» ПО ДИСЦИПЛИНЕ «ТЕХНИЧЕСКАЯ МЕХАНИКА»
Сценарий конкурса «Знатоки технической механики» по дисциплине «Техническая механика» отражают полный комплекс материала по подготовке и проведению данной интеллектуальной игры во внеурочное время.Дан.
Контрольно-измерительные материалы по дисциплине: «Техническая механика с основами технических измерений»
Итоговая аттестация в виде экзамена Форма контроля:В результате итоговой аттестации обучающийся должен уметь:- Производить расчет прочности несложных деталей .
РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ ОП.02 ТЕХНИЧЕСКАЯ МЕХАНИКА для специальности 23.02.07 «ТЕХНИЧЕСКОЕ ОБСЛУЖИВАНИЕ И РЕМОНТ ДВИГАТЕЛЕЙ, СИСТЕМ И АГРЕГАТОВ АВТОМОБИЛЕЙ»
РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ ОП.02 ТЕХНИЧЕСКАЯ МЕХАНИКА для специальности 23.02.07 «ТЕХНИЧЕСКОЕ ОБСЛУЖИВАНИЕ И РЕМОНТ ДВИГАТЕЛЕЙ, СИСТЕМ И АГРЕГАТОВ АВТОМОБИЛЕЙ» разработана с учетом.
КИМ по УД «Техническая механика» для специальности 23.02.04 «Техническая эксплуатация подъемно-транспортных, строительных и дорожных машин и оборудования (по отраслям)»
КИМ по УД «Техническая механика".
Рабочая программа учебной дисциплины ОП.03 Техническая механика с основами технических измерений (35.01.13)
Рабочая программа учебной дисциплины ОП.03 Техническая механика с основами технических измирений разработана на основе федерального государственного образовательного стандарта по профессии среднего пр.
📹 Видео
Консультация к устному экзамену. Механика. Часть 4: "Вращение твердых тел"Скачать

Приведение системы сил к простейшему видуСкачать

Геометрия масс. Теорема о движении центра массСкачать

Урок 94. Вычисление моментов инерции телСкачать

Внутренние силы. Определение. Метод сечений. Сопромат - Тайные Знания 6.Скачать
Момент импульса и момент силы относительно точки и оси | Студенты, абитуриенты МФТИ | Вуз. физика #1Скачать

Урок 109. Момент импульса. Закон сохранения момента импульсаСкачать

СКД Лекция 14 Теорема об изменении кинетического моментаСкачать

Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

Принцип Даламбера и метод кинетостатики (лекция + решение задачи)Скачать

СМ -1.7 Метод сечений, внутренние силовые факторы (ВСФ)Скачать

Внутренние силовые факторы и напряженияСкачать

14.1. Теорема о движении центра массСкачать

Момент силыСкачать















