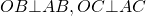Отрезки касательных к окружности проведенные из одной точки равны доказательство

Рассмотрим, какими свойствами обладают отрезки касательных к окружности, проведенные из одной точки.

(Свойство касательных, проведенных из одной точки)

Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

AB=AC ∠BAO=∠CAO

Дано: окружность (O;R),

AB и AC — касательные к окружности (O;R),

B, C — точки касания.

Доказать: AB=AC, ∠BAO=∠CAO.

Следовательно, треугольники ABO и ACO — прямоугольные. У них

1) катеты OB=OC (как радиусы)

2) гипотенуза OA — общая сторона.

Из равенства треугольников следует равенство соответствующих сторон:

Отрезки и прямые, связанные с окружностью. Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Свойства хорд и дуг окружности

Теоремы о длинах хорд, касательных и секущих

Доказательства теорем о длинах хорд, касательных и секущих

Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Фигура	Рисунок	Определение и свойства
Окружность
Круг
Радиус
Хорда
Диаметр
Касательная
Секущая

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды		Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности		Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Фигура	Рисунок	Теорема
Пересекающиеся хорды
Касательные, проведённые к окружности из одной точки
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

Об отрезках касательной к окружности

Разделы: Математика

Чаще всего именно геометрические задачи вызывают затруднения у абитуриентов, выпускников, участников математических олимпиад. Если посмотреть статистику ЕГЭ 2010 года, то видно, что к геометрической задаче С4 приступило около 12% участников, а получило полный балл только 0,2% участников, а в целом задача оказалась самой сложной из всех предложенных.

Очевидно, что чем раньше мы предложим школьникам красивые или неожиданные по способу решения задачи, тем больше вероятность заинтересовать и увлечь всерьёз и надолго. Но, как же трудно найти интересные и сложные задачи на уровне 7 класса, когда только начинается систематическое изучение геометрии. Что можно предложить интересующемуся математикой школьнику, знающему только признаки равенства треугольников, свойства смежных и вертикальных углов? Однако, можно ввести понятие касательной к окружности, как прямой, имеющей с окружностью одну общую точку; принять, что радиус, проведённый в точку касания, перпендикулярен касательной. Конечно, стоит рассмотреть все возможные случаи расположения двух окружностей и общих касательных к ним, которых можно провести от нуля до четырёх. Доказав ниже предложенные теоремы, можно значительно расширить набор задач для семиклассников. При этом попутно доказать важные или просто интересные и занимательные факты. Причём, поскольку многие утверждения не входят в школьный учебник, то обсуждать их можно и на занятиях кружка и с выпускниками при повторении планиметрии. Актуальными эти факты оказались в прошлом учебном году. Так как многие диагностические работы и сама работа ЕГЭ содержали задачу, для решения которой необходимо было использовать доказываемое ниже свойство отрезка касательной.

Т₁ Отрезки касательных к окружности, проведённые из
одной точки равны (рис. 1)

Вот именно с теоремой можно сначала познакомить семиклассников.
В процессе доказательства использовали признак равенства прямоугольных треугольников, сделали вывод о том, что центр окружности лежит на биссектрисе угла ВСА.
Попутно вспомнили, что биссектриса угла есть геометрическое место точек внутренней области угла, равноудалённых от его сторон. На этих доступных даже только начинающим изучать геометрию фактах основывается решение уже далеко нетривиальной задачи.

1. Биссектрисы углов А, В и С выпуклого четырёхугольника АВСD пересекаются в одной точке. Лучи АВ и DC пересекаются в точке Е, а лучи
ВС и АD в точке F. Докажите, что у невыпуклого четырёхугольника AECF суммы длин противоположных сторон равны.

Решение (рис. 2). Пусть О – точка пересечения данных биссектрис. Тогда О равноудалена от всех сторон четырёхугольника АВСD, то есть
является центром окружности вписанной в четырёхугольник. По теореме 1 верны равенства: AR = AK, ER = EP, FT = FK. Почленно сложим левые и правые части, получим верное равенство:

Рассмотрим необычную по формулировке задачу, для решения которой достаточно знание теоремы 1.

2. Существует ли n-угольник, стороны которого последовательно 1, 2, 3, …, n, в который можно вписать окружность?

Решение. Допустим, такой n-угольник существует. А₁А₂ =1, …, А_n-1А_n = n – 1, А_nА₁ = n. B₁, …, B_n – соответствующие точки касания. Тогда по теореме 1 A₁B₁ = A₁B_n Можно обобщить этот факт – суммы сторон описанного чётноугольника, взятых через одну, равны. Например, для шестиугольника ABCDEF верно: AB + CD + EF = BC + DE + FА.

3. МГУ. В четырёхугольнике ABCD расположены две окружности: первая окружность касается сторон AB, BC и AD, а вторая – сторон BC, CD и AD. На сторонах BC и AD взяты точки E и F соответственно так, отрезок EF касается обеих окружностей, а периметр четырёхугольника ABEF на 2p больше периметра четырёхугольника ECDF. Найти AB, если CD = a.

Решение (рис. 1). Так как четырёхугольники ABEF и ECDF вписанные, то по теореме 2 Р_ABEF = 2(AB + EF) и Р_ECDF = 2(CD + EF), по условию

Р_ABEF – Р_ECDF = 2(AB + EF) – 2(CD + EF) = 2p. AB – CD = p. АВ = а + р.

Опорная задача 1. Прямые АВ и АС – касательные в точках В и С к окружности с центром в точке О. Через произвольную точку Х дуги ВС
проведена касательная к окружности, пересекающая отрезки АВ и АС в точках М и Р соответственно. Докажите, что периметр треугольника АМР и величина угла МОР не зависят от выбора точки Х.

Решение (рис. 5). По теореме 1 МВ = МХ и РС = РХ. Поэтому периметр треугольника АМР равен сумме отрезков АВ и АС. Или удвоенной касательной, проведённой к вневписанной окружности для треугольника АМР. Величина угла МОР измеряется половиной величины угла ВОС, который не зависит от выбора точки Х.

Опорная задача 2а. В треугольник со сторонами а, b и c вписана окружность, касающаяся стороны АВ и точке К. Найти длину отрезка АК.

Решение (рис. 6). Способ первый (алгебраический). Пусть АК = АN = x, тогда BK = BM = c – x, CM = CN = a – c + x. АС = АN + NC, тогда можем составить уравнение относительно х: b = x + (a – c + x). Откуда .

Способ второй (геометрический). Обратимся к схеме. Отрезки равных касательных, взятые по одному, в сумме дают полупериметр
треугольника. Красный и зелёный составляют сторону а. Тогда интересующий нас отрезок х = р – а. Безусловно, полученные результаты совпадают.

Опорная задача 2б. Найти длину отрезка касательной АК, если К – точка касания вневписанной окружности со стороной АВ. Решение (рис. 7). АК = АM = x, тогда BK = BN = c – x, CM = CN. Имеем уравнение b + x = a + (c – x). Откуда . Заметим, что из опорной задачи 1 следует, что СМ = р _{Δ АВС}. b + x = p; х = р – b. Полученные формулы имеют применение в следующих задачах.

4. Найдите радиус окружности, вписанной в прямоугольный треугольник с катетами а, b и гипотенузой с. Решение (рис. 8). Так как OMCN – квадрат, то радиус вписанной окружности равен отрезку касательной CN. .

5. Докажите, что точки касания вписанной и вневписанной окружности со стороной треугольника симметричны относительно середины этой стороны.

Решение (рис. 9). Заметим, АК – отрезок касательной вневписанной окружности для треугольника АВС. По формуле (2) . ВМ – отрезок касательной вписанной окружности для треугольника АВС. По формуле (1) . АК = ВМ, а это и означает, что точки К и М равноудалены от середины стороны АВ, что и требовалось доказать.

6. К двум окружностям проведены две общие внешние касательные и одна внутренняя. Внутренняя касательная пересекает внешние в точках А, В и касается окружностей в точках А₁ и В₁. Докажите, что АА₁ = ВВ₁.

Решение (рис. 10). Стоп… Да что тут решать? Это же просто другая формулировка предыдущей задачи. Очевидно, что одна из окружностей является вписанной, а другая вневписанной для некоего треугольника АВС. А отрезки АА₁ и ВВ₁ соответствуют отрезкам АК и ВМ задачи 5. Примечательно, что задача, предлагавшаяся на Всероссийской олимпиаде школьников по математике, решается столь очевидным образом.

7. Стороны пятиугольника в порядке обхода равны 5, 6, 10, 7, 8. Доказать, что в этот пятиугольник нельзя вписать окружность.

Решение (рис. 11). Предположим, что в пятиугольник АВСDE можно вписать окружность. Причём стороны AB, BC, CD, DE и ЕA равны соответственно 5, 6, 10, 7 и 8. Отметим последовательно точки касания – F, G, H, M и N. Пусть длина отрезка AF равна х.

Но, AF = AN. То есть 10 – х = х; х = 5. Однако, отрезок касательной AF не может равняться стороне АВ. Полученное противоречие и доказывает, что в данный пятиугольник нельзя вписать окружность.

8. В шестиугольник вписана окружность, его стороны в порядке обхода равны 1, 2, 3, 4, 5. Найти длину шестой стороны.

Решение. Конечно, можно отрезок касательной обозначить за х, как и в предыдущей задаче, составить уравнение и получить ответ. Но, гораздо эффективнее и эффектнее использовать примечание к теореме 2: суммы сторон описанного шестиугольника, взятых через одну, равны.

Тогда 1 + 3 + 5 = 2 + 4 + х, где х – неизвестная шестая сторона, х = 3.

9. МГУ, 2003 г. химический факультет, № 6(6). В пятиугольник АВСDE вписана окружность, Р – точка касания этой окружности со стороной ВС. Найдите длину отрезка ВР, если известно, что длины всех сторон пятиугольника есть целые числа, АВ = 1, СD = 3.

Решение (рис.12). Так как длины всех сторон являются целыми числами, то равны дробные части длин отрезков BT, BP, DM, DN, AK и AT. Имеем, АТ + ТВ = 1, и дробные части длин отрезков AT и TB равны. Это возможно только тогда, когда АТ + ТВ = 0,5. По теореме 1 ВТ + ВР.
Значит, ВР = 0,5. Заметим, что условие СD = 3 оказалось невостребованным. Очевидно, авторы задачи предполагали какое-то другое решение. Ответ: 0,5.

10. В четырёхугольнике ABCD AD = DC, AB = 3, BC = 5. Окружности, вписанные в треугольники ABD и CBD касаются отрезка BD в точках M и N соответственно. Найти длину отрезка MN.

Решение (рис. 13). MN = DN – DM. По формуле (1) для треугольников DBA и DBС соответственно, имеем:

11. В четырёхугольник ABCD можно вписать окружность. Окружности, вписанные в треугольники ABD и CBD имеют радиусы R и r соответственно. Найти расстояние между центрами этих окружностей.

Решение (рис. 13). Так как по условию четырёхугольник ABCD вписанный, по теореме 2 имеем: AB + DC = AD + BC. Воспользуемся идеей решения предыдущей задачи. . Это означает, что точки касания окружностей с отрезком DM совпадают. Расстояние между центрами окружностей равно сумме радиусов. Ответ: R + r.

Фактически доказано, что условие – в четырёхугольник ABCD можно вписать окружность, равносильно условию – в выпуклом четырехугольнике ABCD окружности, вписанные в треугольники ABC и ADC касаются друг друга. Верно обратное.

Доказать эти два взаимно-обратных утверждения предлагается в следующей задаче, которую можно считать обобщением данной.

12. В выпуклом четырехугольнике ABCD (рис. 14) окружности, вписанные в треугольники ABC и ADC касаются друг друга. Докажите, что окружности, вписанные в треугольники ABD и BDC также касаются друг друга.

13. В треугольнике АВС со сторонами а, b и c на стороне ВС отмечена точка D так, что окружности, вписанные в треугольники АВD и ACD касаются отрезка AD в одной точке. Найти длину отрезка BD.

Решение (рис. 15). Применим формулу (1) для треугольников ADC и ADB, вычислив DM двумя

Оказывается, D – точка касания со стороной ВС окружности, вписанной в треугольник АВС. Верно обратное: если вершину треугольника соединить с точкой касания вписанной окружности на противоположной стороне, то окружности, вписанные в получившиеся треугольники, касаются друг друга.

14. Центры О₁, О₂ и О₃ трёх непересекающихся окружностей одинакового радиуса расположены в вершинах треугольника. Из точек О₁, О₂, О₃ проведены касательные к данным окружностям так, как показано на рисунке.

Известно, что эти касательные, пересекаясь, образовали выпуклый шестиугольник, стороны которого через одну покрашены в красный и синий цвета. Докажите, что сумма длин красных отрезков равна сумме длин синих.

Решение (рис. 16). Важно понять, как использовать тот факт, что заданные окружности имеют одинаковые радиусы. Заметим, что отрезки ВR и DМ равны, что следует из равенства прямоугольных треугольников О₁ВR и O₂BM. Аналогично DL = DP, FN = FK. Почленно складываем равенства, затем вычитаем из полученных сумм одинаковые отрезки касательных, проведенных из вершин А, С, и Е шестиугольника ABCDEF: АR и AK, CL и CM, EN и EP. Получаем требуемое.

Вот пример задачи по стереометрии, предлагавшейся на XII Международном математическом турнире старшеклассников “Кубок памяти А. Н. Колмогорова”.

16. Дана пятиугольная пирамида SA₁A₂A₃A₄A₅. Существует сфера w , которая касается всех ребер пирамиды и другая сфера w ₁, которая касается всех сторон основания A₁A₂A₃A₄A₅ и продолжений боковых рёбер SA₁, SA₂, SA₃, SA₄, SA₅ за вершины основания. Докажите, что вершина пирамиды равноудалена от вершин основания. (Берлов С. Л., Карпов Д. В.)

Решение. Пересечение сферы w с плоскостью любой из граней сферы – это вписанная окружность грани. Пересечение сферы w ₁ с каждой из граней SA_iA_i+1 – вневписанная окружность, касающаяся стороны A_iA_i+1 треугольника SA_iA_i+1 и продолжений двух других сторон. Обозначим точку касания w ₁ с продолжением стороны SA_i через B_i. По опорной задаче 1 имеем, что SB_i = SB_i+1 = p_SAiAi+1 , следовательно, периметры всех боковых граней пирамиды равны. Обозначим точку касания w со стороной SA_i через С_i. Тогда SC₁ = SC₂ = SC₃ = SC₄ = SC₅= s,
так как отрезки касательных равны. Пусть C_iA_i = a_i. Тогда p_SAiAi+1 = s+a_i+a_i+1, и из равенства периметров следует, что a₁ = a₃ = a₅ = a₂ = a₄, откуда SA₁ = SA₂ = SA₃ = SA₄ = SA₅.

17. ЕГЭ. Диагностическая работа 8.12.2009 г, С–4. Дана трапеция ABCD, основания которой BC = 44, AD = 100, AB = CD = 35. Окружность, касающаяся прямых AD и AC, касается стороны CD в точке K. Найдите длину отрезка CK.

Найдем диагональ AC. Опустим из вершин B и C на сторону AD перпендикуляры BE и CF соответственно. AE = FD, так как трапеция равнобедренная. BCFE – прямоугольник.

Возможны две геометрические конфигурации.

Первый случай (рис. 18): окружность вписана в треугольник ACD.

По формуле (1)

Второй вариант (рис.19): окружность касается продолжений сторон AC и AD за точками C и D соответственно и отрезка CD.

По формуле (2)

18. ЕГЭ. 4.6. 2010 г. В треугольнике АВС АВ = 13, ВС = 11, СА = 9. Точка D лежит на прямой АС, причём АD : DС = 1 : 9. Окружности, вписанные в каждый из треугольников ВDС и ВDА, касаются стороны ВD в точках Е и F. Найдите длину отрезка EF.

Решение. Возможны два случая (рис. 20 и рис. 21). По формуле (1) найдём длины отрезков DE и DF.

В первом случае AD = 0,1АС, СD = 0,9AC. Во втором – AD = 0,125АС, СD = 1,125AC. Подставляем данные и получаем ответ: 4,6 или 5,5.

Задачи для самостоятельного решения/

1. Периметр равнобедренной трапеции, описанной около окружности равен 2р. Найдите проекцию диагонали трапеции на большее основание. (1/2р)

2. Открытый банк задач ЕГЭ по математике. В4. К окружности, вписанной в треугольник ABC (рис. 22), проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника. (24)

3. В треугольник АВС вписана окружность. MN – касательная к окружности, M Î АС, N Î ВС, ВС = 13, АС = 14, АВ = 15. Найдите периметр треугольника MNC. (12)

4. К окружности, вписанной в квадрат со стороной а, проведена касательная, пересекающая две его стороны. Найдите периметр отсечённого треугольника. (а)

5. Окружность вписана в пятиугольник со сторонами а, d, c, d и e. Найдите отрезки, на которые точка касания делит сторону, равную а.

Ответ:

6. В треугольник со сторонами 6, 10 и 12 вписана окружность. К окружности проведена касательная так, что она пересекает две большие стороны. Найдите периметр отсечённого треугольника. (16)

7. CD – медиана треугольника ABC. Окружности, вписанные в треугольники ACD и BCD, касаются отрезка CD в точках M и N. Найдите MN, если АС – ВС = 2. (1)

8. В треугольнике АВС со сторонами а, b и c на стороне ВС отмечена точка D. К окружностям, вписанным в треугольники АВD и ACD, проведена общая касательная, пересекающая AD в точке М. Найти длину отрезка АМ. (Длина АМ не зависит от положения точки D и
равна ½ (c + b – a))

9. В прямоугольный треугольник вписана окружность радиуса а. Радиус окружности, касающейся гипотенузы и продолжений катетов, равен R. Найдите длину гипотенузы. (R – a)

10. В треугольнике АВС известны длины сторон: АВ = с, АС = b, ВС = а. Вписанная в треугольник окружность касается стороны АВ в точке С₁. Вневписанная окружность касается продолжения стороны АВ за точку А в точке С₂. Определите длину отрезка С₁С₂. (b)

11. Найдите длины сторон треугольника, разделённых точкой касания вписанной окружности радиуса 3 см на отрезки 4 см и 3 см. (7, 24 и 25 см в прямоугольном треугольнике)

12. Соросовская олимпиада 1996 г, 2 тур, 11 класс. Дан треугольник АВС, на сторонах которого отмечены точки А₁, В₁, С₁. Радиусы окружностей вписанных в треугольники АС₁В₁, ВС₁А₁, СА₁В₁ равны по r. Радиус окружности, вписанной в треугольник А₁В₁С₁ равен R. Найти радиус окружности, вписанной в треугольник АВС. (R + r).

Задачи 4–8 взяты из задачника Гордина Р. К. “Геометрия. Планиметрия.” Москва. Издательство МЦНМО. 2004.

🎥 Видео