Соотношение периметра и площади четырехугольника

Четырехугольник – это многоугольник, у которого четыре вершины и четыре стороны. Четырехугольниками являются ромб, прямоугольник, квадрат, параллелограмм и трапеция.

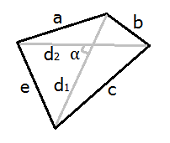
Любой четырехугольник характеризуется сторонами и диагоналями d1 и d2 (см. рисунок). Также при решении задач может понадобиться угол α между диагоналями. Именно эти характеристики используются в формулах четырехугольника при вычислении площади и периметра.

Формула периметра четырехугольника

Периметр P четырехугольника можно получить, зная его стороны:

Формулы площади четырехугольника

Площадь четырехугольника S можно вычислить, зная его диагонали и угол α между ними:

Поделитесь статьей с одноклассниками «ЧЕТЫРЕХУГОЛЬНИК формулы площади и периметра».

Соотношение периметра и площади четырехугольника

Изучение зависимостей площадей и периметров в четырехугольниках

Автор работы награжден дипломом победителя III степени

С понятием периметр и площадь я познакомилась в 3 классе. Э ти важные понятия необходимы человеку на протяжении всей его жизни. Деятельность строителей, инженеров, земледельцев и представителей других профессий немыслима без прочных знаний по этой теме.

Актуальность темы . Понятия «площади» и «периметра» необходимы человеку в окружающей жизни постоянно, например – сделать ремонт в доме или красиво оформить клумбу на даче. И то и другое понятие связывают стороны многоугольников. Знание зависимостей между этими величинами очень важно для современного человека.

Цель проекта: установить некоторые зависимости между площадью и периметром, увидеть их применение в практических ситуациях.

Задачи:повторить понятия по теме исследования, а именно: «площадь фигуры» и «периметр фигуры»; провести необходимые исследования и опыты; сделать выводы о зависимости площадей и периметров ; рассмотреть практическое применение полученных результатов.

Определение предмета исследования. Что нужно выяснить:

Как связаны периметры и площади прямоугольников?

Зависит ли площадь прямоугольника от его периметра?

Какой прямоугольник имеет наибольшую площадь при заданном периметре?

Если известен периметр прямоугольника, то нельзя ли однозначно установить его площадь?

Что можно сказать о зависимости площади квадрата от его периметра?

Проблема. Никаких зависимостей связывающих площади и периметры фигур мы пока не изучили.

Вот, самый простой пример, который задает проблему: «Есть два участка земли 80 м на 100 м и 50 м на 160 м. Вроде, площадь одинаковая – 8000 м 2 , а первый участок выгоднее купить, чем второй, забор то на 60 м короче строить». С точки зрения математики, все ясно, а вот логически – странно, периметр это замкнутая воображаемая нить, и то, что внутри нее не должно меняться, как ее не крути. Почему есть разница в периметрах? Так все-таки, есть ли какие-то зависимости, или площадь и периметр никак не зависят друг от друга?

Гипотеза. Предполагаем, что некоторые зависимости существуют. С изменением длины одной из сторон прямоугольника при заданном периметре изменится и площадь этого прямоугольника. Можно даже предположить, что если площадь больше, то периметр больше. Если у одной фигуры больше периметр, чем у второй, то её площадь больше, меньше или по-разному?

Периметр – величина, равная сумме длин всех сторон многоугольника.

Площадь фигуры – величина, показывающая сколько места занимает фигура на плоскости.

Свойства площадей нам тоже известны:

Равные фигуры имеют равные площади.

Площадь всей фигуры равна сумме площадей ее частей.

За единицу площади принимают площадь квадрата, сторона которого равна единичному отрезку.

Исследования начнем с простой и хорошо знакомой нам фигуры – прямоугольника.

Заполним таблицу, считая площадь одной клеточки равной 1 см 2

Площади четырехугольников

Формулы для площадей четырехугольников

Вывод формул для площадей четырехугольников

Вывод формулы Брахмагупты для площади вписанного четырехугольника

В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:

которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.

Формулы для площадей четырехугольников

a и b – смежные стороны

d – диагональ,
φ – любой из четырёх углов между диагоналями

Получается из верхней формулы подстановкой d=2R

R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

a – сторона,
h_a – высота, опущенная на эту сторону

a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

a – сторона квадрата

Получается из верхней формулы подстановкой d = 2R

a – сторона,
h_a – высота, опущенная на эту сторону

a – сторона,
φ – любой из четырёх углов ромба

r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

a и b – основания,
h – высота

φ – любой из четырёх углов между ними

a и b – основания,
c и d – боковые стороны

a и b – неравные стороны,
φ – угол между ними

a и b – неравные стороны,
φ₁ – угол между сторонами, равными a ,
φ₂ – угол между сторонами, равными b .

a и b – неравные стороны,
r – радиус вписанной окружности

φ – любой из четырёх углов между ними

,

a, b, c, d – длины сторон четырёхугольника,
p – полупериметр,

Формулу называют «Формула Брахмагупты»

Четырехугольник	Рисунок	Формула площади	Обозначения
Прямоугольник		S = ab
Параллелограмм
Квадрат		S = a 2
		S = 4r 2
Ромб
Трапеция
		S = m h
Дельтоид		S = ab sin φ
Произвольный выпуклый четырёхугольник
Вписанный четырёхугольник

где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

Формула получается из верхней формулы подстановкой d = 2R

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

Получается из верхней формулы подстановкой d = 2R

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба

где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

где
a и b – основания,
h – высота

φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
r – радиус вписанной окружности

φ – любой из четырёх углов между ними

,

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр

Формулу называют «Формула Брахмагупты»

Прямоугольник
Параллелограмм
Квадрат
	S = a 2 где a – сторона квадрата
	S = 4r 2
Ромб
Трапеция
Дельтоид
	где a и b – неравные стороны, φ1 – угол между сторонами, равными a , φ2 – угол между сторонами, равными b .
Произвольный выпуклый четырёхугольник
Вписанный четырёхугольник

Прямоугольник

где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

Формула получается из верхней формулы подстановкой d = 2R

Параллелограмм

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

Квадрат

где
a – сторона квадрата

Получается из верхней формулы подстановкой d = 2R

Ромб

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба

где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

Трапеция

где
a и b – основания,
h – высота

φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны ,

Дельтоид

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
φ₁ – угол между сторонами, равными a ,
φ₂ – угол между сторонами, равными b .

где
a и b – неравные стороны,
r – радиус вписанной окружности

Произвольный выпуклый четырёхугольник

φ – любой из четырёх углов между ними

Вписанный четырёхугольник

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр

Формулу называют «Формула Брахмагупты»

Вывод формул для площадей четырехугольников

Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле

Доказательство . В соответствии с рисунком 1 справедливо равенство:

что и требовалось доказать.

Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле

где a – сторона параллелограмма, а h_a – высота высота высота , опущенная на эту сторону (рис. 2).

Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому

что и требовалось доказать.

Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле

где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).

то, в силу утверждения 2, справедлива формула

что и требовалось доказать.

Утверждение 4 . Площадь ромба ромба можно найти по формуле

,

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).

что и требовалось доказать.

Утверждение 5 . Площадь трапеции можно найти по формуле

,

где a и b – основания трапеции, а h – высота высота высота (рис.5).

Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому

что и требовалось доказать.

Утверждение 6 . Площадь трапеции трапеции можно найти по формуле

где a и b – основания, а c и d – боковые стороны трапеции ,

(рис.6).

Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

,

что и требовалось доказать.

Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:

где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).

Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.

Если r – радиус вписанной в дельтоид окружности, то

📺 Видео