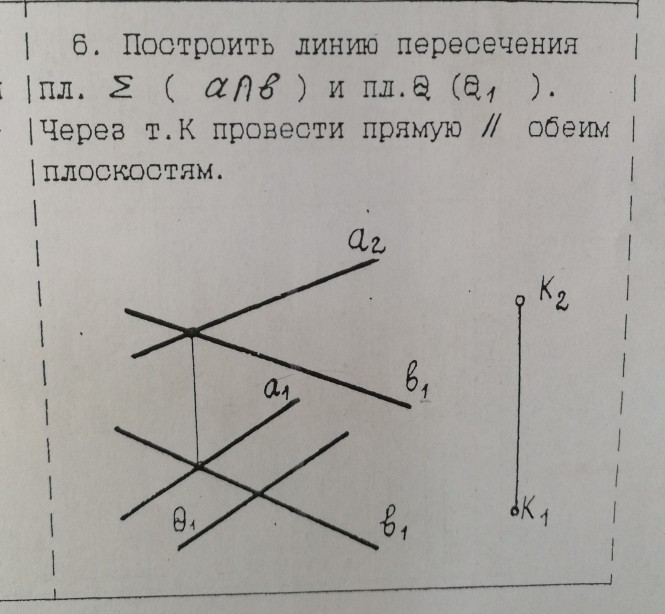
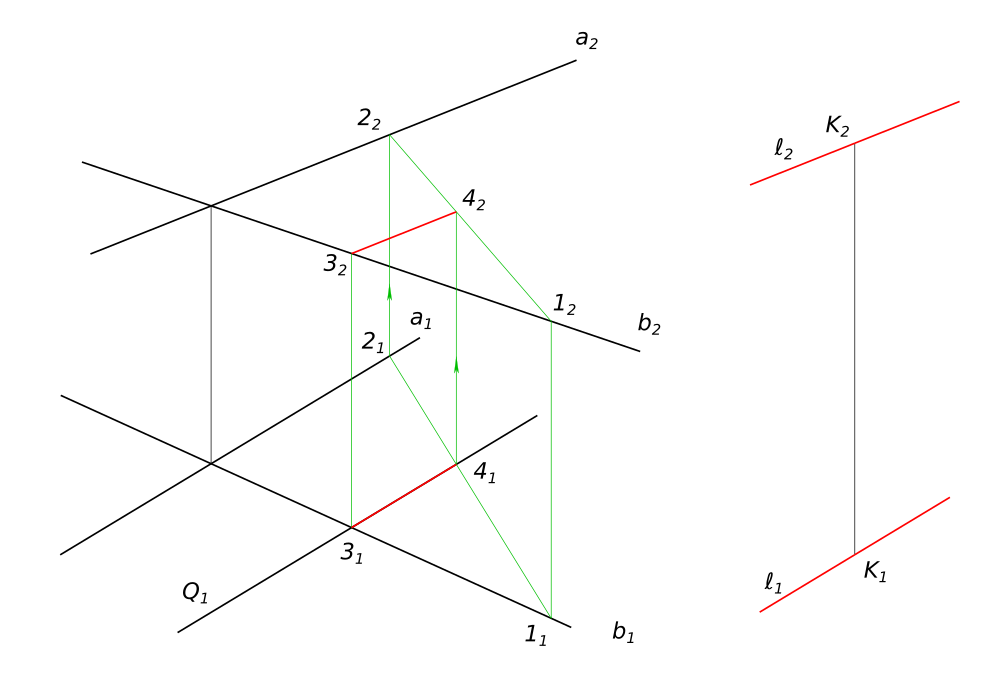
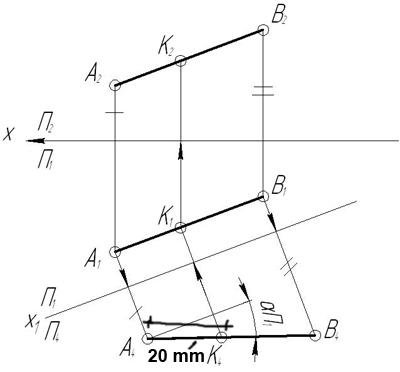
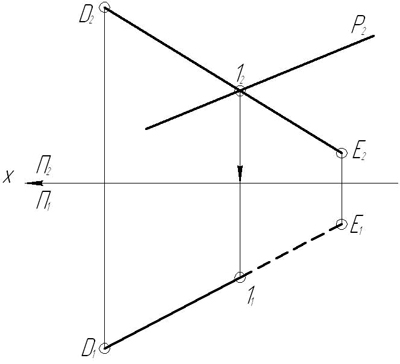
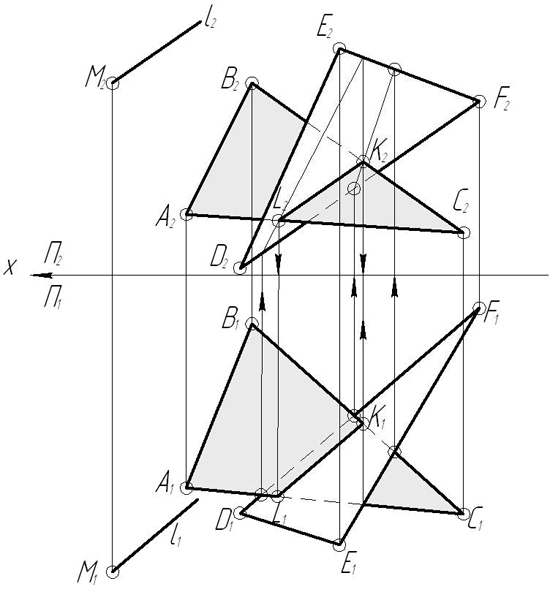
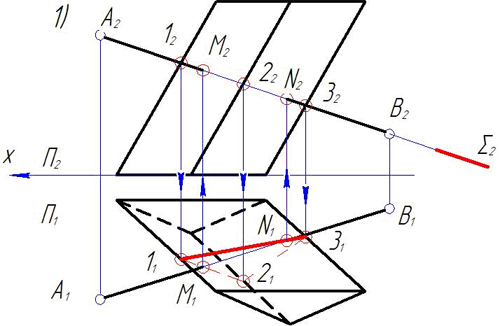
Построить линию пересечения плоскости сигма (a пересекает b) и плоскости Q (Q1). Через точку K провести прямую параллельную обеим плоскостям.
- Комментарии
- Решения задачи
- Построение прямой линии параллельно плоскости
- Начертательная геометрия, решение задач ОмГТУ
- Рабочая тетрадь для решения задач
- Тема 1. Изображение точек на комплексном чертеже.
- Тема 2. Прямая. Взаимное расположение прямых.
- Тема 3. Плоскость. Главные линии плоскости.
- Тема 4. Взаимное расположение прямой и плоскости.
- Тема 5. Взаимное положение плоскостей.
- Тема 7. Пересечение поверхности с плоскостью
- Тема 8. Пересечение прямой линии с поверхностью
- Тема 10. Взаимное пересечение поверхностей.
Комментарии
Решения задачи
Построить линию пересечения плоскости Σ(a ∩ b) и плоскости Q (Q1). Через точку K провести прямую параллельную обеим плоскостям.
Через точку K провести прямую параллельную обеим плоскостям
Используя символьные обозначения для краткости записей геометрических предложений, алгоритма решения задачи, получаем:
Построение прямой линии параллельно плоскости
Построение прямой, параллельной заданной плоскости, основано на следующем положении, известном из геометрии: прямая параллельна плоскости, если эта прямая параллельна любой прямой в плоскости.
Через заданную точку в пространстве можно провести бесчисленное множество прямых линий, параллельных заданной плоскости. Для получения единственного решения требуется какое-нибудь дополнительное условие.
Например, через точку М (рисунок 140) требуется провести прямую, параллельную плоскости, заданной треугольником ЛВС, и плоскости проекций тс! (дополнительное условие).
Очевидно, искомая прямая должна быть параллельна линии пересечения обеих плоскостей, т. е. должна быть параллельна горизонтальному следу плоскости, заданной треугольником АВС. Для определения направления этого следа можно воспользоваться горизонталью плоскости, заданной треугольником АВС. На рисунке 140 проведена горизонталь DC и затем через точку М проведена прямая, параллельная этой горизонтали.
Поставим обратную задачу: например, надо провести плоскость, параллельную прямой CD, через прямую АВ (рисунок 141).
Прямые АВ и CD — скрещивающиеся. Если через одну из двух скрещивающихся прямых требуется провести плоскость, параллельную другой, то задача имеет единственное решение. Через точку В проведена прямая, параллельная прямой CD; прямые АВ и BE определяют плоскость, параллельную прямой CD.
Как установить, параллельна ли данная прямая данной плоскости? Можно попытаться провести в этой плоскости некоторую прямую параллельно данной прямой. Если такую прямую в плоскости не удается построить, то заданные прямая и плоскость не параллельны между собой.
Можно попытаться найти также точку пересечения данной прямой с данной плоскостью. Если такая точка не может быть найдена, то заданные прямая и плоскость взаимно параллельны.
Начертательная геометрия, решение задач ОмГТУ
Рабочая тетрадь для решения задач
по дисциплинe «Начертательная геометрия»
(для студентов заочной формы обучения)
Тема 1. Изображение точек на комплексном чертеже.
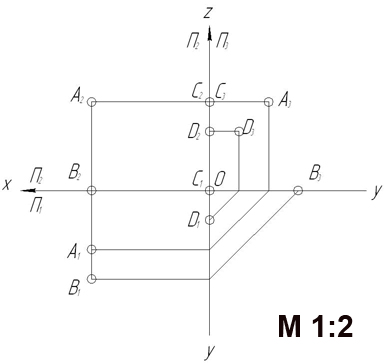
З а д а ч а 1. Построить точки А(40,20,30), В(40,30,0), С(0,0,30) и D(0,10,20) на комплексном чертеже.
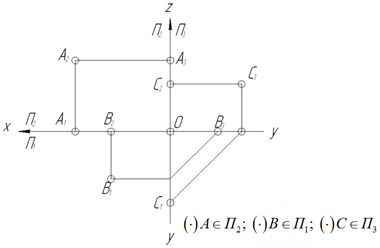
З а д а ч а 2. Точки А, В и С принадлежат плоскостям проекций. Построить недостающие проекции этих точек и указать в какой плоскости каждая из них располагается.
Тема 2. Прямая. Взаимное расположение прямых.
З а д а ч а 3. Даны точки А(90,30,40), В(10,20,15), С(60,20,40) и D(30,40,15). Построить отрезки АВ и СD, обозначить и записать координаты конкурирующих точек.
З а д а ч а 4. Отложить на отрезке АВ отрезок АК=20мм и определить угол наклона отрезка АВ к плоскости проекций П1.
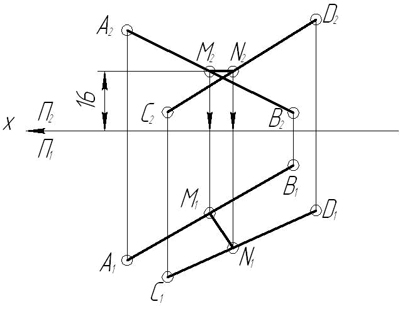
З а д а ч а 5. Пересечь прямые АВ и СD прямой MN, отстоящей от плоскости П1 на расстоянии 16 мм.
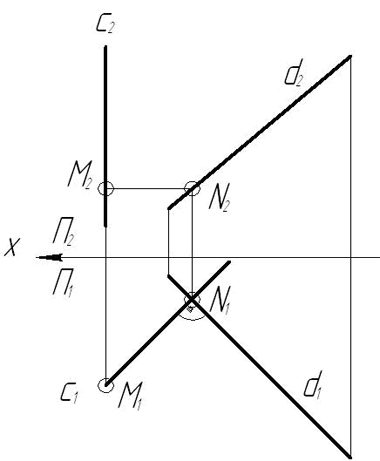
З а д а ч а 6. Даны две скрещивающиеся прямые с и d. Построить отрезок МN, являющийся кратчайшим расстоянием между этими прямыми.
З а д а ч а 7. Дано: точка А(А1,А2) и прямая ВС общего положения. Построить сферу с центром в точке А, касательную к прямой ВС
Тема 3. Плоскость. Главные линии плоскости.
З а д а ч а 8. Дана плоскость сигма (ΔABC), точки D и E в этой плоскости. Через точку Е провести горизонталь h, через точку D – фронталь f этой плоскости.
З а д а ч а 9. Построить недостающие проекции точек E и D, лежащих в плоскости сигма (АВ ∩ ВС).
З а д а ч а 10. Дан плоский пятиугольник ABCDЕ, заданный горизонтальной и фронтальной проекциями двух смежных сторон. Достроить его фронтальную проекцию.
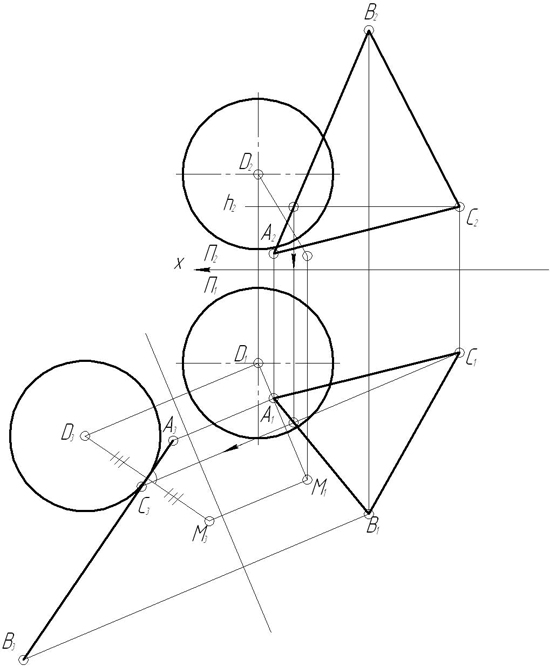
З а д а ч а 11. Дан треугольник АВС. Найти центр окружности, описанной вокруг заданного треугольника.
Тема 4. Взаимное расположение прямой и плоскости.
З а д а ч а 12. Задана плоскость Р и прямая DE. Найти точку пересечения прямой с плоскостью. Определить видимость проекции прямой. (Р2 – фронтальный след плоскости). P (AB//FC).
З а д а ч а 13. Заданы плоскость Р(ΔАВС) и точка D: а) определить расстояние от точки D до плоскости Р; б) построить точку М, симметричную точке D относительно плоскости Р; в) построить шар с центром в точке D, касательный к плоскости Р.
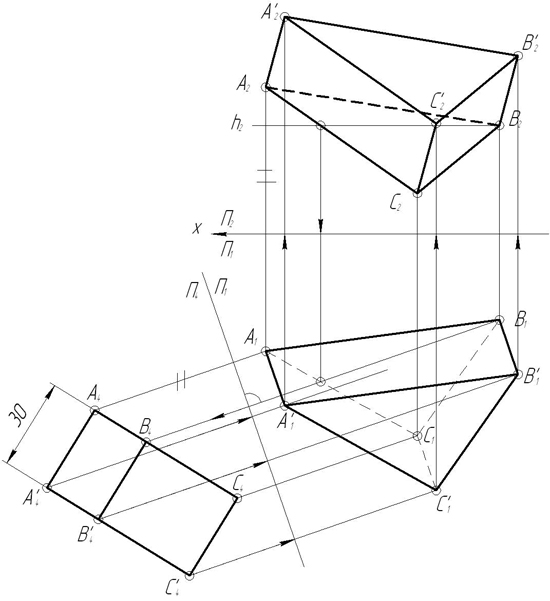
З а д а ч а 14. Задан ΔАВС общего положения. Построить прямую призму с основанием ΔАВС и высотой равной 30 мм.
Тема 5. Взаимное положение плоскостей.
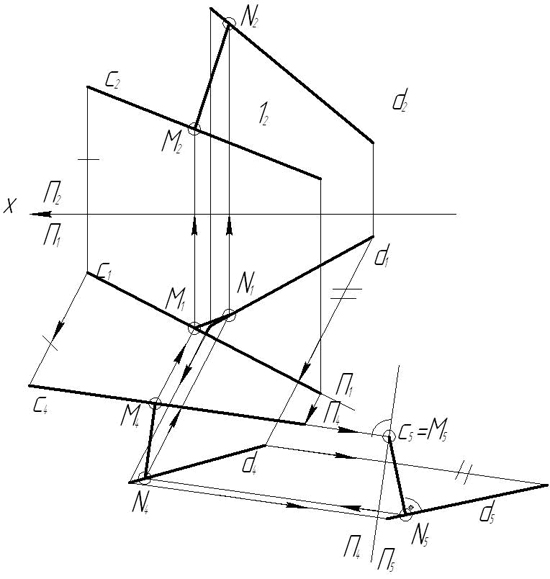
З а д а ч а 15. Даны плоскости сигма(ΔАВС), гамма(DEF) и точка М: а) построить линию пересечения плоскостей. б) через точку М провести прямую l, параллельную плоскостям сигма и гамма. Задачу решить без использования способа замены плоскостей.
З а д а ч а 16 Даны плоскость Р(а//b) и точка М. Через точку М провести плоскость Г, параллельную плоскости Р.
З а д а ч а 17 Даны плоскость Р(а//b) и прямая CD. Через прямую CD провести плоскость Г перпендикул. Р. Г(ΔСDE)
З а д а ч а 18
Тема 7. Пересечение поверхности с плоскостью
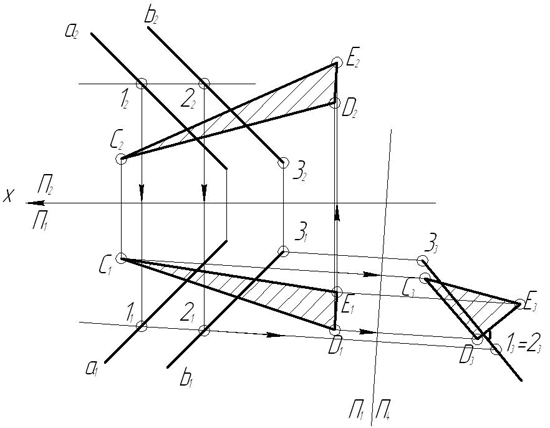
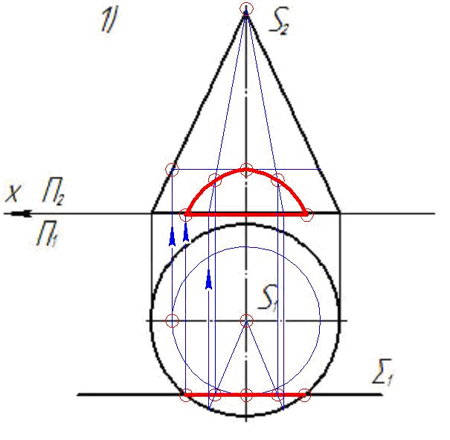
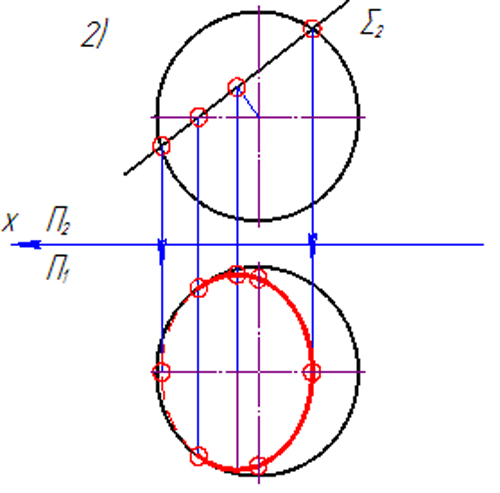
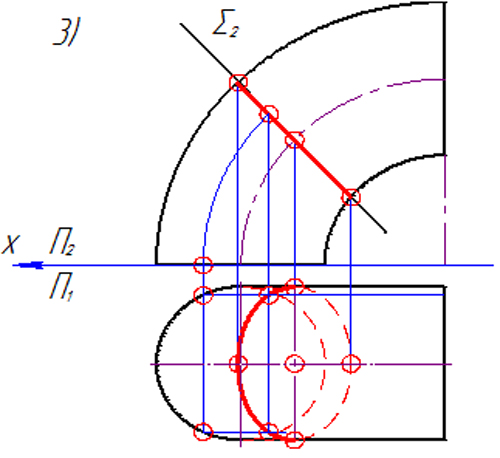
З а д а ч а 19. Построить проекции сечения данной поверхности проецирующей плоскостью Σ.
Тема 8. Пересечение прямой линии с поверхностью
З а д а ч а 20. Построить точки пересечения прямой с заданной поверхностью. Установить видимость проекций прямой
Тема 10. Взаимное пересечение поверхностей.
З а д а ч а 21 Метод вспомогательных секущих плоскостей
З а д а ч а 22 Метод сферического посредника