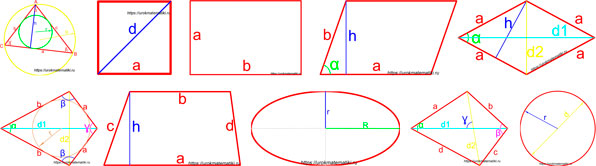
Формулы для площадей четырехугольников Формулы для площадей четырехугольников |
 Вывод формул для площадей четырехугольников Вывод формул для площадей четырехугольников |
 Вывод формулы Брахмагупты для площади вписанного четырехугольника Вывод формулы Брахмагупты для площади вписанного четырехугольника |
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.
- Формулы для площадей четырехугольников
- Вывод формул для площадей четырехугольников
- Тест по геометрии для 8 класса на тему «Четырехугольники»
- «Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Оставьте свой комментарий
- Подарочные сертификаты
- Формулы площадей фигур
- Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
- Формула площади треугольника по трем сторонам
- Формула площади треугольника по двум сторонам и углу между ними
- Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
- Формулы площади квадрата
- Формула площади квадрата по длине стороны
- Формула площади квадрата по длине диагонали
- Формула площади прямоугольника
- Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
- Формула площади параллелограмма по двум сторонам и углу между ними
- Формула площади параллелограмма по двум диагоналям и углу между ними
- Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
- Формула площади ромба по длине стороны и углу
- Формула площади ромба по длинам его диагоналей
- Формулы площади трапеции
- Формула Герона для трапеции
- Формула площади трапеции по длине основ и высоте
- Формулы площади дельтоида
- Формула площади дельтоида по двум неравным сторонам и углу между ними
- Формула площади дельтоида по равным сторонам и углу между ними
- Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности
- Формула площади дельтоида по двум диагоналям
- Формулы площади произвольного выпуклого четырехугольника
- Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними
- Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов
- Формула площади вписанного четырехугольника (формула Брахмагупты)
- Формула площади четырехугольника с вписанной окружностью
- Формула площади четырехугольника с вписанной и описанной окружностями
- Формулы площади круга
- Формула площади круга через радиус
- Формула площади круга через диаметр
- Площадь сегмента круга
- Площадь кругового сегмента через угол в градусах.
- Площадь кругового сегмента через угол в радианах.
- Формула площади эллипса
- 🔥 Видео
Видео:Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать

Формулы для площадей четырехугольников
| Четырехугольник | Рисунок | Формула площади | Обозначения | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прямоугольник |  | S = ab | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Параллелограмм |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
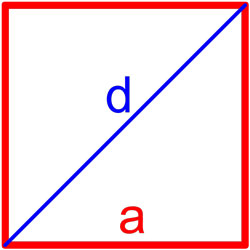
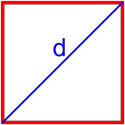
| Квадрат |  | S = a 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | S = 4r 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ромб |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Трапеция |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | S = m h | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дельтоид |  | S = ab sin φ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Произвольный выпуклый четырёхугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вписанный четырёхугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прямоугольник | ||
 | ||
 | ||
 | ||
| Параллелограмм | ||
 | ||
 | ||
 | ||
| Квадрат | ||
 | S = a 2 где | |
 | S = 4r 2 | |
 | ||
 | ||
| Ромб | ||
 | ||
 | ||
 | ||
 | ||
 | ||
| Трапеция | ||
 | ||
 | ||
 | ||
 | ||
| Дельтоид | ||
 | ||
 |  где | |
 | ||
 | ||
| Произвольный выпуклый четырёхугольник | ||
 | ||
| Вписанный четырёхугольник | ||
 | ||
| Прямоугольник |
 |
где
a и b – смежные стороны

где
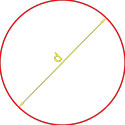
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R

где
a – сторона,
ha – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

где
a – сторона квадрата



Получается из верхней формулы подстановкой d = 2R

где
a – сторона,
ha – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба



где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

где
a и b – основания,
h – высота


φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны ,

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .

где
a и b – неравные стороны,
r – радиус вписанной окружности


φ – любой из четырёх углов между ними

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
Видео:Площадь прямоугольника. Как найти площадь прямоугольника?Скачать

Вывод формул для площадей четырехугольников
Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле
Доказательство . В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле
где a – сторона параллелограмма, а ha – высота высота высота , опущенная на эту сторону (рис. 2).
Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
что и требовалось доказать.
Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
то, в силу утверждения 2, справедлива формула
что и требовалось доказать.
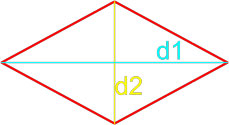
Утверждение 4 . Площадь ромба ромба можно найти по формуле

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
что и требовалось доказать.
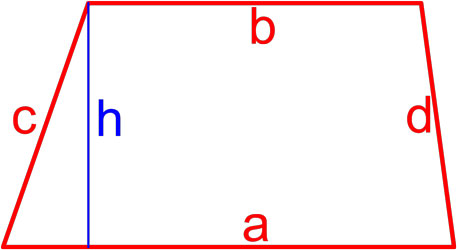
Утверждение 5 . Площадь трапеции можно найти по формуле

где a и b – основания трапеции, а h – высота высота высота (рис.5).
Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому
что и требовалось доказать.
Утверждение 6 . Площадь трапеции трапеции можно найти по формуле
где a и b – основания, а c и d – боковые стороны трапеции ,
(рис.6).
Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

что и требовалось доказать.
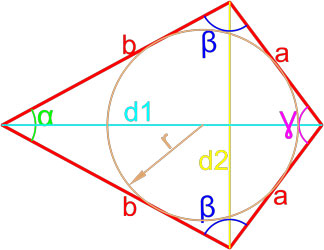
Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Тест по геометрии для 8 класса на тему «Четырехугольники»
Видео:Геометрия 8. Урок 13 - Площадь четырехугольников. ЗадачиСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
1.Любой прямоугольник является:
а) ромбом; б) квадратом;
в)параллелограммом; г) нет правильного ответа.
2. Если в четырехугольнике диагонали перпендикулярны, то этот четырехугольник — .
а) ромб; б) квадрат;
в)параллелограмм; г) нет правильного ответа.
3. Ромб – это четырехугольник, в котором …
а)диагонали точкой пересечения делятся пополам и равны;
б) диагонали взаимно перпендикулярны и точкой пересечения делятся пополам;
в) противолежащие стороны параллельны, а противолежащие углы равны;
г) нет правильного ответа.
1. Любой ромб является :
а) квадратом; б) прямоугольником;
в) параллелограммом; г) нет правильного ответа.
2.Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм- … .
а) ромб; б) квадрат;
в)прямоугольник; г) нет правильного ответа.
3.Прямоугольник — это четырехугольник, в котором:
а) противолежащие стороны параллельны, а диагонали равны;
б) диагонали точкой пересечения делятся пополам и являются биссектрисами его углов;
в)два угла прямые и две стороны равны;
г) нет правильного ответа.
1.Любой прямоугольник является:
а) ромбом; б) квадратом;
в)параллелограммом; г) нет правильного ответа.
2. Если в четырехугольнике диагонали перпендикулярны, то этот четырехугольник — .
а) ромб; б) квадрат;
в)параллелограмм; г) нет правильного ответа.
3. Ромб – это четырехугольник, в котором …
а)диагонали точкой пересечения делятся пополам и равны;
б) диагонали взаимно перпендикулярны и точкой пересечения делятся пополам;
в) противолежащие стороны параллельны, а противолежащие углы равны;
г) нет правильного ответа.
1. Любой ромб является :
а) квадратом; б) прямоугольником;
в) параллелограммом; г) нет правильного ответа.
2.Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм- … .
а) ромб; б) квадрат;
в)прямоугольник; г) нет правильного ответа.
3.Прямоугольник — это четырехугольник, в котором:
а) противолежащие стороны параллельны, а диагонали равны;
б) диагонали точкой пересечения делятся пополам и являются биссектрисами его углов;
в)два угла прямые и две стороны равны;
г) нет правильного ответа.
1 вариант 1 в); 2 г); 3 б)
Видео:Площади четырехугольников: трапеция, параллелограмм, ромб. Геометрия на клеточке. ОГЭСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 975 человек из 79 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 697 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 334 человека из 71 региона
Ищем педагогов в команду «Инфоурок»
- Меркулова Татьяна ВячеславовнаНаписать 8557 29.10.2015
Номер материала: ДВ-108209
- 29.10.2015 528
- 29.10.2015 8047
- 29.10.2015 7285
- 29.10.2015 5330
- 29.10.2015 2205
- 29.10.2015 2068
- 29.10.2015 543
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Минпросвещения готовит рекомендации по построению «идеальной школы»
Время чтения: 1 минута
В Госдуме предложили продлить каникулы для школьников до 16 января
Время чтения: 1 минута
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:8 класс, 12 урок, Площадь прямоугольникаСкачать

Формулы площадей фигур
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Видео:Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Формулы площади треугольника
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
где a — одна из сторон треугольника, h — высота, проведенная к стороне треугольника.
Формула площади треугольника по трем сторонам
Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .
S = p p — a p — b p — c ,
где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 1 2 a · b · sin γ ,
где a, b — стороны треугольника,
γ — угол между сторонами a и b .
Формула площади треугольника по трем сторонам и радиусу описанной окружности
a, b, c — стороны треугольника,
R — радиус описанной окружности.
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
где S — площадь треугольника,
r — радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c 2
Видео:ОГЭ по математике. Площадь четырехугольника можно вычислить по формуле (вар. 5)Скачать

Формулы площади квадрата
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
где S — площадь квадрата,
a — длина стороны квадрата.
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.
где S — площадь квадрата,
d — длина диагонали квадрата.
Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон.
где S — площадь прямоугольника,
a, b — длины сторон прямоугольника.
Видео:Урок 8. Вычисление площадей треугольнико четырехугольников. Площадь круга | МатематикаСкачать

Формулы площади параллелограмма
Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны.
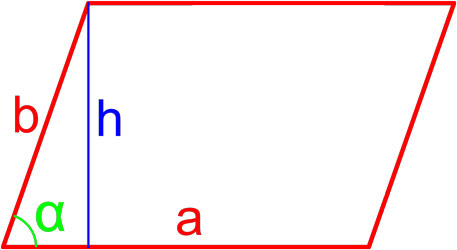
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
где S — площадь параллелограмма,
a, h — длины сторон параллелограмма.
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
где S — площадь параллелограмма,
a, b — длины сторон параллелограмма,
α — угол между сторонами параллелограмма.
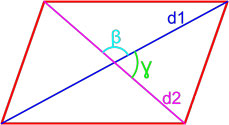
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.
S = d1 · d2 · sin β 2 = d1 · d2 · sin γ 2 ,
где S — площадь параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
β , γ — угол между диагоналями параллелограмма.
Видео:ОГЭ по математике. Площадь четырехугольника можно вычислить (вар. 4)Скачать

Формулы площади ромба
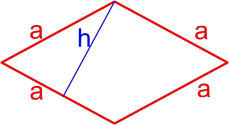
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
где S — площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба.
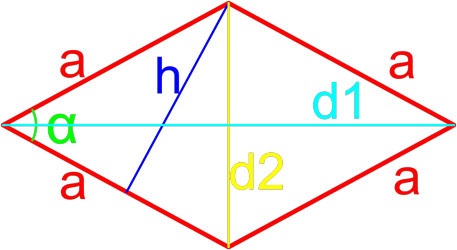
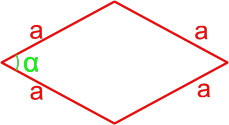
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
где S — площадь ромба,
a — длина стороны ромба,
α — угол между сторонами ромба.
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
где S — площадь ромба,
d1, d2 — длины диагоналей ромба.
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Формулы площади трапеции
Трапеция — это четырёхугольник, у которого две ( a, b ) стороны параллельны (основания), а две другие ( c, d ) стороны не параллельны (боковые стороны).
Формула Герона для трапеции
где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,
p = a + b + c + d 2 — полупериметр трапеции.
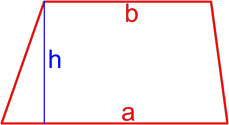
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы её оснований на высоту.
где S — площадь трапеции,
a, b — длины основ трапеции,
h — высота трапеции.
Видео:Площадь круга. Математика 6 класс.Скачать

Формулы площади дельтоида
Дельтоид — это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания.
Формула площади дельтоида по двум неравным сторонам и углу между ними
Площадь дельтоида равна произведению длин неравных сторон на синус угла между ними.
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
β — угол между неравными сторонами дельтоида.
Формула площади дельтоида по равным сторонам и углу между ними
Площадь дельтоида равна полусумме произведения каждой из пар равных сторон на синус угла между ними.
S = a 2 sin γ + b 2 sin α 2 ,
где S — площадь дельтоида,
a, b — длины сторон дельтоида,
α — угол между равными сторонами b ,
γ — угол между равными сторонами a .
Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности
Площадь дельтоида равна произведению суммы неравных сторон на радиус вписанной окружности.
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
r — радиус вписанной окружности.
Формула площади дельтоида по двум диагоналям
Площадь дельтоида равна половине произведения длин двух диагоналей.
где S — площадь дельтоида,
d1, d2 — диагонали дельтоида.
Видео:8 класс, 13 урок, Площадь параллелограммаСкачать

Формулы площади произвольного выпуклого четырехугольника
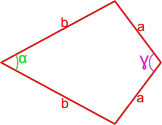
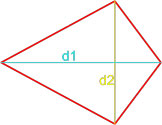
Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними
Площадь произвольного выпуклого выпуклого четырехугольника равна половине произведения его диагоналей умноженной на синус угла между ними.
S = d1 · d2 · sin γ 2 ,
где S — площадь четырехугольника,
d1, d2 — диагонали четырехугольника,
γ — любой из четырёх углов между диагоналями.
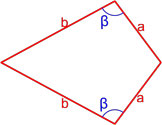
Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника,
θ = α + β 2 — полусумма двух противоположных углов четырехугольника.
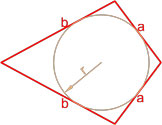
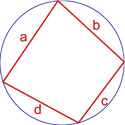
Формула площади вписанного четырехугольника (формула Брахмагупты)
Если вокруг четырехугольника можно описать окружность, то его площадь равна
S = p — a p — b p — c p — d ,
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника.
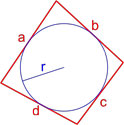
Формула площади четырехугольника с вписанной окружностью
Если в четырехугольник можно вписать окружность, то его площадь равна:
где S — площадь четырехугольника,
r — радиус вписанной окружности,
p = a + b + c + d 2 — полупериметр четырехугольника.
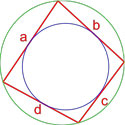
Формула площади четырехугольника с вписанной и описанной окружностями
Если в четырехугольник можно вписать окружность, а также около него можно описать окружность, то его площадь равна:
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника.
Видео:Задание 3 ЕГЭ по математике. Урок 11Скачать

Формулы площади круга
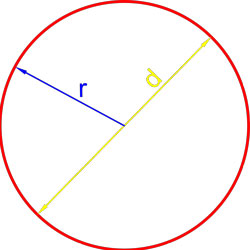
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.
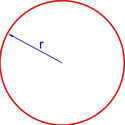
где S — площадь круга,
r — радиус круга.
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.
где S — площадь круга,
d — диаметр круга.
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Площадь сегмента круга
Площадь кругового сегмента через угол в градусах.
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в градусах.
Площадь кругового сегмента через угол в радианах.
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в радианах.
Видео:Задача В8 № 27610 ЕГЭ-2015 по математике. Урок 60Скачать

Формула площади эллипса
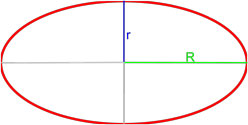
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
где S — площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.
🔥 Видео
Лучший способ найти площадь кругаСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

ОГЭ/База Все прототипы задач на четырехугольникиСкачать






 ,
,