Собственный вектор геометрический смысл (7 видео)

Собственные векторы и значения линейного оператора (преобразования)

Пусть — линейное преобразование n-мерного линейного пространства . Ненулевой вектор линейного пространства , удовлетворяющий условию

называется собственным вектором линейного преобразования . Число в равенстве (9.5) называется собственным значением преобразования . Говорят, что собственный вектор соответствует (принадлежит) собственному значению . Если пространство вещественное (комплексное), то собственное значение — действительное (комплексное) число.

Множество всех собственных значений линейного преобразования называется его спектром .

Поясним геометрический смысл собственных векторов. Ненулевой вектор s является собственным для преобразования , если его образ коллинеарен прообразу . Другими словами, если — собственный вектор, то преобразование имеет одномерное инвариантное подпространство . Справедливо и обратное утверждение.

В самом деле, пусть собственный вектор соответствует некоторому собственному значению . Любой вектор из имеет вид , где — любое число из заданного поля. Найдем образ этого вектора

Следовательно, для любого вектора , т.е. подпространство инвариантно относительно преобразования . Размерность подпространства равна единице, так как по определению.

Обратное утверждение доказывается, проводя рассуждения в обратном порядке.

Содержание

Связь собственных векторов линейного преобразования (оператора) и его матрицы
Нахождение собственных векторов и значений линейного оператора (преобразования)
Примеры собственных векторов линейных операторов (преобразований)
Собственные значения и собственные векторы
📺 Видео

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Связь собственных векторов линейного преобразования (оператора) и его матрицы

Ранее рассматривались собственные векторы и собственные значения матрицы. Напомним, что собственным вектором квадратной матрицы n-го порядка называется ненулевой числовой столбец , удовлетворяющий условию (7.13):

Число в (9.6) называется собственным значением матрицы . При этом считалось, что собственное значение и числа принадлежат полю комплексных чисел.

Эти понятия связаны с собственными векторами и собственными значениями линейного преобразования.

Теорема 9.3 о собственных векторах линейного преобразования и его матрицы. Пусть — линейное преобразование n-мерного линейного пространства с базисом . Тогда собственное значение и координатный столбец собственного вектора преобразования являются собственным значением и собственным вектором матрицы этого преобразования, определенной относительно базиса , т.е.

Обратное утверждение справедливо при дополнительных условиях: если столбец и число являются собственным вектором и собственным значением матрицы , причем числа принадлежат тому же числовому полю, над которым определено линейное пространство , то вектор и число являются собственным вектором и собственным значением линейного преобразования с матрицей в базисе .

В самом деле, условие (9.5) в координатной форме имеет вид (9.6), что совпадает с определением (7.13) собственного вектора матрицы. Наоборот, из равенства (9.6) следует равенство (9.5) при условии, что векторы и определены, т.е. числа принадлежат тому же числовому полю, над которым определено линейное пространство.

Напомним, что нахождение собственных значений матрицы сводится к решению ее характеристического уравнения , где — характеристический многочлен матрицы . Для линейного преобразования введем аналогичные понятия.

Характеристическим многочленом линейного преобразования n-мерного линейного пространства называется характеристический многочлен матрицы этого преобразования, найденной относительно любого базиса пространства .

Уравнение называется характеристическим уравнением линейного преобразования .

Преобразование называется характеристическим для линейного преобразования .

1. Характеристический многочлен линейного преобразования не зависит от базиса, в котором найдена матрица преобразования.

В самом деле, матрицы и линейного преобразования в базисах и являются, согласно (9.4), подобными: , где — матрица перехода от базиса к базису . Как показано ранее, характеристические многочлены подобных матриц совпадают (см. свойство 3). Поэтому для характеристического многочлена преобразования можно использовать обозначение , не указывая матрицу этого преобразования.

2. Из теоремы 9.3 следует, что любой комплексный (действительный, рациональный) корень характеристического уравнения является собственным значением линейного преобразования линейного пространства , определенного над полем комплексных (действительных, рациональных) чисел.

3. Из теоремы 9.3 следует, что любое линейное преобразование комплексного линейного пространства имеет одномерное инвариантное подпространство, так как это преобразование имеет собственное значение (см. пункт 2), а следовательно, и собственные векторы. Таким подпространством является, например, линейная оболочка любого собственного вектора. У преобразования вещественного линейного пространства одномерных инвариантных подпространств может и не быть, если все корни характеристического уравнения комплексные (но не действительные).

Теорема 9.4 об инвариантных подпространствах линейного оператора вещественного пространства. У всякого линейного преобразования вещественного линейного пространства существует одномерное или двумерное инвариантное подпространство.

Действительно, составим матрицу линейного преобразования n-мерного вещественного линейного пространства в произвольном базисе . Элементы этой матрицы — действительные числа. Следовательно, характеристический многочлен — это многочлен степени с действительными коэффициентами. Согласно следствиям 3, 4 основной теоремы алгебры, такой многочлен может иметь действительные корни и пары комплексных сопряженных корней.

Если — действительный корень характеристического уравнения, то и соответствующий собственный вектор матрицы также действительный. Поэтому он определяет собственный вектор линейного преобразования (см. теорему 9.3). В этом случае существует одномерное инвариантное относительно подпространство (см. геометрический смысл собственных векторов).

Если — пара комплексных сопряженных корней , то собственный вектор матрицы также с комплексными элементами: . Его можно представить в виде , где — действительные столбцы. Равенство (9.6) при этом будет иметь вид

Выделяя действительную и мнимую части, получаем систему

Покажем, что столбцы и линейно независимы. Рассмотрим два случая. Если , то из первого уравнения (9.7) следует, что , так как . Тогда , что противоречит условию . Предположим, что и столбцы и пропорциональны, т.е. существует такое действительное число , что . Тогда из системы (9.7) получаем Прибавляя ко второму уравнению первое, умноженное на , приходим к равенству . Так как , то выражение в квадратных скобках равно нулю, т.е. . Поскольку , то . Этого не может быть, так как — действительное число. Получили противоречие. Таким образом, столбцы и линейно независимы.

Рассмотрим подпространство , где . Это подпространство двумерное, так как векторы линейно независимы (как показано выше, их координатные столбцы линейно независимы). Из (9.7) следует, что т.е. образ любого вектора, принадлежащего , также принадлежит . Следовательно, — двумерное подпространство, инвариантное относительно преобразования , что и требовалось доказать.

Видео:Собственные векторы и собственные значенияСкачать

Нахождение собственных векторов и значений линейного оператора (преобразования)

Для нахождения собственных векторов и собственных значений линейного преобразования вещественного линейного пространства следует выполнить следующие действия.

1. Выбрать произвольный базис линейного пространства и найти в этом базисе матрицу преобразования .

2. Составить характеристический многочлен преобразования .

3. Найти все различные действительные корни характеристического уравнения . Комплексные (но не действительные) корни характеристического уравнения следует отбросить (см. пункт 2. замечаний 9.4).

4. Для корня найти фундаментальную систему решений однородной системы уравнений , где . Для этого можно использовать либо алгоритм решения однородной системы, либо один из способов нахождения фундаментальной матрицы.

5. Записать линейно независимые собственные векторы преобразования , отвечающие собственному значению

Для нахождения совокупности всех собственных векторов, отвечающих собственному значению , образовать ненулевые линейные комбинации

где — произвольные постоянные, не равные нулю одновременно.

Повторить пункты 4, 5 для остальных собственных значений линейного преобразования .

Для нахождения собственных векторов линейного преобразования комплексного линейного пространства нужно в пункте 3 определить все корни характеристического уравнения и, не отбрасывая комплексные корни, выполнить для них пункты 4,5.

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

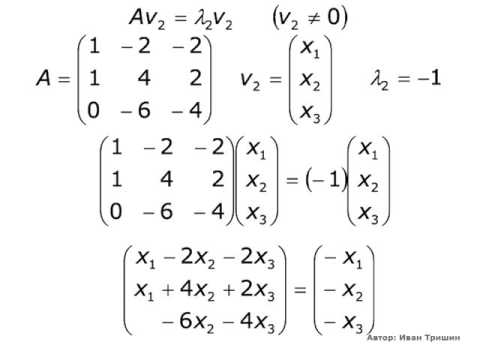
Примеры собственных векторов линейных операторов (преобразований)

1. Для нулевого преобразования любой ненулевой вектор является собственным, соответствующим нулевому собственному значению , так как .

2. Для тождественного преобразования любой ненулевой вектор является собственным, соответствующим единичному собственному значению , так как .

3. Для центральной симметрии любой ненулевой вектор является собственным, соответствующим собственному значению , так как .

4. Для гомотетии любой ненулевой вектор является собственным, соответствующим собственному значению (коэффициенту гомотетии), так как .

5. Для поворота плоскости (при ) собственных векторов нет, так как при повороте на угол, не кратный , образ каждого ненулевого вектора неколлинеарен прообразу. Здесь рассматривается поворот вещественной плоскости, т.е. двумерного векторного пространства над полем действительных чисел.

6. Для оператора дифференцирования любой ненулевой многочлен нулевой степени (не равный тождественно нулю) является собственным вектором, соответствующим нулевому собственному значению , так как . Любой многочлен ненулевой степени не является собственным вектором, так как многочлен не пропорционален своей производной: , поскольку они имеют разные степени.

7. Рассмотрим оператор проектирования на подпространство параллельно подпространству . Здесь для . Для этого оператора любой ненулевой вектор является собственным, соответствующим собственному значению , так как , а любой ненулевой вектор является собственным, соответствующим собственному значению , так как . Другие векторы не являются собственными, так как равенство возможно либо при , либо при .

8. Рассмотрим оператор отражения на подпространство параллельно подпространству . Здесь , для . Для этого оператора любой ненулевой вектор является собственным, соответствующим собственному значению , так как , а любой ненулевой вектор является собственным, соответствующим собственному значению , так как . Другие векторы не являются собственными, так как равенство возможно либо при , либо при .

9. В пространстве радиус-векторов пространства, отложенных от фиксированной точки , рассмотрим поворот на угол , вокруг оси , заданной радиус-вектором . Любой ненулевой вектор, коллинеарный вектору , является собственным, отвечающим собственному значению . Других собственных векторов у этого преобразования нет.

Пример 9.1. Найти собственные значения и собственные векторы оператора дифференцирования , преобразующего пространство тригонометрических многочленов (частоты ):

а) с действительными коэффициентами ;

б) с комплексными коэффициентами .

Решение. 1. Выберем стандартный базис и составим в этом базисе матрицу оператора

2. Составим характеристический многочлен преобразования .

3. Характеристическое уравнение имеет комплексные сопряженные корни . Действительных корней нет, поэтому преобразование вещественного пространства (случай (а)) не имеет собственных значений, а следовательно, и собственных векторов. Преобразование комплексного пространства (случай (б)) имеет комплексные собственные значения .

4(1). Для корня находим фундаментальную систему решений однородной системы уравнений

Приведем матрицу системы к ступенчатому виду, умножая первое уравнение на и вычитая его из второго уравнения:

Выражаем базисную переменную через свободную: . Полагая , получаем , т.е. .

5(1). Записываем собственный вектор, отвечающий собственному значению . Совокупность всех собственных векторов, отвечающих собственному значению , образуют ненулевые функции, пропорциональные .

4(2). Для корня аналогично находим фундаментальную систему (состоящую из одного вектора) решений однородной системы уравнений

5(2). Записываем собственный вектор, отвечающий собственному значению . Совокупность всех собственных векторов, отвечающих собственному значению , образуют ненулевые функции, пропорциональные .

Видео:Собственные векторы и собственные значения матрицыСкачать

Собственные значения и собственные векторы

Пусть /д(А) = det (4 — XI) — характеристический многочлен матрицы А порядка п над полем Р. Предположим, что он имеет корень, принадлежащий полю Р. Обозначим этот корень той же буквой Л, т. е. далее полагаем, что Л — это число из поля Р. Поскольку det (4 — XI) = 0, однородное уравнение (4 — Х1)х = О имеет нетривиальное решение х G Р» и, следовательно,

Соотношение (*) можно рассматривать и без какой-либо связи с характеристическим многочленом. Более того, оно имеет смысл, если считать, что 4 — некоторый линейный оператор на каком-то пространстве V над полем Р, х G V и А е Р. Число Л и вектор х 0, связанные соотношением (*), называются собственным значением и собственным вектором матрицы или оператора 4.

Связь собственных значений и корней характеристического многочлена описывается следующим, в действительности уже полученным нами, утверждением.

Утверждение 5.5.1. Собственные значения линейного оператора на конечномерном пространстве и только они являются корнями его характеристического многочлена.

Обратим внимание на ясный геометрический смысл собственного вектора: при действии на него оператором 4 он просто умножается на соответствующее ему собственное значение.

Если в пространстве V имеется базис из собственных векторов оператора, то в этом базисе данный оператор представляется, очевидно, диагональной матрицей. Такой оператор называется оператором простой структуры или диагонализуемым оператором.

Простым достаточным условием диагонализуемости является простота собственных значений и предположение о том, что поле разложения характеристического многочлена содержится в поле Р. Собственное значение называется простым, если оно является простым корнем характеристического многочлена. В противном случае собственное значение называется кратным. Говорят, что собственное значение имеет алгебраическую кратность к, если для характеристического многочлена оно является корнем кратности к. Упомянутое выше условие диагонализуемости вытекает из следующей теоремы.

Теорема 5.5.1. Если собственные векторы х. Хк линейного оператора А соответствуют попарно различным собственным значениям Х. Хк, т о они линейно независимы.

Доказательство. Рассмотрим равную нулю линейную комбинацию данных собственных векторов и подействуем на нее оператором А:

Из последнего равенства вычтем равенство

хь (IZaiXi)= 0 52

Далее очевидным образом применяется индукция по к. ?

Пусть Л — собственное значение линейного оператора А: V V. Множество L всех векторов х eV, таких что Ах = Хх, называется собственным подпространством оператора А, отвечающим данному собственному значению Л. То, что L будет подпространством в V, проверяется тривиальным образом. Каждый ненулевой вектор из L является собственным вектором для Л, и очевидно, что L содержит все собственные векторы, соответствующие Л. Размерность пространства L называется геометрической кратностью собственного значения Л.

Утверждение 5.5.2. Геометрическая кратность собственного значения меньше или равна его алгебраической кратности.

Доказательство. Пусть линейный оператор А действует в n-мерном пространстве V над полем Р, и пусть Л1 — его собственное значение геометрической кратности I. Выберем базис е. ,е_п пространства V таким образом, чтобы векторы е. ,е/ составили базис собственного подпространства для Ль В этом базисе матрица оператора А примет вид

И]е =

Поэтому характеристический многочлен представляет собой произведение

det (411 — AZ/) det (4₂2 — = (Ai — A) z det (Д₂₂ — AZ_n_/).

Отсюда видно, что l не может быть больше алгебраической кратности корня Ль ?

Вопрос о существовании собственных значений, а значит и собственных подпространств, — это вопрос о том, имеет ли характеристический многочлен корни в поле Р. Мы уже знаем, впрочем, что всегда можно перейти к более широкому полю разложения характеристического многочлена, в котором он будет иметь п корней с учетом кратностей. Довольно естественным образом исходное n-мерное пространство V можно сделать подмножеством нового n-мерного пространства над этим более широким полем и доопределить действие оператора на новом пространстве.

Задача 208. Пусть А — матрица порядка п и ранга г. Докажите, что матрица I А А имеет собственное значение 1 алгебраической кратности не меньше п — г.

Задача 209. Матрица А = [а^] порядка п имеет верхний почти треугольный вид, т.е. aij = 0 при i > j + 1. Кроме того, ai₊,i 0 при 1 г п — 1. Докажите, что если матрица А диагонализуема, то она имеет п попарно различных собственных значений.

Задача 210. Докажите, что диагонализуемая матрица ранга г обладает ненулевым главным минором порядка г.

Задача 211. Комплексная матрица А порядка п обратима, совпадает со своей сопряженной матрицей и известно, что окаймляющая ее матрица

также является обратимой.

[ В обратима и матрица

Докажите, что матрица

д-1

имеет собственные значения 1 и (1 ± х/5)/2 алгебраической кратности п — г и г соответственно.

Задача 212. Пусть Л — собственное значение матрицы А е С пхп . Докажите, что

Задача 213. Все элементы матрицы А е IR nxn неотрицательны, а суммы элементов в каждой строке одинаковы и равны Л. Докажите, что Л является наибольшим по модулю собственным значением матрицы А.

Задача 214. Придумайте, как найти алгебраические кратности собственных значений комплексной матрицы, не вычисляя сами собственные значения. Докажите, что это можно сделать за конечное число арифметических операций.