Правильная пятиугольная призма вписанная в окружность (7 видео)

Как нарисовать пятиугольную призму? Объем и площадь поверхности фигуры

Пятиугольная призма при решении задач по геометрии встречается гораздо реже, чем такие призмы, как треугольная, четырехугольная или шестиугольная. Тем не менее полезно рассмотреть основные свойства этой фигуры, а также узнать, как ее можно нарисовать.

Содержание

Что собой представляет пятиугольная призма?
Элементы призмы
Как начертить пятиугольную призму?
Площадь фигуры
Объем фигуры
Правильная пятиугольная призма
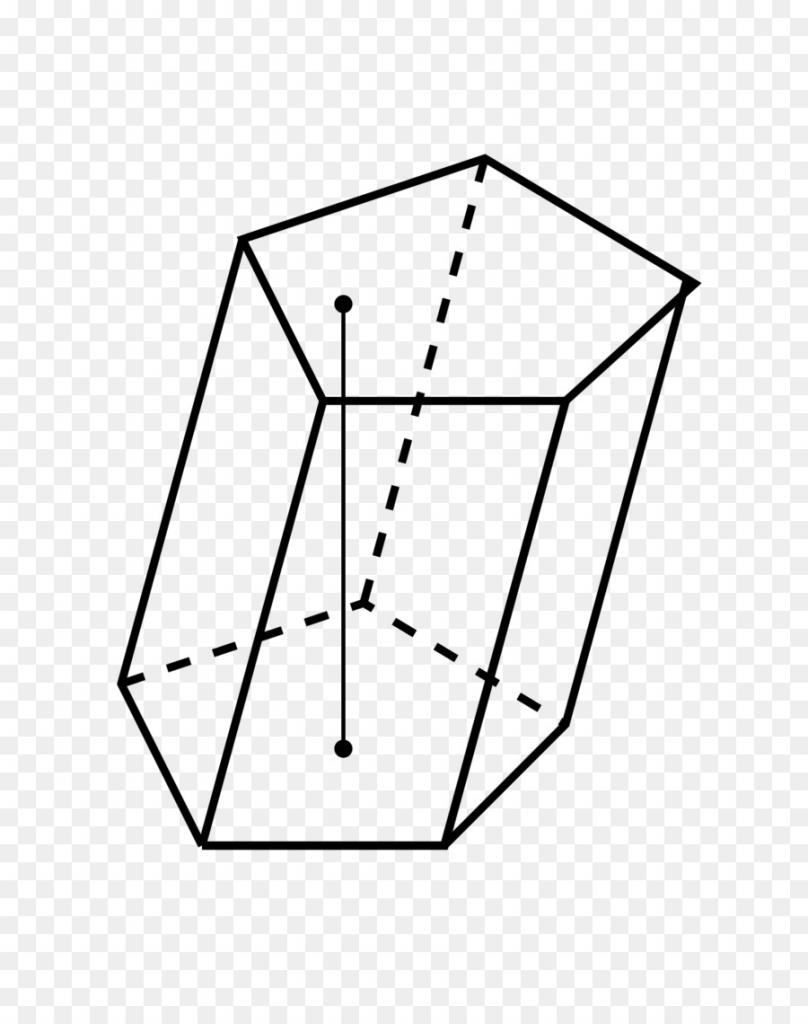
Пятиугольная призма — это многогранник, две грани которого являются равными пятиугольниками, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими пятиугольниками.
ЗАДАНИЕ 9 «ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ»
💥 Видео

Видео:Как построить шестиугольник вписанный в окружностьСкачать

Что собой представляет пятиугольная призма?

Речь идет об объемной фигуре, основания которой являются пятиугольниками, а боковые стороны — параллелограммами. Если каждый из этих параллелограммов будет перпендикулярен параллельным основаниям, то такая призма называется прямоугольной. Боковая поверхность прямоугольной пятиугольной призмы составлена из пяти прямоугольников. Причем прилегающая к основанию сторона каждого из них равна соответствующей длине стороны пятиугольника.

Если пятиугольник будет правильным, то есть все его стороны и углы будут равны друг другу, тогда такая прямоугольная призма называется правильной. Далее в статье будем рассматривать свойства именно этой фигуры.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Элементы призмы

Для нее, как и для любой призмы, характерны следующие элементы:

грани или стороны — это части плоскостей, ограничивающих фигуру в пространстве;
вершины — точки пересечения трех сторон;
ребра — отрезки пересечения двух сторон фигуры.

Числа всех названных элементов связаны друг с другом следующим равенством:

Число ребер = число вершин + число граней — 2

Это выражение носит название формулы Эйлера для полиэдра.

В пятиугольной призме количество сторон равно семи (два основания + пять прямоугольников). Число вершин составляет 10 (по пять для каждого основания). Число ребер в таком случае будет равно:

Десять ребер принадлежат основаниям призмы, а пять ребер образованы прямоугольниками.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Как начертить пятиугольную призму?

Ответ на этот вопрос зависит от конкретной задачи. Если необходимо начертить произвольную призму, тогда следует изобразить любой пятиугольник. После этого провести пять параллельных отрезков равной длины из каждой вершины пятиугольника. Затем, соединить верхние концы отрезков. Получилась пятиугольная произвольная призма.

Если же следует начертить правильную призму, тогда вся сложность задачи сводится к получению правильного пятиугольника. Существует несколько способов начертить этот многоугольник. Здесь мы рассмотрим только два способа.

Первый способ заключается в построении окружности с помощью циркуля. Затем проводится произвольный диаметр окружности и от него отсчитывается с помощью транспортира пять углов по 72 o (5*72 o = 360 o ). При отсчете каждого угла делается насечка на окружности. Для построения прямоугольника остается соединить прямыми отрезками отмеченные насечки.

Второй способ предполагает использование только циркуля и линейки. Он является несколько сложным в сравнении с предыдущим. Ниже приводится видео, где подробно объясняется каждый шаг такого построения.

Заметим, что пятиугольник легко нарисовать, если соединить концы звезды. Если нет необходимости чертить точно правильный пятиугольник, тогда можно использовать способ со звездой, нарисованной от руки.

Как только пятиугольник изображен, следует из каждой его вершины провести пять одинаковых параллельных отрезков и соединить их вершины. Получится пятиугольная призма.

Видео:Построение пятиугольника циркулемСкачать

Площадь фигуры

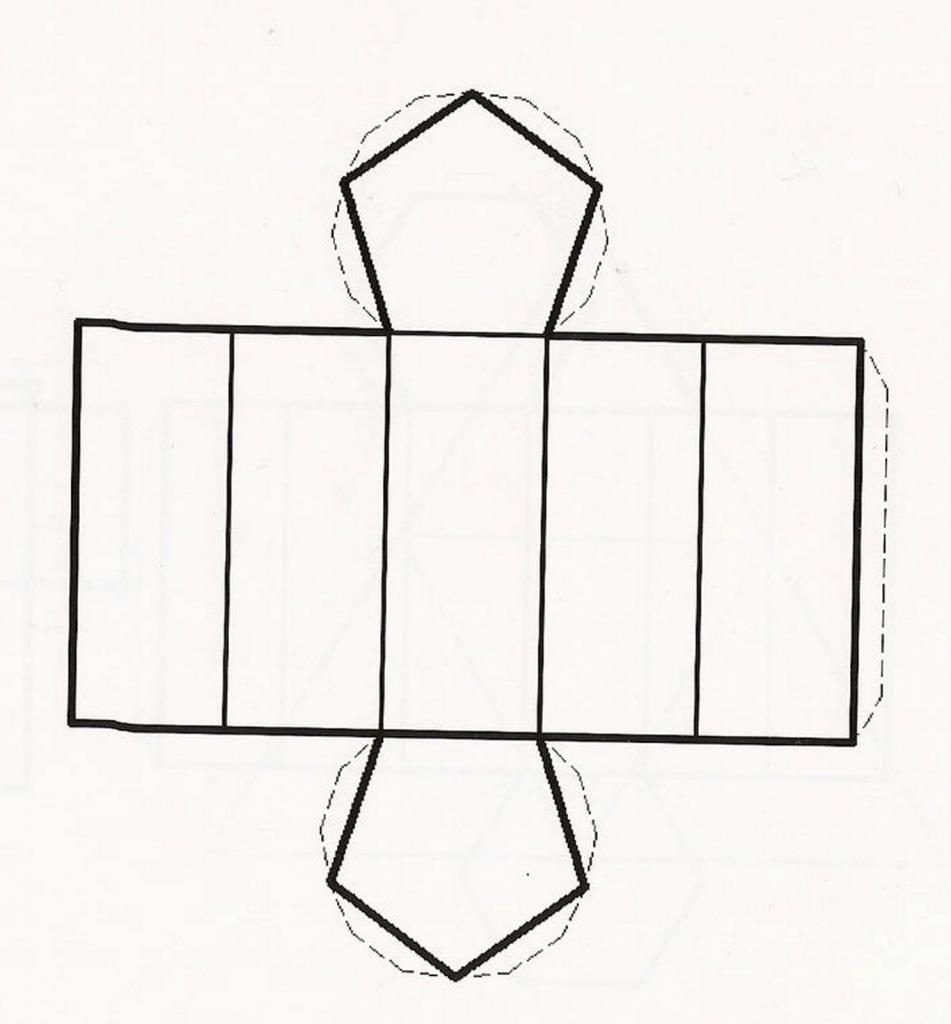
Теперь рассмотрим вопрос, как найти площадь пятиугольной призмы. На рисунке ниже приведена ее развертка. Видно, что искомая площадь образована двумя одинаковыми пятиугольниками и пятью равными друг другу прямоугольниками.

Площадь всей поверхности фигуры выразится формулой:

Здесь индексы o и p означают основание и прямоугольник соответственно. Обозначим длину стороны пятиугольника как a, а высоту фигуры как h. Тогда для прямоугольника запишем:

Чтобы вычислить площадь пятиугольника, воспользуемся универсальной формулой:

Где n — число сторон многоугольника. Подставляя n = 5, получаем:

Точность полученного равенства составляет 3 знака после запятой, что вполне достаточно для решения любых задач.

Теперь остается найти сумму полученных площадей основания и боковой поверхности. Имеем:

Следует помнить, что полученная формула справедлива только для прямоугольной призмы. В случае с косоугольной фигурой площадь ее боковой поверхности находят, исходя из знания периметра среза, который должен быть перпендикулярен всем параллелограммам.

Видео:Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

Объем фигуры

Формула расчета объема пятиугольной призмы ничем не отличается от аналогичного выражения для любой другой призмы или цилиндра. Объем фигуры равен произведению ее высоты на площадь основания:

Если рассматриваемая призма является прямоугольной, тогда высота в ней является длиной ребра, образованного прямоугольниками. Площадь правильного пятиугольника была вычислена выше с высокой точностью. Подставим это значение в формулу для объема и получим необходимое выражение для пятиугольной правильной призмы:

Таким образом, вычисление объема и площади поверхности пятиугольной правильной призмы возможно, если известна сторона основания и высота фигуры.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Правильная пятиугольная призма

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Пятиугольная призма — это многогранник, две грани которого являются равными пятиугольниками, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими пятиугольниками.

Правильная пятиугольная призма — это пятиугольная призма у которой основания правильные пятиугольники (все стороны которых равны, углы между сторонами основания составляют 108 градусов), а боковые грани прямоугольники.

Основания призмы являются равными правильными пятиугольниками.

Боковые грани призмы являются прямоугольниками.

Боковые рёбра призмы параллельны и равны.

Размеры призмы можно выразить через длину стороны a и высоту h.

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.

Формула площади поверхности пятиугольной призмы:

Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

ЗАДАНИЕ 9 «ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ»

Образец выполнения задания представлен в приложении 7.

Построить три изображения предмета по его описанию. Выполнить необходимые разрезы и сечения. Предмет изобразить с двумя отверстиями — призматическим и цилиндрическим. Работу выполнить на формате А3.

УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАНИЯ.

1. Построив три вида внешней формы предмета, рекомендуется выполнить на главном виде призматическое отверстие по форме и размерам, приведенным в таблице. Затем построить тонкими линиями проекции этого отверстия на видах сверху и сбоку. После этого построить проекции цилиндрического отверстия, начав построение с вида сверху.

2. После построения трек видов нужно выполнить разрезы. При заданных формах предмета потребуется выполнять три разреза — горизонтальный, фронтальный и профильный. Правила обозначения и изображения разрезов должны соответствовать ГОСТ 2.305-68. При симметричных изображениях следует соединить половину разреза с половиной вида. При этом на виде не показывают штриховыми линиями внутренний контур.

3. После построения изображений надо нанести размеры в соответствии с ГОСТ 2.307-68. Обратите внимание на то, что ни один из размеров не должен повториться на других изображениях.

4. Заключительный этап выполнения задания — построение сечения.