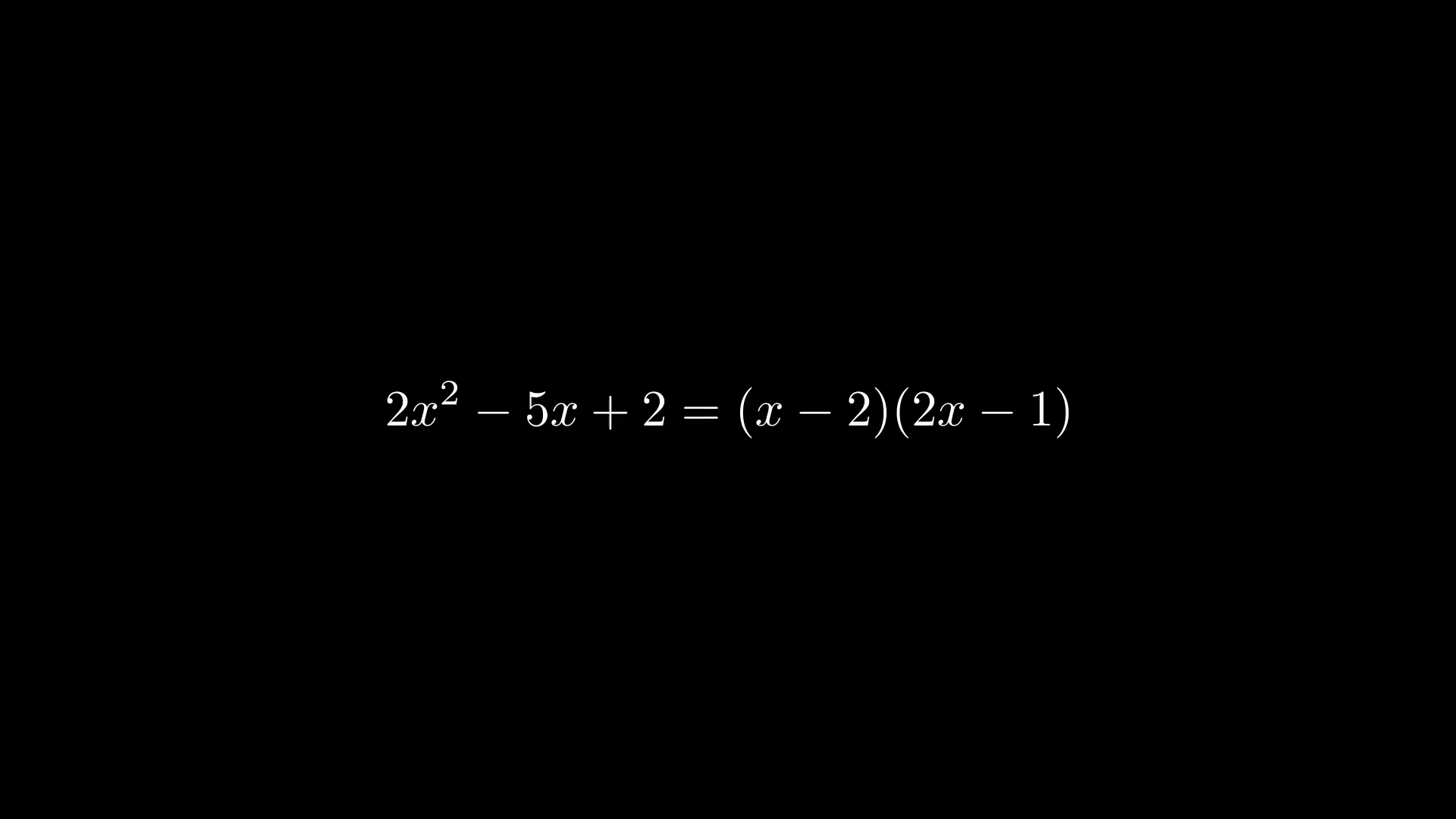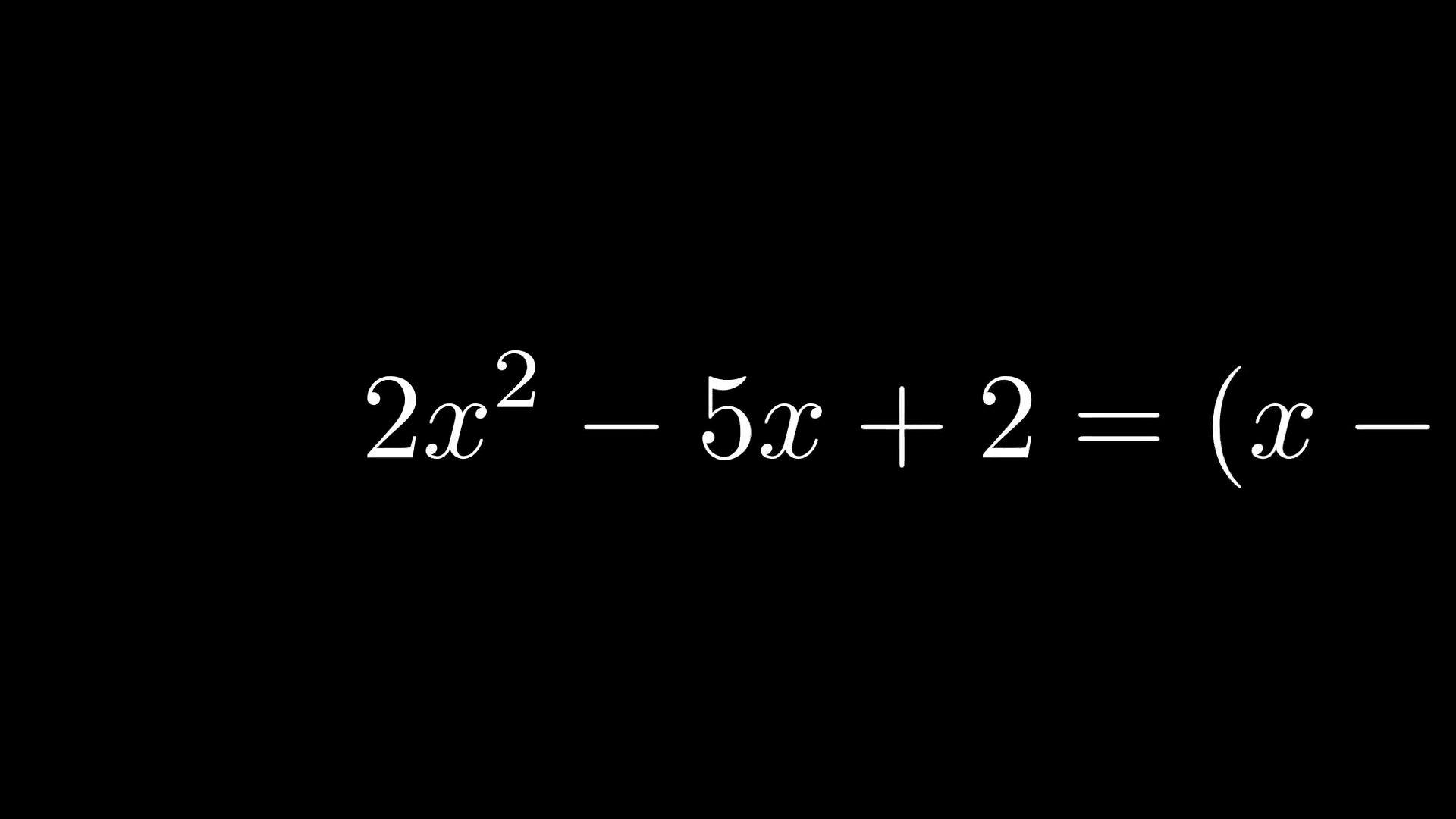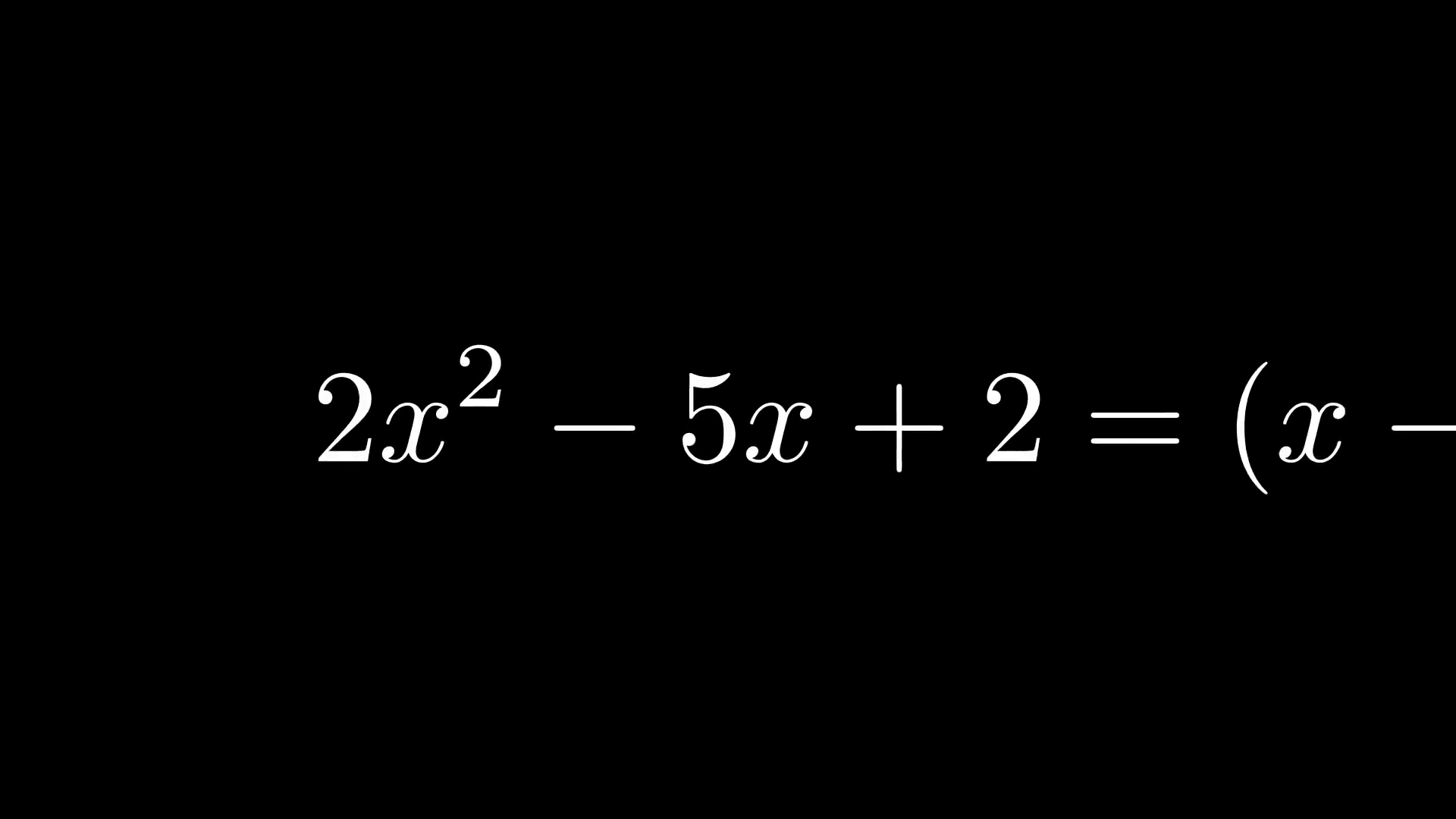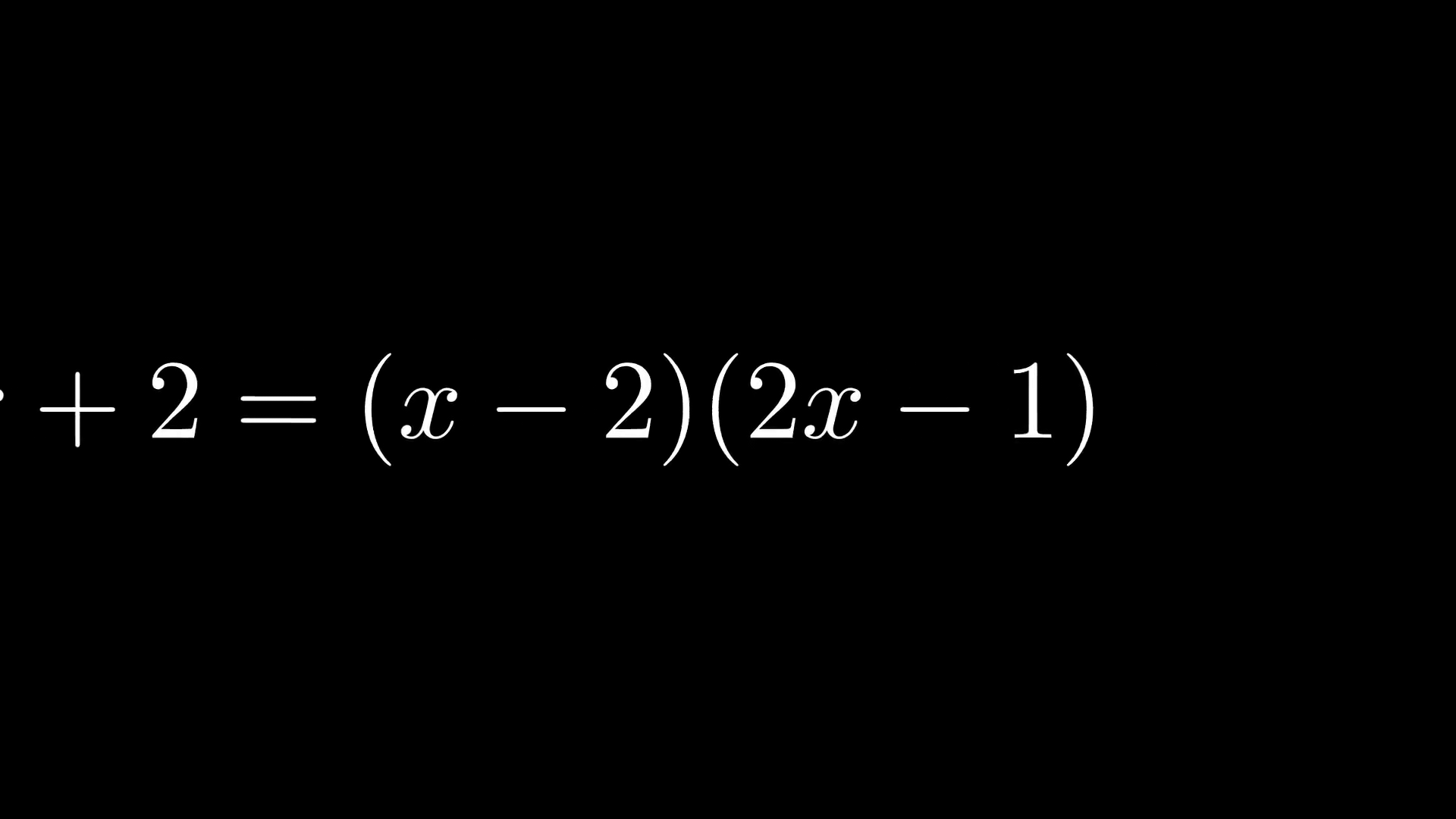Python движение по окружности

Видео:Физика - движение по окружностиСкачать

Непрерывное движение объекта в Pygame вдоль осей X, Y и по диагонали

Как показывает практика, движение — это жизнь! Поэтому сегодня мы вдохнем жизнь в сотворенный посредством Pygame объект и научим его двигаться без учета сигналов с клавиатуры! Для начала мы рассмотрим движение объекта в Pygame по прямой вдоль оси X, затем развернем объект и зададим ему движение вдоль оси Y, и в заключение — оформим диагональное перемещение объекта. Однако сначала предлагаю взглянуть на исходный код.

Исходные данные

Давайте взглянем на исходный код: у нас имеется экран csreen шириной 500px и высотой 300px, а также изображение мыши «mouse.png», расположенное на экране по заданным координатам: mouseX = 0, mouseY = 200:

При запуске кода мы увидим в левом нижнем углу экрана притаившуюся мышку с повернутой вправо мордочкой:

Что будем делать?

Необходимо научить мышку двигаться непрерывно:

• по горизонтали вдоль оси Х
• по вертикали вдоль оси Y
• по диагонали из левого нижнего угла в правый верхний угол

Общий принцип непрерывного движения в Pygame на примере движения вдоль оси X

В настоящий момент для вывода изображения мышки на экран мы используем цикл while (while True: ..) . То есть пока открыто игровое поле, мы осуществляем вывод изображения на экран в цикле по заданным координатам через каждые 30 мс (что определено строкой pygame.time.delay(30)).

В одной секунде содержится 1000 миллисекунд

Так как под движением в Pygame подразумевается перемещение объекта на заданную позицию через определенный промежуток времени, то для смещения мыши на 5px каждые 30 мс, нужно в цикле while увеличивать значение координаты X на 5px. Для этого добавим в исходный код всего 2 строчки: строку с определением переменной скорости speed, в которой будем хранить заданное смещение 5px расположим перед циклом while; а строку, задающее смещение изображение: mouseX += speed расположим в теле цикла while. В итоге получим зеленую поляну с мышкой, бегущей по горизонтальной прямой:

Код непрерывного движения объекта в Pygame по горизонтали:

Непрерывное движение объекта в Pygame вдоль оси Y

Для наглядности, сдвинем начальную позицию мышки ближе к центру, переопределив переменные стартовой позиции, как mouseX=200 и mouseY=200.

В соответствии с описанным выше принципом, зададим объекту движение по горизонтали, только изменять будем координату mouseY. В связи с тем, что точка с нулевыми координатами в Pygame располагается в верхнем левом углу поля, то при движении объекта вверх, значение координаты Y будет уменьшаться на заданное в переменной speed значение: Y -= speed. Однако, прежде чем мы добавим эту строчку в цикл while, предлагаю развернуть нашу мышку мордочкой вправо(т.е. на 90 градусов) с помощью функции pygame.transform.rotate(mouse, 90):

Код непрерывного движения объекта в Pygame по вертикали

Полученный результат:

Непрерывное движение объекта по диагонали в Pygame

При движении объекта по диагонали происходит одновременное смещение как по оси X, так и по оси Y, поэтому добавим в цикл while строки с изменением значений этих координат. Так как мы планируем движение мыши из левого нижнего угла в правый верхний угол прямоугольного экрана, то:

1. Сначала повернем мышь так, чтобы ее мордочка смотрела по направлению движения. Для этого используем функцию pygame.transform.rotate(mouse, 30).

2. Затем подкорректируем стартовую позицию объекта, чтобы повернутое изображение «выезжало» точно из левого нижнего угла: moveX=-13, moveY=218.

3. После этого, в цикле while зададим смещение по оси Х на величину speed: mouseX += speed. Кроме того, определим смещение по оси Y: так как размер игровой сцены 500×300, то при движении к правому верхнему углу поля, смещение мыши по оси Y должно быть меньше горизонтального смещения примерно в 300/500 или в 3/5 раз. Таким образом, определим смещение по Y, как: mouseY -= 3/5*speed.

Посмотрим, как будет выглядеть код после внесенных в него изменений:

Код непрерывного движения объекта в Pygame по диагонали

А теперь посмотрим на получившийся результат:

Видео:Математика это не ИсламСкачать

Вращение 2D объекта по окружности

Привет, если ты читаешь эту статью, значит ты хочешь узнать ответ на вопрос «как работает вращение объекта в 2D ?»

Ты скорее всего знаешь что во всех современных движках, таких как Unity вращение осуществляется с помощью функции, но нам интересно, как можно написать алгоритм
вращения своими руками.

Если проще то наш алгоритм работает так.

Мы представляем окружность, где:

1. Центр это точка, вокруг которой мы вращаем объект.
2. Радиус — расстояние от центра до вращаемого объекта.

Итак, начнем.

Давайте взглянем на рисунок ниже:

Дано: длинна радиуса, координаты точки вращения, угол АОВ, АВ перпендикулярен оси ОХ.
Задача: Задать вращение точки А на 360 градусов с помощью формулы.
Рассмотрим: треугольник ОАВ:
угол ОВА — прямой => треугольник ОАВ — прямоугольный треугольник;
тогда:
гипотенуза = радиусу окружности с центром в точке О
угол поворота = от 1 до 360 градусов
тогда чтобы найти катеты ОВ и АВ нужно:
АВ = радиус * cos(угла поворота),
ОВ = $inline$радиус * sin(угла поворота)$inline$
Теперь когда мы знаем размеры катетов
мы составим формулу:
для координаты по x:$inline$позиция по x = радиус * cos(угла поворота) + начальная позиция по x$inline$,
и для координаты по y: $inline$позиция по y = радиус * sin(угла поворота) + начальная позиция по y$inline$

Давайте попробуем применить формулы:

Не сложно догадаться что делает этот код, а именно вращает наш кружок по оси, но почему лишь один раз?

Давайте вспомним уроки геометрии в седьмом классе: градусная мера угла не может превышает 360 градусов.

А если попробуем обнулять угол вращения, когда тот будет больше 360 градусов, давайте посмотрим что из этого выйдет:

Этот код позволяет вращать кружок по оси бесконечно.

Однако у этой формулы есть один недостаток: можно вращать объекты только на 1 оборот. Это значит что нам нужна другая формула.

Давайте улучшим нашу формулу:

Дано:
треугольник ОАВ — прямоугольный
катет 1 = x1 — начальная координата X
катет 2 = y1 — начальная координата y

Задача:
улучшить формулу так, что-бы можно было вращать точку А на неизвестный угол.

Решение:
Из предыдущей задачи мы знаем что:
$inline$$inline$xPos = (lineLong * cos(a)) + StartPosX$inline$$inline$. => $inline$cos(a) = xPos — startPosX: (lineLong )$inline$

И теперь мы можем вывести формулу по нахождению угла a
$inline$yPos = (lineLong * sin(a)) + StartPosY$inline$ => $$display$$a = arccos((xPos — startPosX): lineLong)$$display$$.

А сейчас обновим нашу формулу и получим: $$display$$xPos = (lineLong * cos(a +b)) + startPosX$$display$$

Теперь у нас есть формула которая позволяет бесконечно вращать точку по окружности: $$display$$xPos = (lineLong * cos(a +arccos((xPos — startPosX): lineLong))) + startPosX$$display$$

Давайте напишем код, который будет вращать наш объект по нажатию на клавишу.

Примерно таком образом решается эта задача.

Надеюсь, ты смог извлечь полезную информацию из моего поста, желаю удачно применить полученные знания на практике

Видео:АЛГОРИТМ ДВИЖЕНИЯ ПО ОКРУЖНОСТИСкачать

🎞️ Как с помощью Python делать красивые математические анимации

Видео:Как начертить круг на python? #python #питон #программированиеСкачать

Leo Matyushkin

3Blue1Brown – популярный математический YouTube-канал Гранта Сандерсона. Мы и сами любим 3Blue1Brown за отличные объяснения и классные анимации. Библиотека программиста публиковала конспекты и видеоподборки по линейной алгебре, математическому анализу и наглядному введению в нейросети. Ниже представлен незначительно сокращенный перевод публикации аналитика данных Хуен Тран о создании подобных анимаций с помощью Python.

Было бы здорово знать, как создавать подобные анимации, чтобы иметь возможность объяснить идеи из научного мира своим товарищам по команде, менеджерам или подписчикам. К счастью, автор канала собрал пакет manim (сокр. mathematical animation), который позволяет создавать математические анимации и изображения с помощью Python.

Пример построения с помощью manim

Библиотека стала довольно популярной: от оригинальной версии, созданной Грантом, сообществом Manim был сделан форк. Эта версия обновляется чаще и лучше тестируется, поэтому мы будем использовать её. Версия работает для Python 3.6+ и может требовать установки дополнительных зависимостей. В остальном всё как обычно:

Видео:Разработка игры на Python | Pygame. Урок #2Скачать

Приступим к созданию анимаций

Видео:Простая анимация на питоне #программирование #pythonСкачать

Анимация растущего квадрата

Начнем с анимации квадрата, увеличивающегося в размерах из центра экрана. Код для создания анимации находится внутри метода construct в классе, наследованном от Scene .

Сохраним скрипт под именем start.py и запустим в терминале команду, чтобы сгенерировать видео:

В результате скрипт создаст и сохранит видео под названием PointMovingOnShapes.mp4 . Запустив его, мы увидим что-то вроде того, что показано ниже.

Результат анимации движения квадрата

В команде для терминала использовались следующие опции:

• -p : воспроизвести видео после того, как оно сгенерировано.
• -ql : сохранить видео в низком качестве (меньший размер файла). Для генерации в высоком качестве используем -qh .

Чтобы вместо видео сгенерировать гифку, добавляем -i , например:

Видео:Как Работать с Физикой на Python. Доска Гальтона [ Pygame + Pymunk ]Скачать

Превращаем квадрат в окружность

Создание квадрата не так уж интересно. Превратим его в окружность.

Трансформация фигуры

Полный список фигур доступен в документации.

Видео:Графика в Python. Анимация. Передвижение объектов.Скачать

Настраиваем фон

Если нужно, чтобы фон имел другой цвет, задаем config.background_color .

Изменяем фон с черного на серый

Другие возможности кастомизации описаны здесь.

Видео:Uniform Circular Motion | Python #shortsСкачать

Делаем динамическую рамку для частей уравнения

Можно показать, как пошагово решить уравнение:

Пошаговое решение

Видео:Функции trunc, floor, ceil. Округление вверх и вниз в pythonСкачать

Перемещаем и масштабируем формулы

Можно настроить положение «камеры» и область увеличения с помощью наследования класса от MovingCameraScene .

Видео:#5. Математические функции и работа с модулем math | Python для начинающихСкачать

Рисуем графики

Библиотеку manim можно также использовать для создания аннотированных графиков.

Если нужно получить изображение последнего кадра сцены, добавляем к команде -s :

Можно сделать изображение более динамичным, если анимировать процесс настройки осей, установив animate = True .

Анимация осей статичного графика

Видео:Сделал игру, на python в консолиСкачать

Совместное перемещение объектов

Чтобы группировать различные объекты и перемещать их вместе, используем VGroup .

Движение двух групп объектов

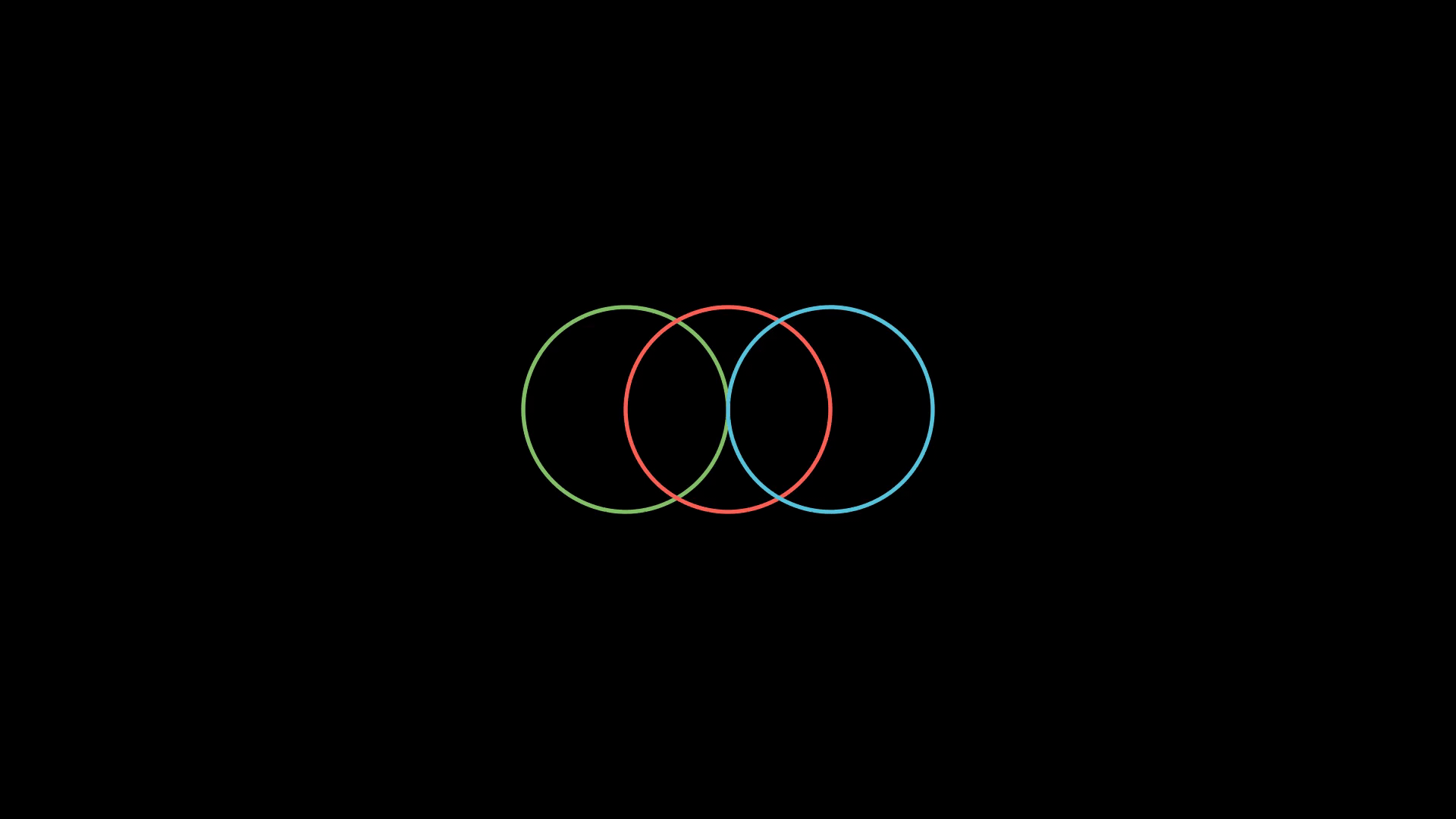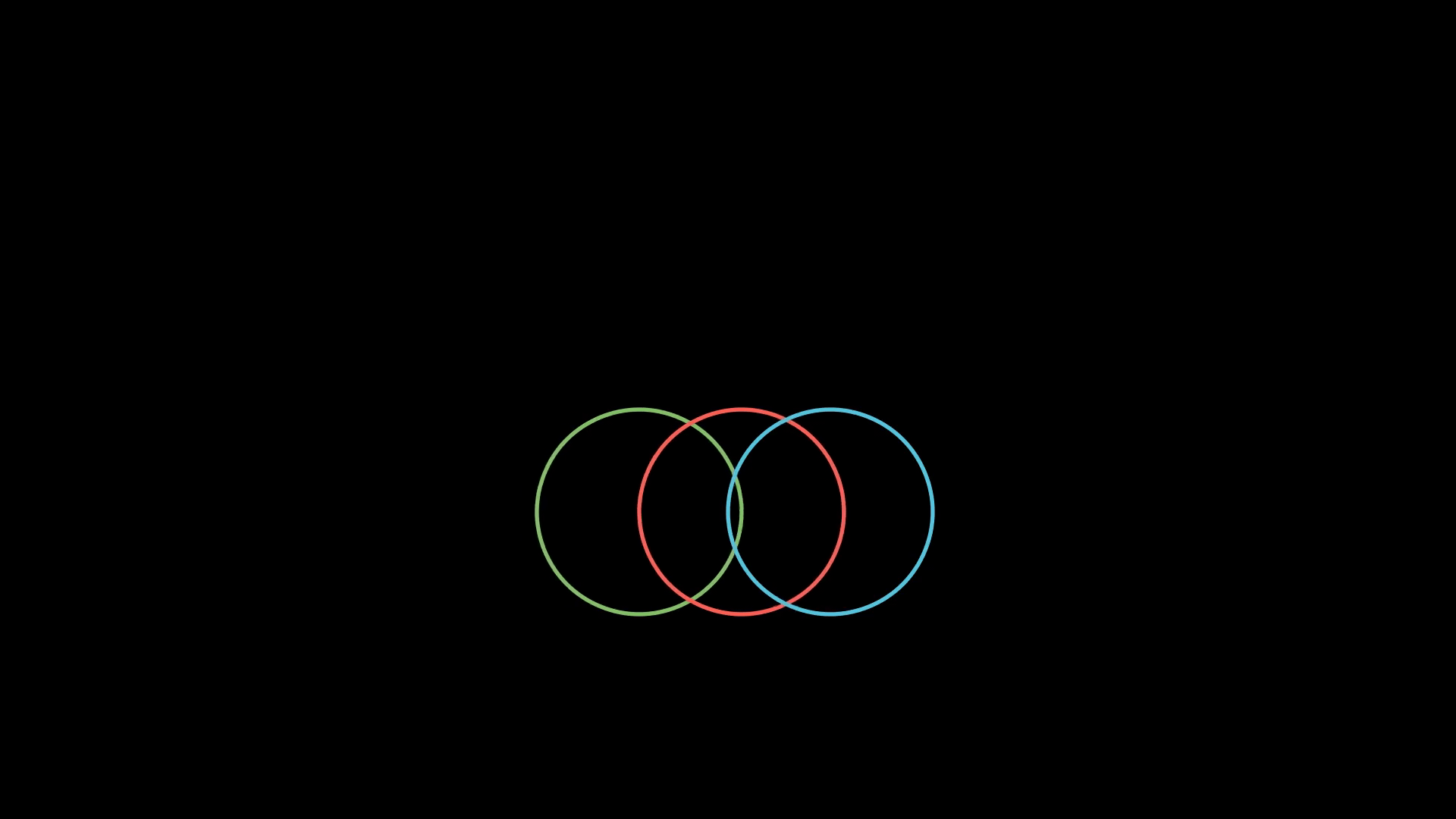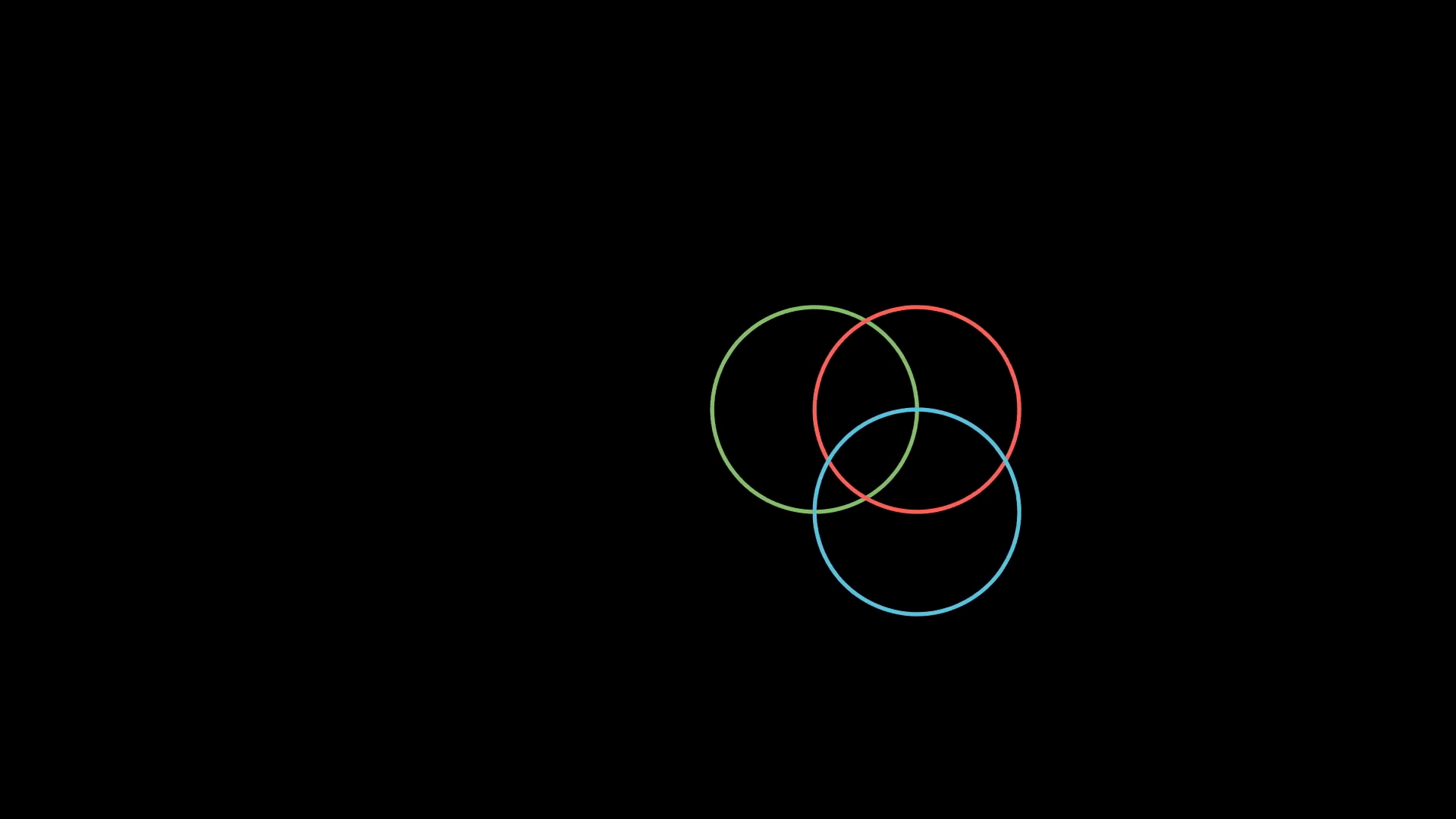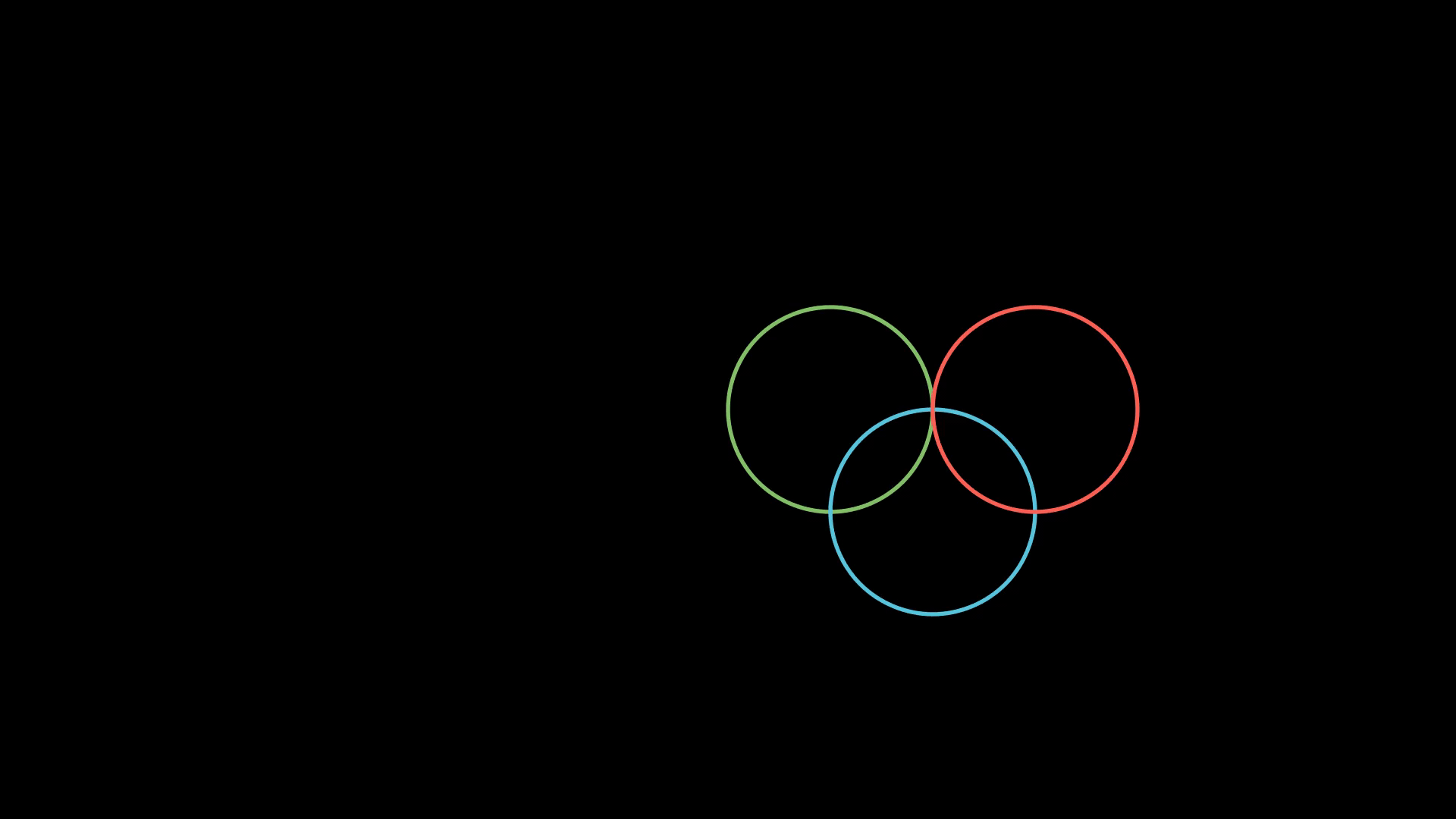
Видео:Игра на питоне 🎮 #python #программирование #разработкаСкачать

Трассировка движения фигуры

Для создания следа движущегося объекта, применяем TracedPath :

Трассировка движения фигуры

Видео:#PYTHON# ДВИЖЕНИЕ КУБИКА НА PYGAMEСкачать

Заключение

В этом небольшом туториале мы рассмотрели несколько способов, как можно анимировать математические абстракции с помощью библиотеки manim . Из приведенных примеров вы могли заметить, что manim предоставляет три вида объектов:

• Mobjects: объекты, которые могут быть показаны на экране: Circle , Square , Matrix , Angle и т. д.
• Scenes: сцены для построения анимации: Scene , MovingCameraScene и др.
• Animations: анимационные эффекты, применяемые к Mobjects – такие, как Write , Create , GrowFromCenter , Transform .

Лучший способ научиться работать с такими объектами – делать собственные анимации. Другие примеры использования можно подсмотреть в руководстве по manim.

Скрипты из этой статьи также доступны в GitHub-репозитории.

На Python создают прикладные приложения, пишут тесты и бэкенд веб-приложений, автоматизируют задачи в системном администрировании, его используют в нейронных сетях и анализе больших данных. Язык можно изучить самостоятельно, но на это придется потратить немало времени. Если вы хотите быстро понять основы программирования на Python, обратите внимание на онлайн-курс «Библиотеки программиста». За 30 уроков (15 теоретических и 15 практических занятий) под руководством практикующих экспертов вы не только изучите основы синтаксиса, но и освоите две интегрированные среды разработки (PyCharm и Jupyter Notebook), работу со словарями, парсинг веб-страниц, создание ботов для Telegram и Instagram, тестирование кода и даже анализ данных. Чтобы процесс обучения стал более интересным и комфортным, студенты получат от нас обратную связь. Кураторы и преподаватели курса ответят на все вопросы по теме лекций и практических занятий.

🎥 Видео

[Python] Введение в распознавание контуров через OpenCVСкачать

Игра для изучения Python с нуля, для начинающих программистов #shorts #программирование #pythonСкачать

5 Processing движение по окружностиСкачать

Модули и классы в языке Python. Окружности и дуги.Скачать