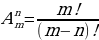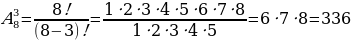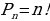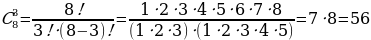Видео:Математика без Ху!ни. Теория вероятностей, комбинаторная вероятность.Скачать
«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
Перестановки. Формула для числа перестановок
Пусть множество Х состоит из n элементов.
Определение. Размещение без повторений из n элементов множества X по n называется перестановкой из n элементов.
Заметим, что в любую перестановку входят все элементы множества Х , причём ровно по одному разу. То есть перестановки одна от другой отличаются только порядком следования элементов и могут получиться одна из другой перестановкой элементов (отсюда и название).
Число всех перестановок из n элементов обозначается символом 
.
Так как перестановки – это частный случай размещений без повторений при 
, то формулу для нахождения числа получим из формулы (2), подставляя в неё :
(3)
Пример. Сколькими способами можно разместить на полке 5 книг?
Решение. Способов размещения книг на полке существует столько, сколько существует различных перестановок из пяти элементов: 
способов.
Замечание. Формулы (1)-(3) запоминать не обязательно: задачи на их применение всегда можно решить с помощью правила произведения. Если у учащихся существуют проблемы с составлением комбинаторных моделей задач, то лучше сделать более узким множество используемых формул и правил (чтобы было меньше возможности ошибиться). Правда, задачи, в которых используются перестановки и формула (3), обычно решаются без особых проблем.
1. Ф. Сколькими способами могут встать в очередь в билетную кассу: 1) 3 человека; 2) 5 человек?
Различные варианты расположения п человек в очереди отличаются один от другого только порядком расположения людей, т. е. являются различными перестановками из п элементов.
Три человека могут встать в очередь Р3 = 3! = 6 различными способами.
Ответ: 1) 6 способов; 2) 120 способов.
2. Т. Сколькими способами 4 человека могут разместиться на четырехместной скамейке?
Количество человек равно количеству мест на скамейке, поэтому количество способов размещения равно числу перестановок из 4 элементов: Р4 = 4! = 24.
Можно рассуждать по правилу произведения: для первого человека можно выбрать любое из 4 мест, для второго — любое из 3 оставшихся, для третьего — любое из 2 оставшихся, последний займет 1 оставшееся место; всего есть 
= 24 разных способов Размещения 4 человек на четырехместной скамейке.
Ответ: 24 способами.
3. М. У Вовы на обед — первое, второе, третье блюда и пирожное. Он обязательно начнет с пирожного, а все остальное съест в произвольном порядке. Найдите число возможных вариантов обеда.
М- задачи из уч. пособия А.Г.Мордковича
Т- под ред. С.А.Теляковского
После пирожного Вова может выбрать любое из трех блюд, затем — из двух, и закончить оставшимся. Общее число возможных вариантов обеда: 
=6.
4. Ф. Сколько различных правильных (с точки зрения русского языка) фраз можно составить, изменяя порядок слов в предложении: 1) «Я пошел гулять»; 2) «Во дворе гуляет кошка»?
Во втором предложении предлог «во» должен всегда стоять перед существительным «дворе», к которому он относится. Поэтому, считая пару «во дворе» за одно слово, можно найти количество различных перестановок трех условных слов: Р3 = 3! = 6. Таким образом, и в этом случае можно составить 6 правильных предложений.
5. Сколькими способами можно с помощью букв К, L, М, Н обозначить вершины четырехугольника?
Будем считать, что вершины четырехугольника пронумерованы, за каждой закреплен постоянный номер. Тогда задача сводится к подсчету числа разных способов расположения 4 букв на 4 местах (вершинах), т. е. к подсчету числа различных перестановок: Р4 = 4! =24 способа.
Ответ: 24 способа.
6. Ф. Четыре друга купили билеты в кино: на 1-е и 2-е места в первом ряду и на 1-е и 2-е места во втором ряду. Сколькими способами друзья могут занять эти 4 места в кинотеатре?
Четыре друга могут занять 4 разных места Р4 = 4! = 24 различными способами.
Ответ: 24 способа.
7. Т. Курьер должен разнести пакеты в 7 различных учреждений. Сколько маршрутов может он выбрать?
Под маршрутом следует понимать порядок посещения курьером учреждений. Пронумеруем учреждения номерами от 1 до 7, тогда маршрут будет представляться последовательностью из 7 Цифр, порядок которых может меняться. Количество маршрутов равно числу перестановок из 7 элементов: Р7= 7! = 5 040.
Ответ: 5 040 маршрутов.
8. Т. Сколько существует выражений, тождественно равных произведению abcde, которые получаются из него перестановкой множителей?
Дано произведение пяти различных сомножителей abcde, порядок которых может меняться (при перестановке множителей произведение не меняется).
Всего существует Р5 = 5! = 120 различных способов расположения пяти множителей; один из них (abcde) считаем исходным, остальные 119 выражений тождественно равны данному.
Ответ: 119 выражений.
9. Т. Ольга помнит, что телефон подруги оканчивается цифрами 5, 7, 8, но забыла, в каком порядке эти цифры следуют. Укажите наибольшее число вариантов, которые ей придется перебрать, чтобы дозвониться подруге.
Три последних цифры телефонного номера могут быть расположены в одном из Р3 =3! =6 возможных порядков, из которых только один верный. Ольга может сразу набрать верный вариант, может набрать его третьим, и т. д. Наибольшее число вариантов ей придется набрать, если правильный вариант окажется последним, т. е. шестым.
Ответ: 6 вариантов.
10. Т. Сколько шестизначных чисел (без повторения цифр) можно составить из цифр: а) 1,2, 5, 6, 7, 8; б) 0, 2, 5, 6, 7, 8? Решение.
а) Дано 6 цифр: 1, 2, 5, 6, 7, 8, из них можно составлять разные шестизначные числа, только переставляя эти цифры местами. Количество различных шестизначных чисел при этом равно Р6 = 6! = 720.
б) Дано 6 цифр: 0, 2, 5, 6, 7, 8, из них нужно составлять различные шестизначные числа. Отличие от предыдущей задачи состоит в том, что ноль не может стоять на первом месте.
Можно напрямую применить правило произведения: на первое место можно выбрать любую из 5 цифр (кроме нуля); на второе место — любую из 5 оставшихся цифр (4 «ненулевые» и теперь считаем ноль); на третье место — любую из 4 оставшихся после первых двух выборов цифр, и т. д. Общее количество вариантов равно: 
= 600.
Можно применить метод исключения лишних вариантов. 6 цифр можно переставить Р6 = 6! = 720 различными способами. Среди этих способов будут такие, в которых на первом месте стоит ноль, что недопустимо. Подсчитаем количество этих недопустимых вариантов. Если на первом месте стоит ноль (он фиксирован), то на последующих пяти местах могут стоять в произвольном порядке «ненулевые» цифры 2, 5, 6, 7, 8. Количество различных способов, которыми можно разместить 5 цифр на 5 местах, равно Р5 = 5! = 120, т. е. количество перестановок чисел, начинающихся с нуля, равно 120. Искомое количество различных шестизначных чисел в этом случае равно: Р6 — Р5 = 720 — 120 = 600.
Ответ: а) 720; б) 600 чисел.
11. Т. Сколько среди четырехзначных чисел (без повторения цифр), составленных из цифр 3, 5, 7, 9, таких, которые: а) начинаются с цифры 3;
а) Из цифр 3, 5, 7, 9 составляем четырехзначные числа, начинающиеся с цифры 3.
Фиксируем цифру 3 на первом месте; тогда на трех оставшихся местах в произвольном порядке могут располагаться цифры 5, 7 9 Общее количество вариантов их расположения равно Р 3 = 3!=6. Столько и будет разных четырехзначных чисел, составленных из данных цифр и начинающихся с цифры 3.
б) Заметим, что сумма данных цифр 3 + 5 + 7 + 9 = 24 делится на 3, следовательно, любое четырехзначное число, составленное из этих цифр, делится на 3. Для того, чтобы некоторые из этих чисел делились на 15, необходимо, чтобы они заканчивались цифрой 5.
Фиксируем цифру 5 на последнем месте; остальные 3 цифры можно разместить на трех местах перед 5 Рз = 3! = 6 различными способами. Столько и будет разных четырехзначных чисел, составленных из данных цифр, которые делятся на 15.
Ответ: а) 6 чисел; б) 6 чисел.
12. Т. Найдите сумму цифр всех четырехзначных чисел, которые можно составить из цифр 1, 3, 5, 7 (без их повторения).
Каждое четырехзначное число, составленное из цифр 1, 3, 5, 7 (без повторения), имеет сумму цифр, равную 1+3 + 5 + 7=16.
Из этих цифр можно составить Р4 = 4! = 24 различных числа, отличающихся только порядком цифр. Сумма цифр всех этих чисел будет равна
16 
= 384.
13. Т. Семь мальчиков, в число которых входят Олег и Игорь, становятся в ряд. Найдите число возможных комбинаций, если:
а) Олег должен находиться в конце ряда;
б) Олег должен находиться в начале ряда, а Игорь — в конце ряда;
в) Олег и Игорь должны стоять рядом.
Решение.
а) Всего 7 мальчиков на 7 местах, но один элемент фиксирован, не переставляется (Олег находится в конце ряда). Число возможных комбинаций при этом равно числу перестановок 6 мальчиков, стоящих перед Олегом: Р6=6!=720.
пару как единый элемент, переставляемый с другими пятью элементами. Число возможных комбинаций тогда будет Р6 = 6! = 720.
Пусть теперь Олег и Игорь стоят рядом в порядке ИО. Тогда получим еще Р6 = 6! = 720 других комбинаций.
Общее число комбинаций, в которых Олег и Игорь стоят рядом (в любом порядке) равно 720 + 720 = 1 440.
Ответ: а) 720; б) 120; в) 1 440 комбинаций.
14. М. Одиннадцать футболистов строятся перед началом матча. Первым становится капитан, вторым — вратарь, а остальные — случайным образом. Сколько существует способов построения?
После капитана и вратаря третий игрок может выбрать любое из 9 оставшихся мест, следующий — из 8, и т. д. Общее число способов построения по правилу произведения равно:
1 
=362 880, или 
Р 9 = 9! = 362 880.
15. М. Сколькими способами можно обозначить вершины куба буквами А, В, С, D, E, F, G, K?
Для первой вершины можно выбрать любую из 8 букв, для второй — любую из 7 оставшихся, и т. д. Общее число способов по правилу произведения равно 
=40 320, или Р8 = 8!
16. Т. В расписании на понедельник шесть уроков: алгебра, геометрия, биология, история, физкультура, химия. Сколькими способами можно составить расписание уроков на этот день так, чтобы два урока математики стояли рядом?
Всего 6 уроков, из них два урока математики должны стоять рядом.
«Склеиваем» два элемента (алгебра и геометрия) сначала в порядке АГ, затем в порядке ГА. При каждом варианте «склеивания» получаем Р5 = 5! = 120 вариантов расписания. Общее число способов составить расписание равно120 (AГ) +120 (ГА) = 240.
Ответ: 240 способов.
17. Т. Сколько существует перестановок букв слова «конус», в которых буквы К, О, Н стоят рядом?
Дано 5 букв, из которых три буквы должны стоять рядом. Три буквы К, О, Н могут стоять рядом одним из Р3 = 3! = 6 способов. Для каждого способа «склеивания» букв К, О, Н получаем Р3 = 3! = 6 способов перестановки букв, «склейка», У, С. Общее число различных перестановок букв слова «конус», в которых буквы К, О, Н стоят рядом, равно 6 • 6 = 36 перестановок- анаграмм.
Ответ: 36 анаграмм.
18. Т. Сколькими способами 5 мальчиков и 5 девочек могут занять в театре в одном ряду места с 1 по 10? Сколькими способами они могут это сделать, если мальчики будут сидеть на нечетных местах, а девочки — на четных?
Каждый вариант расположения мальчиков может сочетаться с каждым из вариантов расположения девочек, поэтому по правилу произведения общее число способов рассадить детей в этом случае равно 120 
20= 14400.
Ответ: 3 628 800 способов; 14 400 способов.
19. Т. Пять мальчиков и четыре девочки хотят сесть на девятиместную скамейку так, чтобы каждая девочка сидела между двумя мальчиками. Сколькими способами они могут это сделать?
По условию задачи мальчики и девочки должны чередоваться, т. е. девочки могут сидеть только на четных местах, а мальчики -только на нечетных. Поэтому меняться местами девочки могут только с девочками, а мальчики — только с мальчиками. Четырех девочек можно рассадить на четырех четных местах Р4 = 4! = 24 способами, а пятерых мальчиков на пяти нечетных местах Р5 = 5! = 120 способами.
Каждый способ размещения девочек может сочетаться с каждым способом размещения мальчиков, поэтому по правилу произведения общее число способов равно: Р4 
20 = 2 880 способов.
Ответ: 2 880 способов.
20. Ф. Разложить на простые множители числа 30 и 210. Сколькими способами можно записать в виде произведения продых множителей число: 1) 30; 2) 210?
Разложим данные числа на простые множители:
30 = 2 
; 210 = 2 
.
Число 30 можно записать в виде произведения простых множителей
Р 3 = 3! = 6 разными способами (переставляя множители).
Число 210 можно записать в виде произведения простых
множителей Р 4 = 4! = 24 разными способами.
Ответ: 1) 6 способов; 2) 24 способа.
21. Ф. Сколько различных четных четырехзначных чисел с неповторяющимися цифрами можно записать, используя цифры 1, 2, 3, 5?
Чтобы число было четным, оно должно заканчиваться четной цифрой, т. е. 2. Зафиксируем двойку на последнем месте, остальные три цифры должны стоять перед ней в произвольном порядке. Количество различных перестановок из 3 цифр равно P3 = 3! = 6; следовательно, различных четных четырехзначных чисел будет также 6 (к каждой перестановке из трех цифр добавляется цифра 2).
22. Ф. Сколько различных нечетных пятизначных чисел, в которых нет одинаковых цифр, можно записать с помощью Цифр 1,2, 4, 6, 8?
Чтобы составленное число было нечетным, необходимо, чтобы оно оканчивалось нечетной цифрой, т. е. единицей. Остальные 4 Цифры можно переставлять местами, располагая каждую перестановку перед единицей.
Общее число нечетных пятизначных чисел равно числу перестановок: Р4 = 4! =24.
23. Ф. Сколько различных шестизначных чисел с неповторяющимися цифрами можно записать с помощью цифр 1; 2 3, 4, 5, 6, если: 1) число должно начинаться с 56; 2) цифры 5 и 6 в числе должны стоять рядом?
Две цифры 5 и 6 фиксируем в начале числа и дописываем к ним различные перестановки из 4 оставшихся цифр; количество различных шестизначных чисел равно: Р4 = 4! = 24.
Условно будем считать пару 56 одной цифрой и переставлять ее с четырьмя остальными цифрами; получим Р5 = 5! = 120 различных чисел из 5 цифр, среди которых одна условная, двойная.
Если считать условной цифрой пару 65, то получим еще Р5 = 5! = = 120 различных чисел.
Общее количество различных шестизначных чисел, в которых цифры 5 и 6 стоят рядом (в любом порядке), равно 120 + 120 = 240 чисел. (Варианты 56 и 65 несовместны, не могут реализоваться одновременно; применяем комбинаторное правило суммы.)
Ответ: 1) 24 числа; 2) 240 чисел.
24. Ф. Сколько различных четных четырехзначных чисел, в записи которых нет одинаковых цифр, можно составить из цифр 1,2,3,4?
Четное число должно оканчиваться четной цифрой. Фиксируем на последнем месте цифру 2, тогда 3 предшествующие цифры можно переставить Р3 = 3! = 6 различными способами; получим 6 чисел с двойкой на конце. Фиксируем на последнем месте цифру 4, получим Р3 = 3! = 6 различных перестановок трех предшествующих цифр и 6 чисел, оканчивающихся цифрой 4.
Общее количество четных четырехзначных чисел будет 6 + 6 = 12 различных чисел.
Замечание. Общее количество вариантов мы находим, пользуясь комбинаторным правилом суммы (6 вариантов чисел, оканчивающихся двойкой, 6 вариантов чисел, оканчивающихся четверкой; способы построения чисел с двойкой и с четверкой на конце являются взаимоисключающими, несовместными, поэтому общее количество вариантов равно сумме числа вариантов с двойкой на конце и числа вариантов с 4 на конце). Запись 6 + 6 = 12 лучше отражает основания наших действий, чем запись Р 
.
25. Ф. Сколькими способами можно записать в виде произведения простых множителей число 1) 12; 2) 24; 3) 120?
Особенностью этой задачи является то, что в разложении каждого из данных чисел есть одинаковые, повторяющиеся множители. При образовании различных перестановок из множителей мы не получим новую перестановку, если поменяем местами какие-нибудь два одинаковых множителя.
1) Число 12 разлагается на три простых множителя, два из которых одинаковы: 12 = 
.
Если бы все множители были различны, то их можно было бы переставить в произведении Р3 = 3! = 6 различными способами. Чтобы перечислить эти способы, условно «различим» две двойки, подчеркнем одну из них: 12 = 2 
.
Тогда возможны следующие 6 вариантов разложения на жители: 
Но на самом деле подчеркивание цифр не имеет в математике никакого значения, поэтому полученные 6 перестановок в обычной записи имеют вид:
т. е. фактически мы получили не 6, а 3 различные перестановки Количество перестановок уменьшилось в два раза за счет того, что мы не должны учитывать перестановки двух двоек между собой.
Обозначим Р х искомое число перестановок из трех элементов среди которых два одинаковых; тогда полученный нами результат можно записать так: Рз = Р х 
Но 2 — это количество разных перестановок из двух элементов, т. е. 2 = 
= 2! = Р 2 , поэтому Р3, = Р х 
Р 2 , отсюда Р х = 
. (это формула для числа перестановок с повторениями).
Можно рассуждать иначе, основываясь только на комбинаторном правиле произведения.
Чтобы составить произведение из трех множителей, сначала выберем место для множителя 3; это можно сделать одним из трех способов. После этого оба оставшихся места заполняем двойками; это можно сделать 1 способом. По правилу произведения общее число способов равно: 3-1 =3.
2)Число 24 разлагается на четыре простых множителя, из которых три — одинаковые: 24= 
Отсюда 
Чтобы составить произведение из четырех множителей, сначала выберем место для множителя 3; это можно сделать одним из четырех способов. После этого все три оставшихся места заполним двойками; это можно сделать 1 способом (двойки неразличимы между собой, поэтому просто пишем на каждое свободное место по двойке). По правилу произведения получим 4 1=4 различных записи произведения.
3) Число 120 разлагается на 5 простых множителей (2,2,2,3,5), из которых три- одинаковые. В этом случае 
, Р х =20.
Второй способ. Составляя произведение из пяти множителей, сначала выберем место для пятерки (5 способов), затем для тройки (4 способа), а оставшиеся 3 места заполним двойками (1 способ); по правилу произведения 5 • 4 • 1 = 20.
Ответ: 1) 3; 2) 4; 3) 20.
26. Ф. Сколькими способами можно закрасить 6 клеток таким образом, чтобы 3 клетки были красными, а 3 оставшиеся были закрашены (каждая своим цветом) белым, черным или зеленым?
Перестановки из 6 элементов, среди которых три — одинаковые:
Иначе: для закраски белым цветом можно выбрать одну из 6 клеток, черным — из 5, зеленым — из 4; три оставшиеся клетки закрашиваем красным цветом. Общее число способов: 6 • 5 • 4 • 1 = 120.
Ответ: 120 способов.
27.Т. Пешеход должен пройти один квартал на север и три квартала на запад. Выпишите все возможные маршруты пешехода.
Будем обозначать каждый маршрут последовательностью из 4 букв: трех букв з и одной с. Каждая буква показывает, в каком направлении пешеход проходит очередной квартал. Выбрать маршрут — это значит выбрать для буквы с одно место из четырех возможных. Поэтому возможны следующие маршруты:
Количество различных маршрутов равно Р4 = 
Иначе: выбираем одно место из 4 для буквы с; количество вариантов равно 
= 4.
Ответ: 4 маршрута.
28. М. а) На дверях четырех одинаковых кабинетов надо повесить таблички с фамилиями четырех заместителей директора. Сколькими способами это можно сделать?
б) В 9 «А» классе в среду 5 уроков: алгебра, геометрия, физкультура, русский язык, английский язык. Сколько можно составить вариантов расписания на этот день?
в) Сколькими способами четыре вора могут разбежаться по одному на все четыре стороны?
г) Адъютант должен развезти пять копий приказа генерала пяти полкам. Сколькими способами он может выбрать маршрут доставки копий приказа?
а) Для первой таблички можно выбрать любой из 4 кабинетов,
Для второй — любой из трех оставшихся, для третьей — любой из двух оставшихся, для четвертой — один оставшийся; по правилу
произведения общее число способов равно: 4 • 3 • 2 • 1 = 24, или Р4 = 4! = 24.
б) На первый урок ставим любой из пяти предметов, на второй — из четырех, и т. д. Общее число вариантов расписания по правилу произведения равно: 
= 120, или Р5 = 5! = 120.
в) Обозначим 4 стороны как С, Ю, В, 3. Первый вор выбирает любую из четырех сторон, второй — из трех, третий — из двух, общее число способов равно: 
= 24, или Р4 = 4! = 24.
г) Под маршрутом будем понимать последовательность, посещения полков. Первым можно
посетить любой из 5 полков, после этого — любой из 4 оставшихся, и т. д. Общее число возможных маршрутов равно: = 120, или Р5 = 5! = 120.
Видео:9 класс, 26 урок, Комбинаторные задачиСкачать
Сколькими способами можно с помощью букв к а в с обозначить вершины четырехугольника решение
Ответ: 24 способа
Объяснение:
Будем считать, что вершины четырехугольника пронумерованы, за каждой закреплен постоянный номер. Тогда задача сводится к подсчету числа разных способов расположения 4 букв на 4 местах (вершинах).
Для решения данной задачи воспользуемся формулой из комбинаторики, которая определяет число перестановок.
Из формулы следует, что количество способов, которыми можно расположить 4 буквы на 4 вершинах:
Число способов, которыми 4 буквы можно разместить на 4 вершинах равно 24.
*4! — факториал 4. Факториалом числа 4 называют произведение всех натуральных чисел, меньше или равных 4.
Видео:Комбинаторика: перестановка, размещение и сочетание | Математика | TutorOnlineСкачать
Основные понятия комбинаторики
Опорный конспект и задания для самостоятельного изучения темы «Основные понятия комбинаторики»
Просмотр содержимого документа
«Основные понятия комбинаторики»
Основные понятия комбинаторики.
Факториал числа – это произведение натуральных чисел от 1 до самого числа (включая данное число). Обозначается факториал восклицательным знаком n!
Пример. Вычислить факториалы следующих чисел: 3! 5!
3! = 1·2·3 = 6 5! = 1·2·3·4·5 = 120
Комбинаторикой называют область математики, которая изучает вопросы о числе различных комбинаций (удовлетворяющих тем или иным условиям), которые можно составить из данных элементов.
(Комбинаторика – раздел математики, в котором исследуются и решаются задачи выбора элементов из исходного множества и расположения их в некоторой комбинации, составляемой по заданным правилам.)
Группы, составленные из каких-либо элементов, называются соединениями.
Различают три вида соединений: размещения, перестановки и сочетания.
Задачи, в которых производится подсчет возможных различных соединений, составленных из конечного числа элементов по некоторому правилу, называются комбинаторными, а раздел математики, занимающийся их решением, — комбинаторикой. Рассмотрим три основных вида соединений и формулы вычисления их количества. Для этого сначала рассмотрим 2 задачи, которые помогут нам сосредоточиться на сути новых понятий.
Определение. Размещениями из m элементов по n элементов
( n ≤ m ) называются такие соединения, каждое из которых содержит n элементов, взятых из m данных разных элементов, и которые отличаются одно от другого либо самими элементами, либо порядком их расположения
Число размещений из m элементов по n обозначают 
(от французского «arrangement» — «размещение») и вычисляют по формуле: 
Пример 1. 
Пример 2. 
Определение. Перестановкой из n элементов называют размещение из n элементов по n.
Число перестановок из n элементов обозначается 
и вычисляется по формуле: 
Сочетаниями из m элементов по n элементов ( n ≤ m ) называются такие соединения, каждое из которых содержит n элементов, взятых из m данных элементов, и которые отличаются друг от друга по крайней мере одним элементом.
Число сочетаний из n элементов по m обозначают 
(от французского «combination» — «сочетание») и вычисляют по формуле: 
Пример 3. 
Пример 4. 
При решении комбинаторных задач важно научиться различать виды соединений.
Пример: Сколькими способами можно с помощью букв A, B, C, D обозначить вершины четырехугольника?
Меняется только порядок расположения выбранных элементов
Пример: У лесника три собаки: Астра, Вега и Граф. На охоту лесник решил пойти с двумя собаками. Перечислите все варианты выбора лесником пары собак.
Меняется только состав входящих в комбинацию элементов, порядок их расположения не важен
Пример: Сколькими способами могут быть распределены I, II и III премии между 15-ю участниками конкурса?
Меняется состав входящих в комбинацию элементов и важен порядок их расположения
Задание: выполнить вычисления ниже таблицы, а в таблицу записать только ответы (без заданий)
🔥 Видео
Комбинаторика. Основные формулы (перестановки, сочетания, размещения) и примеры решения задач.Скачать
КОМБИНАТОРИКА для ЧАЙНИКОВ | ОЛИМПИАДНАЯ МАТЕМАТИКАСкачать
РазмещенияСкачать
Комбинаторика с повторениямиСкачать
Теория вероятностей | Математика TutorOnlineСкачать
Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать
Профильный ЕГЭ 2023 математика. Задача 17. Параметр. Графический методСкачать
Edu: Сколькими способами можно доказать теорему Пифагора?Скачать
Комбинаторика. Как решать задачи? | Дискретная математика | УмскулСкачать
Задачи на комбинаторику #5Скачать
Решение задачи на размещения, перестановки и сочетанияСкачать
Алгебра 9 класс Макарычев Ч 20 п 33Скачать
Комбинаторика: перестановки, размещения, сочетания. ВероятностьСкачать
9 класс, 2 урок, Множества и операции над нимиСкачать
Теория вероятностей задание В10 21 aviСкачать
КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать
Размещения без повторенийСкачать
