О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Доказательство теоремы синусов
- Доказательство следствия из теоремы синусов
- Теорема о вписанном в окружность угле
- Примеры решения задач
- Запоминаем
- Формулы вычисления площади произвольного четырёхугольника
- Определения и соглашения
- Нахождение площади четырёхугольника различными способами и методами
- Заключение
- Видео
- Четырехугольники
- теория по математике 📈 планиметрия
- Выпуклый четырехугольник
- Виды и свойства выпуклых четырехугольников
- Прямоугольник
- Квадрат
- Параллелограмм
- Трапеция
- Виды трапеций
- Средняя линия трапеции
- Видео
Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Доказательство теоремы синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
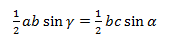
На b сокращаем, синусы переносим в знаменатели:
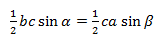
bc sinα = ca sinβ
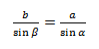
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
- Стороны треугольника, если даны два угла и одна сторона.
- Углы треугольника, если даны две стороны и один прилежащий угол.
Видео:ОГЭ как найти тангенс угла, если нет треугольника #математика #огэ #огэматематика #геометрияСкачать

Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° — α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° — α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° — α) = 2R sinα
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
- sin120° = sin(180° — 60°) = sin60° = 3/√2;
- sin150° = sin(180° — 30°) = sin30° = 1/2;
- sin135° = sin(180° — 45°) = sin45° = 2/√2.
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.
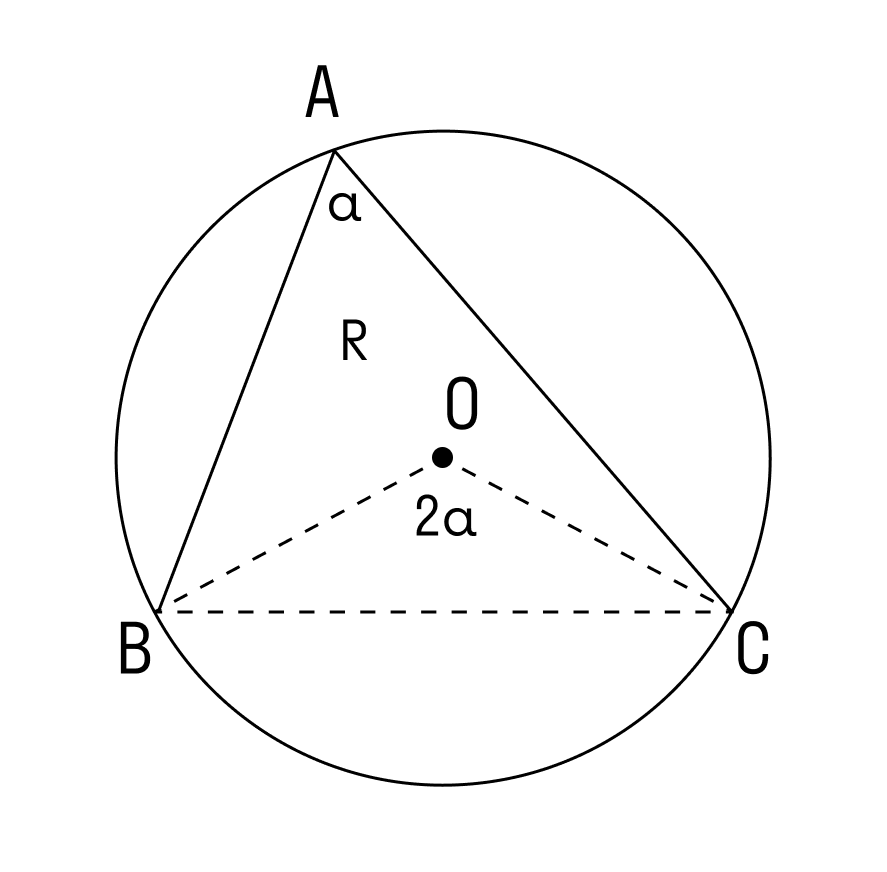
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:
Следствие 1 из теоремы о вписанном в окружность угле
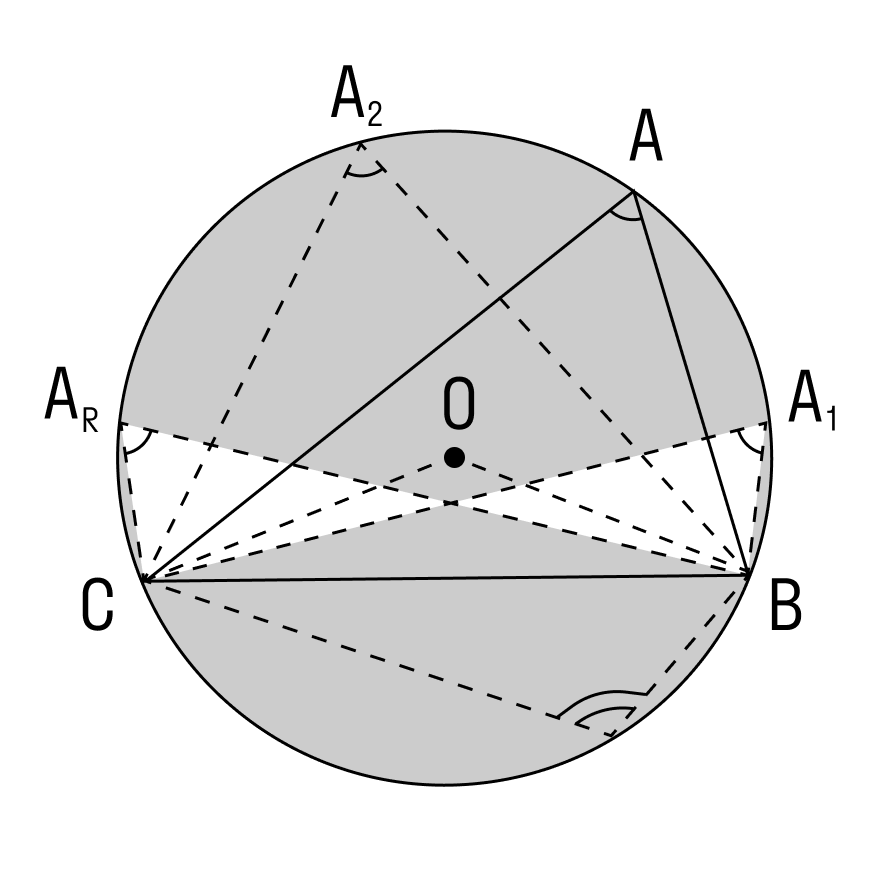
Вписанные углы, опирающиеся на одну дугу, равны.
∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:
На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
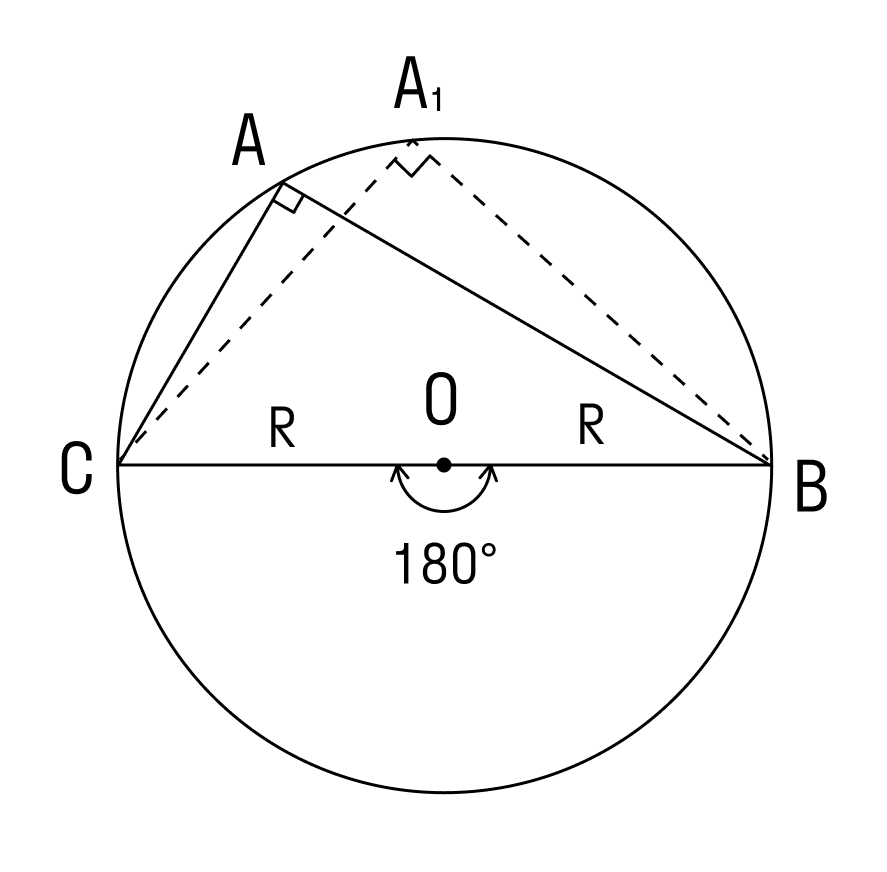
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.
ВС — диаметр описанной окружности, следовательно ∠COB = 180°.
Следствие 3 из теоремы о вписанном в окружность угле
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:
Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.
Следовательно: α + γ = 180°.
Поэтому: ∠A + ∠C = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
sinγ = sin(180° — α)
Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα
Видео:Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать

Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
- Согласно теореме о сумме углов треугольника:
∠B = 180° — 45° — 15° = 120°
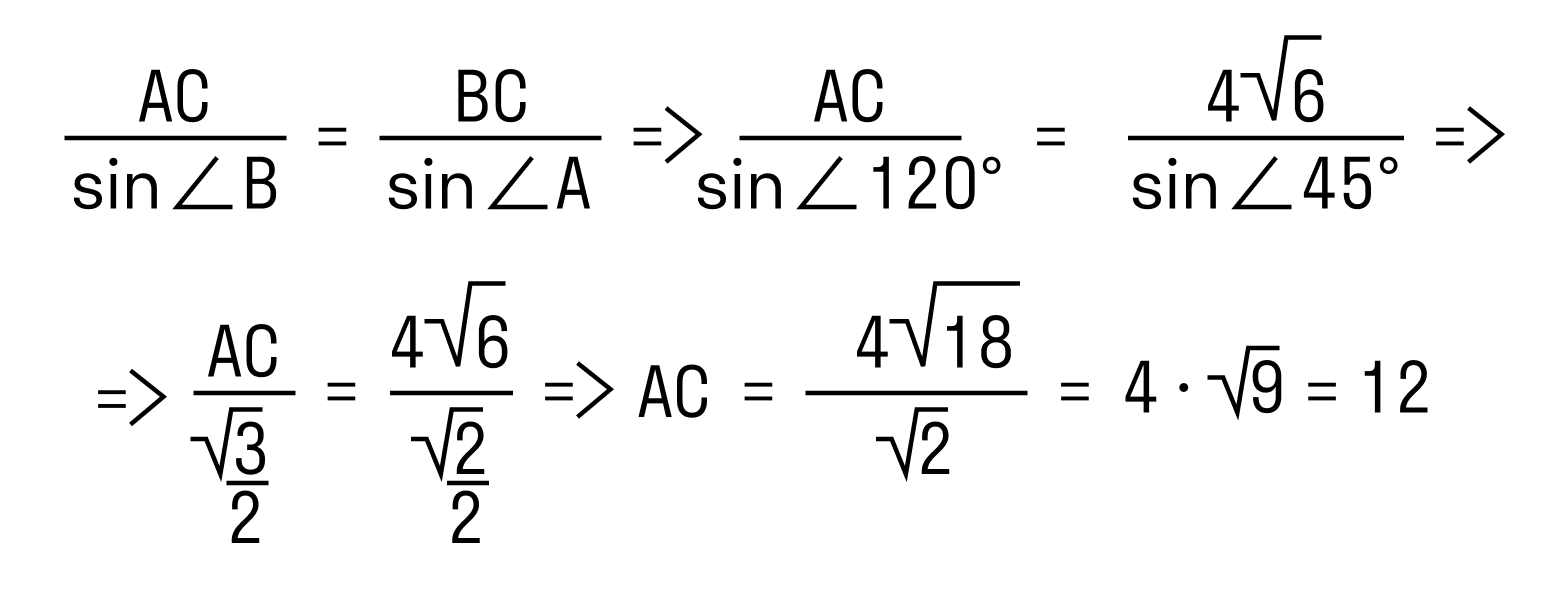
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Значит x = sin (4/5) ≈ 53,1°.
Ответ: угол составляет примерно 53,1°.
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
>
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры |
Решение
Для решения 1 задачи работаем с текстом и планом одновременно:
при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.
Итак, получили следующее:
1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.
Заполняем нашу таблицу:
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры | 3 | 5 | 1 | 7 |
Записываем ответ: 3517
Задание №2
Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?
Решение
Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).
Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».
Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.
Задание №3
Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение
Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.
Задание №4
Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.
Решение
Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).
Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м
Задание №5
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.
| Номер магазина | Расход краски | Масса краски в одной банке | Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,25 кг/кв.м | 6 кг | 3000 руб. | 500 руб. |
| 2 | 0,4 кг/кв.м | 5 кг | 1900 руб. | 800 руб. |
Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?
Решение
Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:
1 магазин: 232х0,25=58 кг
2 магазин: 232х0,4=92,8 кг
Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:
1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)
2 магазин: 92,8:5=18,56; значит надо 19 банок.
Вычислим стоимость краски в каждом магазине плюс доставка:
1 магазин: 10х3000+500=30500 руб.
2 магазин: 19х1900+800=36900 руб.
Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
🎦 Видео
Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Вписанный в окружность четырёхугольник.Скачать

ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать

🔴 Найдите sinx, если cosx=-√15/4 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 5 | ШКОЛА ПИФАГОРАСкачать

№366. Найдите стороны четырёхугольника, если его периметр равен 8 смСкачать

Спидран: Как запомнить таблицу синусов и косинусов за 1 минуту? Евгений ДолжкевичСкачать

Задача, которую боятсяСкачать



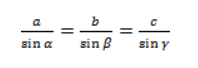
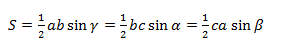
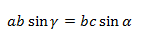
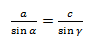
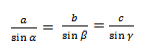

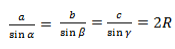

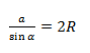


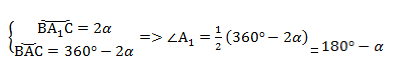

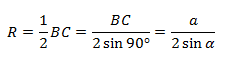
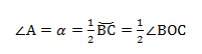
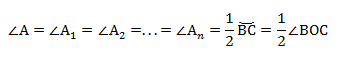
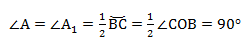

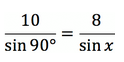
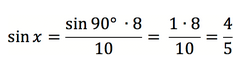



 Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.

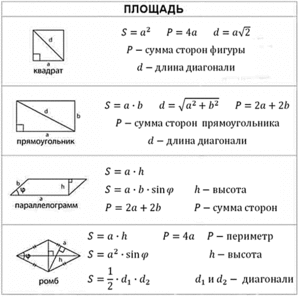



 Определение
Определение

 На рисунке видно, что углы А, В, C и D прямые, то есть равны 90 градусов. Свойства прямоугольника, его периметр и площадь
На рисунке видно, что углы А, В, C и D прямые, то есть равны 90 градусов. Свойства прямоугольника, его периметр и площадь 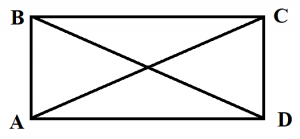
 Свойства квадрата
Свойства квадрата