Неверные признаки равенства треугольников (2 видео)

«Нестандартные признаки равенства треугольников»

Материал исследовательской работы может использоваться для кружков по геометрии в 7 классе

Содержание

Скачать:
Предварительный просмотр:
Признаки равенства треугольников
Первый признак равенства треугольников
Второй признак равенства треугольников
Третий признак равенства треугольников
«Новые» признаки равенства треугольников
📹 Видео

Видео:Признаки равенства треугольников. 7 класс.Скачать

Скачать:

Вложение	Размер
podgornyy_m.docx	257.55 КБ

Видео:Первый признак равенства треугольников. 7 класс.Скачать

Предварительный просмотр:

МБУ ДО города Ростова-на-Дону «Дворец творчества детей и молодежи»

Донская академия наук юных исследователей им. Ю. А. Жданова

Тема: «Нестандартные теоремы о равенстве треугольников»

Подгорный Максим, 7 кл.,

г. Сальск, Ростовская область

Олейникова Людмила Александровна,

г. Сальск, Ростовская область

Признаки равенства треугольников…………………………………………… 4

Нестандартные признаки равенства треугольников………………………….7

Треугольник одна из основных фигур в планиметрии. Я много слышал от старшеклассников, что при подготовке к ЕГЭ им часто приходится доказывать равенство треугольников. И оказывается недостаточным знание основных признаков. Мне захотелось узнать, а можно ли доказать равенство треугольников по другим параметрам . В учебнике геометрии, по которому обучаются ученики нашей школы ( авторы Л.С.Атанасян, В.Ф.Бутузов и др. Геометрия 7-9) рассматриваются всего 3 признака равенства треугольников. Я просмотрел учебно-методические комплекты других авторов. Но и в них для изучения предлагаются только три известные теоремы.

Возможно, ли сформулировать, кроме трех известных, другие признаки равенства треугольников?

Чтобы убедиться в том, что ответ на этот вопрос волнует не только меня, я провел социологический опрос среди учащихся 7-11 классов см. приложение 1 ).

Мои предположения подтвердились. Большенство учеников знают только три признака равенства треугольников.

Таким образом, целью моего исследования стало отыскание новых признаков равенства треугольников.

ΘИзучить литературу по исследуемой теме.

ΘУточнить количество признаков равенства треугольников.

ΘПродемонстрировать своим одноклассникам и учащимся нашей школы существование других признаков равенства треугольников и возможности их доказательства.

Изучение признаков равенства треугольников.

Предмет исследования . Треугольник, как одна из основных фигур в планиметрии.

Метод исследования: Теоретический ( изучение, анализ и синтез),системно-поисковый, практический (доказательство теорем ).

Треугольник является одной из центральных фигур всей геометрии.

При решении задач используют его самые разнообразные свойства.

Свойства треугольника широко применяют на практике: в архитектуре; при разработке чертежа здания, при планировке будущих квартир; в промышленности, при проектировании различных деталей, при изготовлении стройматериалов, при строительстве морских и авиа судов; в навигации для проложения правильного и максимально точного маршрута; в астрологии и астрономии треугольник является очень значимой фигурой; треугольники делают надежными конструкции высоковольтных линий электропередач и железнодорожных мостов.

Кроме того, много других сфер, где применяются различные свойства треугольника: начиная игру в бильярд, необходимо расположить шары в виде треугольника, для этого используют специальное приспособление; расстановка кеглей в игре Боулинг тоже в виде равностороннего треугольника; для составления красивых паркетов используются треугольники; устройство треугольника Паскаля: каждое число равно сумме двух расположенных над ним чисел (обвести треугольником три числа). Все элементарно, но сколько в этом таится чудес! Треугольник Паскаля компьютер перевёл на язык цвета.

Тему треугольника можно продолжать неограниченно.

Каких только треугольников нет на свете!

Существуют также переносные значения данной фигуры: например, правило «золотого треугольника» основано на психологии покупателя – найдя нужный ему товар, покупатель устремляется в кассу. Задача продавцов – заставить его задержаться в магазине подольше, расположив нужный покупателю товар в вершинах воображаемого треугольника, то есть «заякорить» покупателя. Чем больше площадь треугольника, тем более удачным можно назвать планировку магазина. В продуктовом магазине этими товарами-якорями являются гастрономия, молочная продукция, хлеб. Задняя торцевая стена торгового зала является вторым местом по значимости и именно там целесообразнее всего располагать товары-якоря – именно для того, что бы заставить покупателя пройти весь периметр магазина.

Широко известный Бермудский треугольник – это район в Атлантическом океане, в котором происходят якобы таинственные исчезновения морских и воздушных судов. Район ограничен линиями от Флориды к Бермудским островам, далее к Пуэрто-Рико и назад к Флориде через Багамы.

Поэтому изучение треугольника и всех его свойств – очень актуальная тема.

Цель данной работы – рассказать о признаках равенства треугольников, что является одним из важнейших их свойств.

Признаки равенства треугольников — это теоремы, на основании которых можно доказать, что некоторые треугольники равны.

В геометрии используются три признака равенства треугольников.

Данная тема практически изучена, так как на сегодняшний день существуют три признака равенства треугольников, доказываемых с помощью соответствующих теорем.

В глубокой древности вместе с астрономией появилась наука – тригонометрия. Слово «тригонометрия» произведено от греческих «треугольник» и «меряю». Буквальное значение – «наука об измерении треугольников».

С помощью натянутых веревок длиной 3, 4 и 5 единиц египетские жрецы получали прямые углы при возведении храмов и т.п.

Искусство изображать предметы на плоскости с Древних времён привлекает к себе внимание человека, люди рисовали на скалах, стенах, сосудах и прочих предметах быта, различные орнаменты, растения, животных. Люди стремились к тому, чтобы изображение правильно отображало естественную форму предмета.

Учение о подобии фигур на основе теории отношений и пропорций было создано в Древней Греции в 5-4 веках до нашей эры и существует и развивается до сих пор. Например, очень много детских игрушек подобным предметам взрослого мира, обувь и одежда одного фасона выпускается различных размеров. Эти примеры можно продолжать и дальше. В конце концов, все люди подобны друг другу и как утверждает Библия, создал их бог по своему образу и подобию.

Признаки равенства треугольников имели издавна важнейшее значение в геометрии, так как доказательства многочисленных теорем сводилось к доказательству равенства тех или иных треугольников. Доказательством признаков равенства треугольников занимались еще пифагорейцы. По словам Прокла, Евдем Родосский приписывает Фалесу Милетскому доказательство о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников).

Эту теорему Фалес использовал для определения расстояния от берега до морских кораблей. Каким способом пользовался при этом Фалес, точно не известно.

Признаки равенства треугольников.

Начнем с определения. Треугольники АВС и А1В1С1 называются равными, если их можно совместить наложением.

Треугольник состоит из шести элементов: трех углов и трех сторон.

При этом возникает вопрос : » Какое наименьшее количество элементов треугольника нужно взять для установления равенства двух треугольников ?»

Мы не сможем установить равенство двух треугольников по одному элементу, потому что неизвестно :»Будут ли равны остальные элементы ?»

Так же невозможно установить равенство двух треугольников, используя два элемента по причине нехватки информации для установления равенства.

Возможно установление равенства двух треугольников, используя три элемента. Но при этом возникает вопрос : «Какие именно три элемента нужно назвать, для установления равенства треугольников ?»

При изучении этого вопроса , я просмотрел школьные учебники геометрии различных авторов, а также словари и справочники. В учебниках за седьмой класс предложены к изучению только три признака равенства треугольников.

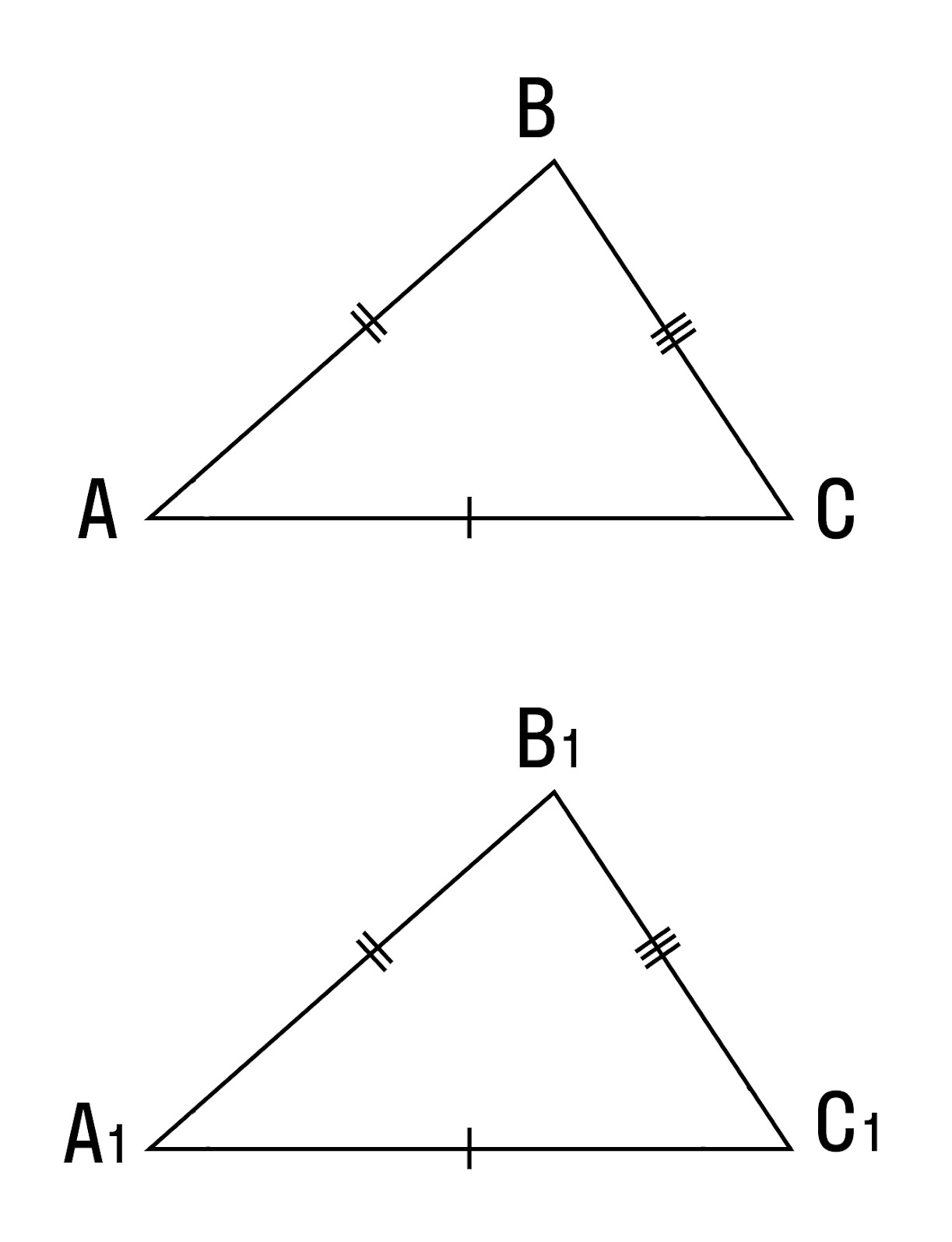
Θ1 Признак : Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны . рис.1

Доказательство. Рассмотрим треугольники ABC и A 1 B 1 C 1 , (рис. 1) у которых АВ = A 1 B 1 , АС = A 1 C 1 ∠ А = ∠ А 1 . Докажем, что ΔABC = ΔA 1 B 1 C 1 .

Так как ∠А = ∠А 1 , то треугольник ABC можно наложить на треугольник А 1 В 1 С 1 так, что вершина А совместится с вершиной А 1 , а стороны АВ и АС наложатся соответственно на лучи А 1 В 1 и A 1 C 1 . Поскольку АВ = A 1 B 1 , АС = А 1 С 1 , то сторона АВ совместится со стороной А 1 В 1 а сторона АС — со стороной А 1 C 1 ; в частности, совместятся точки В и В 1 , С и C 1 . Следовательно, совместятся стороны ВС и В 1 С 1 . Итак, треугольники ABC и А 1 В 1 С 1 полностью совместятся, значит, они равны.

А вот как в Древнем Египте применили первый признак равенства треугольников ( по двум сторонам и углу между ними), создателем его также считается Фалес Милетский, для измерения высоты пирамиды: представим, что мы стоим перед огромной пирамидой, как же измерить её высоту? Ведь к ней не приложишь измерительные приборы! И тут на помощь Фалесу Милетскому приходит первый признак равенства треугольников: он подождал пока тень его точно совпадёт с его ростом, применил теорему, получилось, что высота пирамиды равна её тени (рис. 2).

Θ2 Признак : Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Доказательство: Если в △АВС и △А 1 В 1 С 1 будут иметь место следующие равенства AB=А 1 В 1 , ∠BAC=∠B 1 A 1 C 1 , ∠АВС= ∠А 1 В 1 С 1 . Наложим друг на друга треугольники А 1 В 1 С 1 и АВС таким образом, чтобы совпали равные стороны AB и А 1 В 1 и углы, которые к ним прилегают. Как и в уже рассмотренном предыдущем примере, если это необходимо, треугольник А 1 В 1 С 1 можно «перевернуть и приложить обратной стороной». Треугольники совпадут, следовательно, они могут считаться равными.

Θ3 Признак : Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. Доказательство:Пусть для △ABC и △A 1 B 1 C 1 справедливы равенства А 1 В 1 =АВ, В 1 С 1 =ВС, С 1 А 1 =СА. Переместим треугольник А 1 В 1 С 1 таким образом, что сторона А 1 В 1 совпадет со стороной АВ, и вершины B 1 и B, A 1 и A, совпадут. Возьмем окружность с центром в A и радиусом AC, и вторую окружность с центром B и радиусом BC. Эти окружности пересекутся в двух симметричных относительно отрезка AB точках: точкой C и точкой C 2 . Значит, C1 после переноса треугольника A1B1C1 должна совпасть или с точками C, или с C2. Любом случае, это будет означать равенство △ABC=△A 1 B 1 C 1 , так как треугольники △ABC=△ABC 2 равны (ведь эти треугольники являются симметричными относительно отрезка AB .

Это свойство – жесткость треугольника – широко используется на практике. Так, чтобы закрепить столб в вертикальном положении, к нему ставят подпорку; такой же принцип используется при установке кронштейна.

Свойство жесткости треугольника широко используют в практике при строительстве железных конструкций.

Из третьего признака равенства треугольников следует, что треугольник — жёсткая фигура. Потому, что: можно представим себе две рейки, у которых два конца скреплены гвоздем. Такая конструкция не является жёсткой, однако, сдвигая или раздвигая свободные концы реек, мы можем менять угол между ними. Теперь возьмем ещё одну рейку и скрепим её концы со свободными концами первых двух реек . Полученная конструкция — треугольник — будет уже жёсткой. В ней нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол. Действительно, если бы это удалось, то мы получили бы новый треугольник, не равный исходному. Но это невозможно, так как новый треугольник должен быть равен исходному по третьему

В справочнике по элементарной математике М. Я. Выгодского я нашел еще один признак.

Θ4 Признак : Если две стороны и угол, лежащий против большей из них одного треугольника соответственно равны двум сторонам и углу, лежащему против большей из них другого треугольника, то такие треугольники равны.

Докажу этот признак.

Дано : ΔABC , ΔA1B1C1 , AB=A1B1,AC=A1C1, ∠ B= ∠ B1

Расположим треугольники так , как на рисунке 1 . Соединим B и B1, тогда ΔАВВ1

-равнобедренный , значит ∠ 1= ∠ 2. ∠ 3= ∠ 4 как остатки равных углов .

Получим ΔВСВ1- равнобедренный, отсюда ВС=В1С1. ΔАВС = ΔА1В1С1 по трем сторонам.

Также в школьном курсе рассматриваются 4 признака равенства прямоугольных треугольников :

Θ1 . Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.

Θ2 . Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого , то такие треугольники равны.

Θ3 . Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.

Θ4 . Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.

Я решил теоретическую базу по признакам равенства треугольников , довавив к сторонам и углам , используемым в класических признаках равенства треугольников , другие компоненты : биссектрису , медиану и высоту.

Нестандартные признаки равества треугольников.

1) По двум сторонам и высоте проведенной к одной из них .

Дано: AB=A1B1 , BC=B1C1 , AK=A1K1 ,

Доказать : ΔABC= ΔA1B1C1 .

Доказательство : ΔABK=ΔA1B1K1 по гипотенузе и катету , тогда ∠ B= ∠ B1 и получим ΔABC= ΔA1B1C1 по первому признаку .

2) По двум сторонам и медиане , проведенной к одной из них

Дано: AB=A1B1 , BC=B1C1 , AK=A1K1 , AK и A1K1 — медианы.

Доказать : ΔABC= ΔA1B1C1 .

Доказательство :ΔABK=ΔA1B1K1 по трем сторонам , значит ∠ B= ∠ B1 и ΔABC= ΔA1B1C1 по первому признаку.

3) По двум сторонам и высоте , проведенной из третьего угла.

Дано: ∠ B= ∠ B1 , ∠ C= ∠ C1 , AK=A1K1 .

Доказать : ΔABC= ΔA1B1C1 .

Доказательство : ΔABK=ΔA1B1K1 по катету и острому углу , значит BK=B1K1 ,

ΔACK=ΔA1C1K1 по катету и острому углу , значит KC=K1C1 , а следовательно BC=B1C1 , а ΔABC= ΔA1B1C1 по второму признаку.

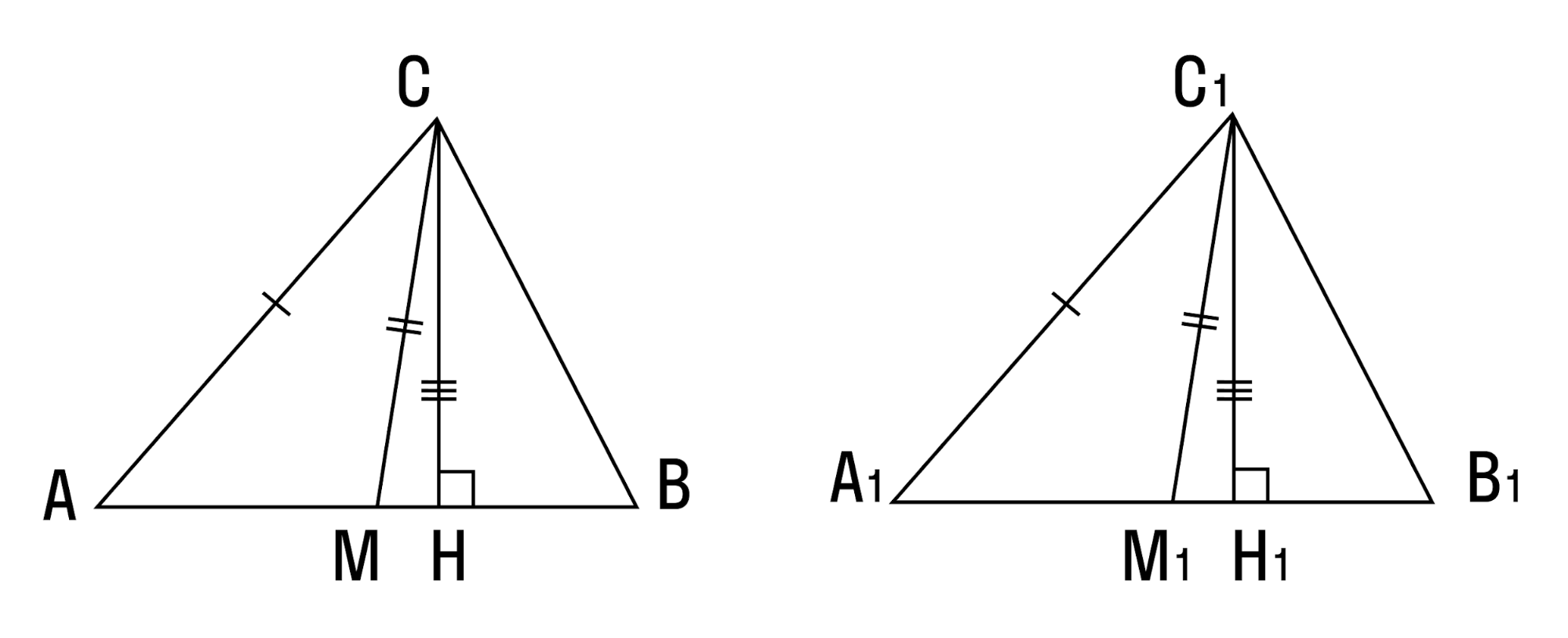
4)По стороне и двум высотам , проведенным из углов , прилежащих к этой стороне .

Дано: АС=А1С1, СМ=С1М1, АК=А1К1.

Доказать : ΔСC= ΔA1B1C1 .

Доказательство: ΔAМC= ΔA1М1C1 по катету и гипотенузе , значит ∠ А= ∠ А1 , а ΔAКC= ΔA1К1C1 по катету и гипотенузе , значит ∠ С= ∠ С1 .

Итак , ΔABC= ΔA1B1C1 по второму признаку .

5)По двум сторонам и высоте , проведеннойк третьей стороне .

Доказать : ΔABC= ΔA1B1C1 .

Доказательство: ΔABK=ΔA1B1K1 по гипотенузе и катету , значит AK=A1K1,

ΔBКC= ΔB1К1C1 по катету и гипотенузе, значит KC=K1C1 .

Итак ,ΔABC= ΔA1B1C1 по трем сторонам.

6)По стороне , одному из углов , прилежайщих к этой стороне и биссектрисе из этого угла.

Дано: АС=А1С1, АК=А1К1, ∠ А ∠ А1 .

Доказать : ΔABC= ΔA1B1C1 .

Доказательство: ΔКАС=ΔК1А1С1 по первому признаку , значит ∠ С= ∠ С1 ,

ΔABC= ΔA1B1C1 по второму признаку.

7) По двум высотам и углу , из которого провдена одна из высот .

Дано : СМ=С1М1, АК=А1К1, ∠ А ∠ А1 .

Доказать : ΔABC= ΔA1B1C1 .

Доказательство : ΔAМC= ΔA1М1C1 по катету и острому углу,ΔКАС=ΔК1А1С1 по катету и гипотенузе ,ΔABC= ΔA1B1C1 по второму признаку.

В ходе исследования я выяснил, что помимо трех основных признаков равенства треугольников возможно указать немало других. Я сформулировал и доказал равенство треугольников по медиане, высоте, биссектрисе треугольника в сочетании со сторонами и углами треугольника, придерживаясь наличия трех элементов. Теперь я могу рассказать учащимся нашей школы, что существуют другие признаки равенства треугольников. Это позволит выпускникам школы применить результаты моих исследований при подготовке к ОГЭ и ЕГЭ и легко решать геометрические задачи на применение этих признаков.

Результат моего исследования : Доказаны несколько признаков равенства треугольников, не изучаемых в школьном курсе геометрии.

Выгодский М.Я. Справочник по элементарной математике.
Геометрия. 7-9 классы: учеб. Для общеобразоват. учреждений/Л.С.Атанасян, В.Ф.Бутузов, С.Б. Кадомцев и др. – 19-е изд. – М. : Просвещение, 2009.
Погорелов А. В. Геометрия: Учеб. Для 7-9 кл. общеобразоват. Учреждений. – 3-е издание. – М.: Просвещение, 2002.
. Энциклопедия «Аванта» по математике, Москва, 2004 г.
2. «Википедия» — свободная энциклопедия.
3. Глейзер Г.И. «История математики в школе», Москва, Просвещение, 1982 г.
4. Гусева Т.М. Признаки подобия треугольников.- Москва, Первое сентября, приложение «Математика», 1999 г., №28
5. Погорелов А.В. «Геометрия 7-9 классы», Москва, Просвещение, 2003 г.

1.Как вы считаете, сколько существует признаков равенства треугольников?

А) 3 Б) более трех В) меньше трех

2. Хотели бы вы узнать новые признаки равенства треугольников?

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Признаки равенства треугольников

О чем эта статья:

Видео:Первый признак равенства треугольников | Теорема + доказательствоСкачать

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Видео:7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Второй признак равенства треугольников

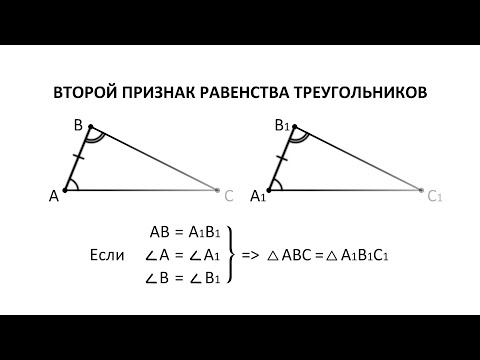
Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Видео:Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

Третий признак равенства треугольников

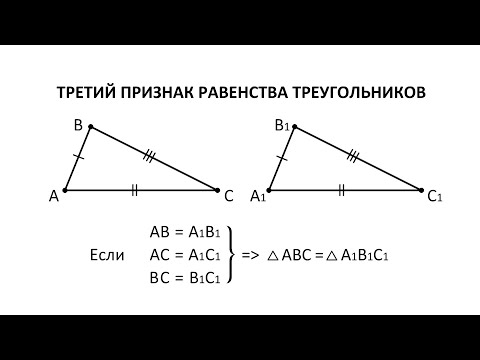
Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

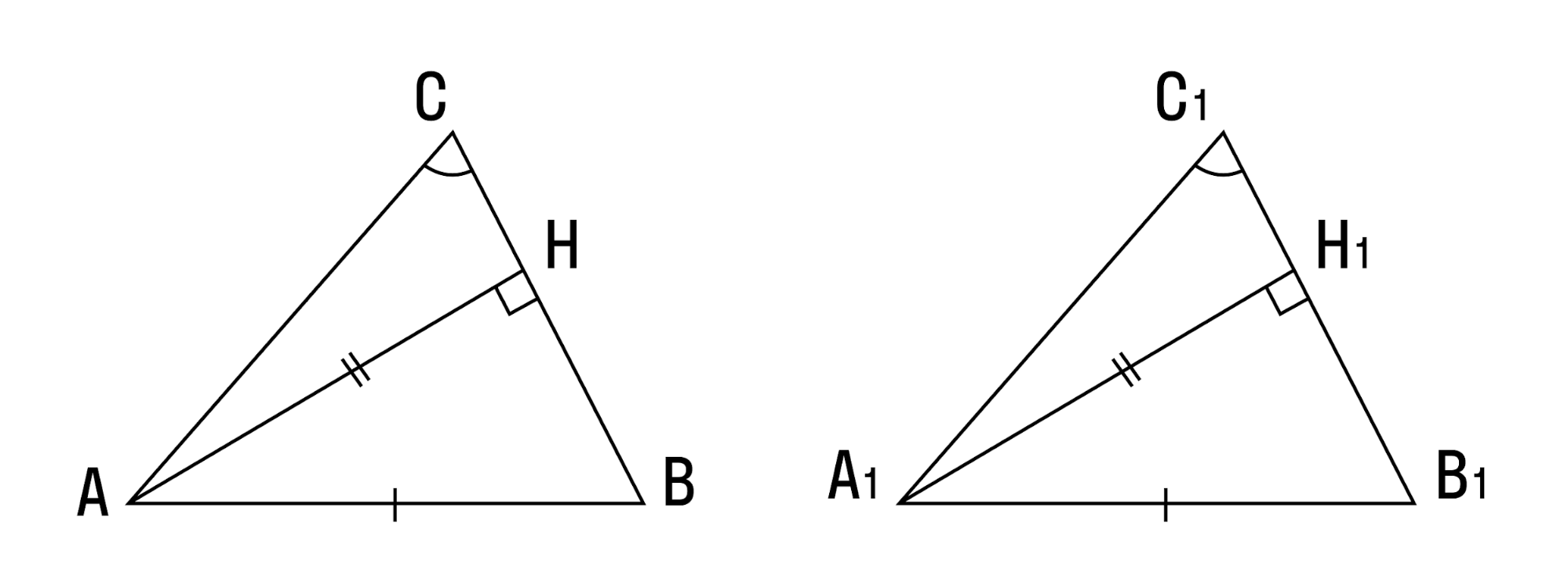
Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
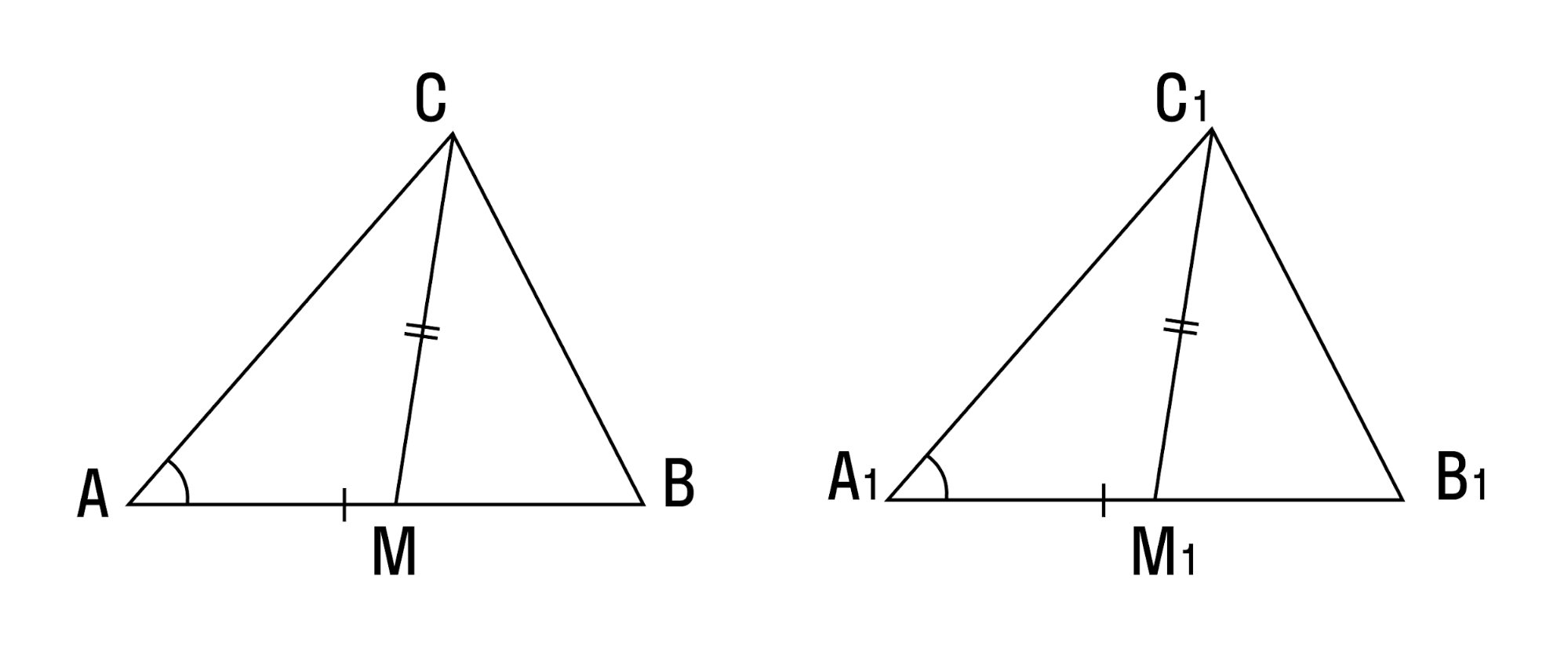
Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Видео:Второй признак равенства треугольников. 7 класс.Скачать

«Новые» признаки равенства треугольников

Международная научно-практическая конференция «Первые шаги в науку»

«Новые» признаки равенства треугольников

9б класс МБОУ «Брянский городской
лицей №2 имени »

Руководитель: учитель математики

Брянск 2013

2. Создание каталога базовых задач на построение с помощью циркуля и линейки

3. Сопоставление изученных признаков равенства треугольников и задач на построение треугольников. Отыскание нового метода доказательства признаков равенства треугольников

4. Доказательство новых признаков равенства треугольников

5. Обобщение полученных результатов

6. Применение новых признаков равенства треугольников при решении задач

«Если две стороны и угол между ними одного треугольника…..». Заученные, как таблица умножения, признаки равенства треугольников. Сотни раз мы цитировали и применяли их при решении задач. Казалось бы, что может быть проще? Мы знаем об этом все!

Однако до сих пор остались вопросы, ответы на которые не дают нам покоя. Метод наложения, используемый для доказательства первого признака равенства, показался нам несколько искусственным. Не потому ли мы никогда не использовали его в решении задач? Почему так мало признаков равенства треугольников? В 8 классе строили треугольники по все тем же двум сторонам и углу между ними. Случайность? Но в математике нет случайных совпадений.

Возможно, обнаружив связь между решением задач на построение треугольников и признаками равенства, мы получим новый метод доказательства ПРТ. «Вооружившись» им мы сможем доказать другие признаки равенства треугольников. Мы уверены, что их гораздо больше, чем 3!

Чтобы убедиться в том, что ответы на эти вопросы волнуют не только нас, мы провели социологический опрос среди учащихся и учителей лицея (см. приложение 3).

Наши предположения подтвердились. Большинство учеников знают только 3 признака равенства треугольников. Метод наложения не пользуется большой популярностью. Задачи на построение также не кажутся интересной темой в геометрии. А этап исследования многие вообще считают лишним.

Таким образом, целью нашего исследования стало отыскание более понятного нам метода доказательства признаков равенства треугольников и новых признаков равенства треугольников.

Крайне важно было дополнить перечень простейших задач на построение, изученных в седьмом классе, другими элементарными построениями, которые мы проходили в курсе восьмого и девятого класса. Всего получилось 12 базовых построений (см. приложение 1). В ходе дальнейшего исследования мы будем неоднократно обращаться к этому перечню.

Нужно отметить, что все задачи мы решали по алгоритму: дано-построить-анализ-построение-доказать-доказательство-исследование. Для простых задач и задач, решение которых известно, этап анализа мы опускали.

Больше всего внимание уделялось последнему этапу – исследованию, именно он дал нам возможность отыскать новый метод доказательства.

Чертежи было решено выполнять в программе Paint, поэтому возникла необходимость заранее научиться работать в ней.

II. Создание каталога базовых задач на построение с помощью циркуля и линейки

Большая часть нашей работы заключается в решении задач на построение треугольников, поэтому на первом этапе работы мы составили список простейших построений. Это позволило сделать решение задач более коротким и красивым.

Все задачи мы решали по плану: дано – построить – построение – доказать – доказательство — исследование. Особое значение уделялось этапу исследования.

Базовые задачи на построение решались в различных разделах геометрии 7 и 8 класса. Мы их собрали в единый каталог.

1) Построение отрезка, равного данному;

2) Построение угла, равного данному;

3) Построение биссектрисы угла;

4) Построение середины отрезка;

5) Построение перпендикуляра через точку лежащую/не лежащую на данной прямой;

6) Построение прямой, параллельной данной;

7) Построение третьего угла, по двум известным;

8) Построение касательной к окружности, через точку не лежащую на данной окружности;

9) Деление отрезка в заданном отношении;

10) Деление отрезка в заданном отношении отрезков;

11) Деление отрезка на n равных отрезков.

Подробное решение этих задач представлено в приложении 1.

III. Сопоставление изученных признаков равенства треугольников и задач на построение треугольников. Отыскание нового метода доказательства признаков равенства треугольников.

Для поиска нового метода доказательства ПРТ мы сопоставили условие первого ПРТ с условием одной из задач на построение. Они оказались одинаковыми и мы предположили, что это не случайно и решение задачи на построение приведет нас к нахождению нового метода доказательства.

Построение треугольника по двум сторонам и углу между ними

Вывод: В силу единственности построения, все треугольники, у которых две стороны и угол между ними соответственно равны заданным элементам, равны.

Построение треугольника по стороне и двум прилежащим к ней углам

Вывод: В силу единственности построения, все треугольники, у которых сторона и прилежащие к ней углы соответственно равны заданным элементам, равны.

Построение треугольника по трем сторонам

Вывод: В силу единственности построения, все треугольники, у которых три стороны соответственно равны заданным элементам, равны.

Итак, если треугольник, построенный по заданным элементам единственный, то треугольники, элементы которых соответственно равны заданным, равны построенному.

Таким образом, если по трем элементам треугольник построен единственный, то соответственное равенство этих элементов у двух треугольников означает, что треугольники равны.

IV. Поиск новых признаков равенства, используя новый метод доказательства ПРТ.

Теперь «новый» метод был, как говорится, у нас в кармане. Открытым оставался один вопрос: сколько существует признаков равенства треугольников?

Используя новый метод доказательства, мы принялись решать задачи на построение треугольников. Наборы элементов выбирались не случайно, мы использовали пособие , содержащие только условие задач на построение треугольников. Задачи мы решали самостоятельно.

Большинство задач мы брали из книги «Это должен знать каждый матшкольник», где представлены только условия, а задачи решались самостоятельно [2].

Вот одна из задач, решение которой привело нас к новому ПРТ.

ПРТ, доказанный в решении этой задачи, звучит так: «Если две стороны и медиана, проведенная к третьей, одного треугольника соответственно равны двум сторонам и медиане, проведенной к третьей, другого треугольника, то эти треугольники равны.»

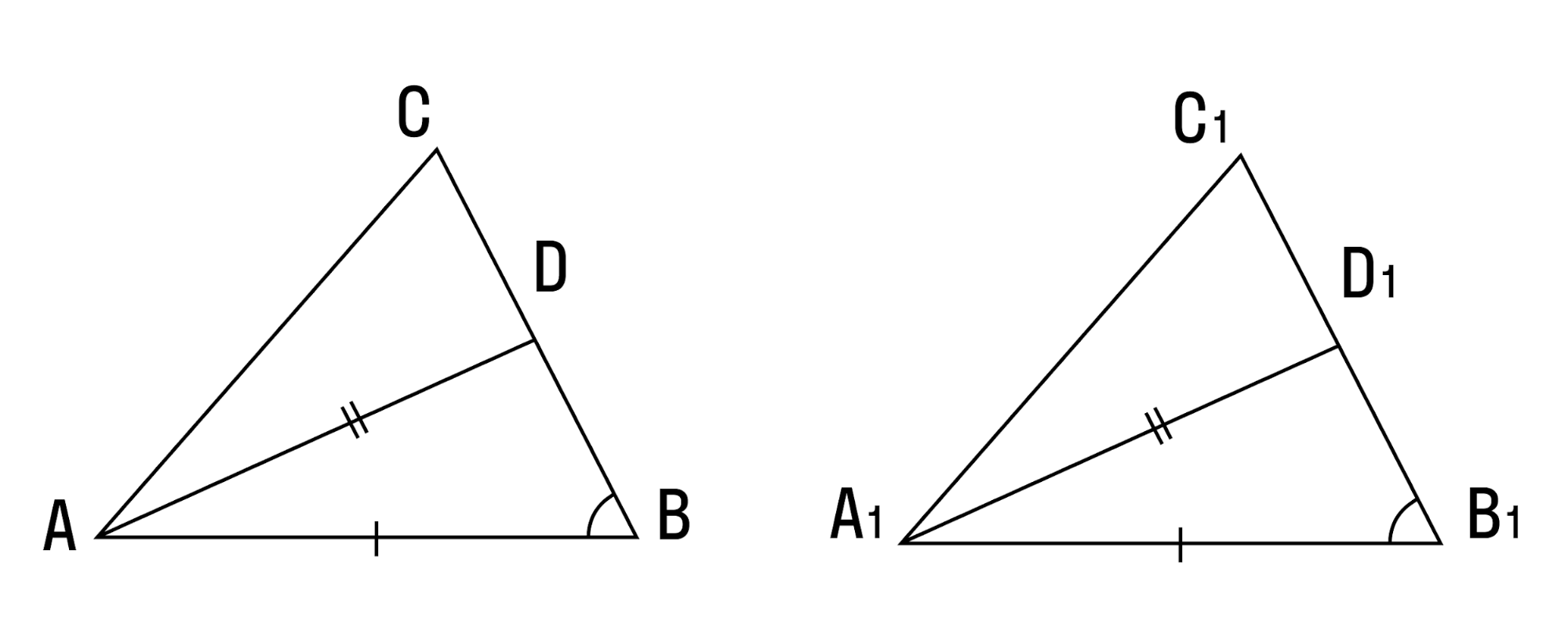
Но не все задачи решались так просто. Например, задача на построение по двум сторонам и углу, прилежащему к одной из сторон, нового признака равенства не дала. Однако стоило нам немного изменить условие, и был получен еще один ПРТ. Решение этой задачи было особенно важно для нас, потому что ее условие мы придумывали сами.

Построение треугольника по двум сторонам и углу, прилежащему к одной из этих сторон

После решения этой задачи, мы обратились к интернет — ресурсам и узнали, что это утверждение иногда называют 4 признаком равенства треугольников. Его доказательство приведено профессором МГУ , на сайте «Математика в школе», создателем которого является факультет педагогического образования МГУ имени . Это доказательство принципиально отличается от предложенного нами [3]. Полное доказательство вы найдете http://www. school. *****///.

V. Обобщение полученных результатов

Итак, мы нашли новый метод доказательства ПРТ. Если по трем элементам треугольник построен единственный, то соответственное равенство этих элементов у двух треугольников означает, что треугольники равны.

Этот метод позволил создать новые признаки равенства треугольников:

4 ПРТ. По двум сторонам и углу, противолежащему к большей из них.

5 ПРТ. По стороне, противолежащему углу и высоте, проведенной из вершины данного угла.

6 ПРТ. По двум углам и высоте, проведенной из вершины третьего.

7 ПРТ. По двум углам и периметру (два варианта решения).

8 ПРТ. По двум сторонам и медиане, проведенной к третьей.

9 ПРТ. По трем медианам.

10 ПРТ. По двум углам и стороне, прилежащей к одному из них.

Подробное доказательство каждого из них представлено в приложении 3.

VI. Применение новых признаков равенства треугольников при решении задач

Возможно, кого-то мы еще не до конца убедили в важности нашего исследования. Конечно, любое исследование важно само по себе, ведь это изучение проблемы, поиск ответов на вопросы… Но наша работа имеет более определенное практическое значение, нежели просто интерес. Ведь множество задач по геометрии требует знания признаков равенства треугольников, а чем больше признаков, тем разнообразнее решения.

В учебнике «Геометрия 7-9» Атанасяна [1] приведена задача повышенной сложности № 000*

Приведем ее решение двумя способами.

1 способ. «Удвоение медианы»

MD=AM, DÎпрямой АМ

M1D1=A1M1, D1Îпрямой А1M1

2) AM=MD и BM=MC => ABCD-параллелограмм (по признаку)

3) A1M1=M1D1 и B1M1=M1C1 => A1B1C1D1-параллелограмм (по признаку)

4) DАВС=DА1В1С1, т. к.: АВ=А1В1(по условию)

B1D1=A1C1=A1C1=B1D1 (по свойству сторон параллелограмма)

5) Из равенства DАВD и DА1В1D1 следует равенство углов ÐАВD=ÐА1В1D1 => ÐВАС=180°-ÐАВD=180°-ÐА1В1D1 =ÐВ1А1С1

6) Рассмотрим DАВС и DА1В1С1:

АВ=А1В1; АС=А1С1, по условию; ÐА=ÐА1, по доказанному =>DА1В1С1=DА1В1С1 по двум сторонам и углу между ними.

2 способ. С применением 7ПРТ

По условию АВ=А1В1; АС=А1С1; АМ=А1М1. Следовательно, DАВС=DА1В1С1 по двум сторонам и медиане, проведенной к третьей (7ПРТ).

Очевидно, что 2 способ намного короче.

Подведем итоги: мы нашли метод доказательства ПРТ, отличный от метода наложения, доказали «новые» признаки равенства треугольников и решили задачи с применение этих признаков.

Также мы убедились, что в самой простой, на первый взгляд, теме может скрываться множество тайн. А задачи на построение треугольников, казавшиеся нам скучными и ненужными, стали намного интереснее, и в их актуальности больше нет никаких сомнений.

Мы нашли «инструмент», с помощью которого легко искать новые признаки равенства треугольников. Теперь, в случае необходимости, мы можем проверить, является ли набор из трех элементов признаком равенства треугольников или нет. И, несомненно, огромное удовольствие доставлял сам процесс поиска сначала нового метода доказательства ПРТ, а впоследствии открытия новых признаков равенства треугольников. Попутно мы освоили программу Paint.

Мы не можем утверждать, что были первыми, кто занимается этой проблемой. И, скорее всего, данный метод доказательства ПРТ был известен до нас. Возможно, мы что-то упустили и в «нашем» методе не все гладко. Поэтому, мы хотим представить нашу работу широкому кругу читателей. Их мнение для нас очень важно. Для этого исследование мы разместили на сайте «Виртуальный музей Лицея №2»( http://www. *****/) и завязали переписку с профессором . Мы упросили его дать отзыв о нашей работе [4].

Учащиеся и педагоги могут воспользоваться результатами нашего исследования при подготовке к урокам и экзаменам. Например, использовать расширенный список базовых задач на построение, открыть для себя новый метод доказательства ПРТ, самостоятельно доказывать признаки равенства треугольников, а также воспользоваться уже доказанными нами признаками. Очень важно, что появилась возможность сократить время на решение задач по геометрии на контрольных и экзаменах.

1. и др. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. 8-е изд.-М.: Просвещение, АО «Московсий учебник», 2010.

2. «Это должен знать каждый матшкольник». 5-е издание, стереотип.-М.:МЦНМО, 2008-56.

3. «Четвертый признак равенства треугольников», «Математика в школе» http://www. school. *****///.

4. Сайт «Виртуальный музей Лицея №2»( http://www. *****/)

Простейшие задачи на построение

Базовые построения с помощью циркуля и линейки