Сформулируйте используя законы де моргана отрицания следующих высказываний четырехугольник авсд

Вопрос по математике:

Сформулируйте, используя законы де Моргана, отрицания следующих утверждений :
а) Четырехугольник АВСД – прямоугольник или параллелограмм;
б) Число 12 – четное и делится на 3.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Видео:Законы де Моргана || Формулы де Моргана || Правило де МорганаСкачать

ТЕМА. ВЫСКАЗЫВАНИЯ С КВАНТОРОМ. ОТРИЦАНИЕ ВЫСКАЗЫВАНИЙ И ВЫСКАЗЫВАТЕЛЬНЫХ ФОРМ (С/Р)

1. Высказывания с кванторами

2. Истинность высказываний с кванторами

3. Отрицание высказываний и высказывательных форм

ПРАКТИЧЕСКАЯ РАБОТА. ВЫСКАЗЫВАНИЯ С КВАНТОРАМИ. ОТРИЦАНИЕ ВЫСКАЗЫВАНИЙ И ВЫСКАЗЫВАТЕЛЬНЫХ ФОРМ

Цель. Рассмотреть правила определения значения истинности составного высказывания и высказывательных форм с кванторами.

Теоретическая часть

Вопросы к изучению

1. Высказывания с кванторами

2. Истинность высказываний с кванторами

3. Отрицание высказываний и высказывательных форм

Основные понятия темы

Ø квантор общности;

Ø квантор существования;

Ø отрицание высказываний и высказывательных форм.

Правила

Ø нахождения множества истинности составных высказывательных форм:

Т _{А Ù В} = Т_А Ç Т _В, Т _{А Ú В} = Т_А È Т _В, Т 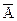= Т’_А;

Ø построения отрицания предложений различной структуры, в частности,

и Ú ; Û Ù

Û ($ х) ; Û (» х) .

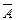
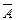
Обозначения

» х – «для всякого х», квантор общности;

$ х — «существует х такое, что …», квантор существования;

— « не А», « неверно, что А», отрицание данного предложения

Практическая часть

1. В высказывании «всякий прямоугольник является четырехугольником» выделите квантор и высказывательную форму. Переформулируйте данное высказывание, заменив слово «всякий» его синонимом.

2. В высказывании «хотя бы одно из чисел первого десятка составное» выделите квантор и высказывательную форму. Переформулируйте данное высказывание, заменив квантор «хотя бы одно» его синонимом.

3. Прочитайте следующие записи, заменив символические обозначения кванторов общности и существования их словесными выражениями: а) («х ÎR) х 2 – 1 = (х+1) (х-1); б) ($ у Î R) 5 + у =5; в) («у ÎR) у + 3 > 0; г) ($ х Î N) х +3 2 + вх +с = 0 имеет хотя бы один корень.

5. Запишите, используя символы, следующие высказывания и определите их значение истинности: а) Всякое число, умноженное на нуль, есть нуль; б) Произведение любого числа и единицы равно этому числу; в) При делении нуля на любое другое число получается нуль; г) Квадрат любого числа неотрицателен.

6. Установите, какие из нижеприведенных высказываний истинны, а какие ложны: а) Во всяком четырехугольнике диагонали равны; б) Существуют числовые выражения, значения которых нельзя найти; в) При делении на 5 некоторых натуральных чисел в остатке получается 7; г) Любое однозначное число является решением неравенства х + 2 > 1.

7. Докажите или опровергните следующие высказывания: а) Существуют уравнения, множество решений которых пусто; б) Всякое целое число является натуральным; в) Сумма любых двух четных чисел есть число четное; г) Хотя бы одно натуральное число является решением уравнения 7: х =2.

8. Данные ниже высказывания взяты из учебников математики для начальных классов. Выясните, какие из них содержат (в явном или неявном виде) квантор и как следует устанавливать их значение истинности (указать только способ и обосновать его выбор): а) От перестановки слагаемых сумма не изменяется; б) Два соседних слагаемых можно заменять их суммой; в) Площадь прямоугольника равна произведению его длины на ширину; г) Существуют четные числа; д) Некоторые числа делятся на 4; е) Среди многоугольников есть треугольники.

9. Сформулируйте отрицания следующих предложений: а) Число 123 делится на 9; б) При делении числа 32 на 5 в остатке получится 7; в) 3+2

11. Определите, являются данные предложения отрицаниями друг друга, или нет; объясните – почему: а) Число 12 – четное. Число 12 – нечетное; б) Все простые числа нечетны. Все простые числа четны; в) Все простые числа нечетны. Существуют четные простые числа; г) Некоторые углы острые. Некоторые углы тупые.

12. Переформулируйте данные предложения так, чтобы они не содержали слов «неверно, что», но имели тот же смысл: а) Неверно, что число 9 – четное или простое; б) Неверно, что треугольник АВС – равнобедренный и прямоугольный; в) Неверно, что каждый четырехугольник является прямоугольником; г) Неверно, что хотя бы в одном прямоугольнике диагонали взаимно перпендикулярны.

13. Сформулируйте предложения, которые начинаются словами «неверно, что» и имеют тот же смысл, что и данные: а) Прямые АВ и СД не параллельны и не пересекаются; б) Стороны четырехугольника АВСД не параллельны или не равны; в) Существуют уравнения, не имеющие действительных корней; г) Все прямоугольники не имеют равных смежных сторон.

14. Постройте отрицания следующих высказываний и выясните, что истинно – данное высказывание или его отрицание: а) Произведение чисел 4070 и 8 меньше, чем сумма чисел 18396 и 14174; б) Частное чисел 25842 и 6 меньше разности чисел 14150 и 9833; в) Среди различных прямоугольников есть такие, площади которых равны; г) Среди чисел есть такие, которые делятся на 5 и на 7; д) Существуют числовые выражения, значения которых нельзя найти.

1. Какие из нижеприведенных предложений являются отрицанием высказывания «Все натуральные числа кратны 5»; свой выбор обоснуйте: а) Все натуральные числа не кратны 5; б) Существуют натуральные числа, не кратные 5; в) Существуют натуральные числа, кратные 5; г) Неверно, что все натуральные числа кратны 5; д) Не все натуральные числа кратны 5.

2. Постройте двумя способами отрицание высказывания: а) Всякое свойство квадрата присуще прямоугольнику; б) Некоторые простые числа являются четными.

3. Известно, что объект Х обладает свойствами a, b, d. Что означает отрицание этого высказывания?

4. Постройте отрицания следующих высказываний: а) существует натуральное число, не делящиеся на 2; б) для любого натурального числа а найдется такое натуральное число, на которое не делится а; в) для любых двух натуральных чисел а, в справедливо одно и только одно из отношений а >в, в > а; г) существуют две непараллельные прямые; д) у всех прямоугольников все углы прямые; е) ни для какого натурального числа а не найдется натуральное число в такое, что а + в

Видео:2.4 Разность множеств, законы де Моргана | Константин Правдин | ИТМОСкачать

Постройте отрицание следующих высказываний, пользуясь законами де Моргана 1) 11 четное или не меньше 4 2) АВСД это Прямоугольник и АВ неравно ВС?

Информатика | 10 — 11 классы

Постройте отрицание следующих высказываний, пользуясь законами де Моргана 1) 11 четное или не меньше 4 2) АВСД это Прямоугольник и АВ неравно ВС.

1)11 нечетное и меньше 4

2) АВСД не Прямоугольник или АВ равно ВС.

Видео:Законы алгебры логики / Закон де Моргана + доказательство [Алгебра логики] #5Скачать

Выполните отрицание следующих высказываний : Все люди — братья?

Выполните отрицание следующих высказываний : Все люди — братья.

У кроликов есть уши.

Некоторые люди — злые.

Пробовал доказать, но учитель говорит что не правильно.

Видео:Правила Де Моргана. Доказательство. Теория множеств.Скачать

Если высказывание содержит одно из этих слов, то какое слово будет у его отрицания?

Если высказывание содержит одно из этих слов, то какое слово будет у его отрицания?

ВСЕГДА НЕКОТОРЫЕ НИКОГДА ВСЕ ИНОГДА.

Видео:Конъюнкция, дизъюнкция, импликация, эквиваленция, отрицание. На примерах из жизни. Логика.Скачать

Постройте таблицу истинности для сложного высказывания _ _ (А + В) * С?

Постройте таблицу истинности для сложного высказывания _ _ (А + В) * С.

Видео:3.8 Де Морган правилаСкачать

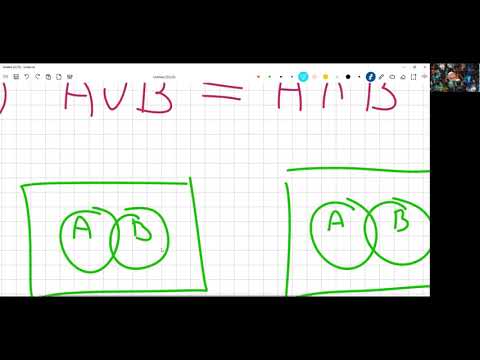
Постройте отрицания следующих высказываний неверно, что число 3 не является делителем числа 198?

Постройте отрицания следующих высказываний неверно, что число 3 не является делителем числа 198.

Видео:Законы де Моргана. ЛогикаСкачать

Логическая операция, имеющая значение «истина», если исходное высказывание ложно, а «ложь» – если исходное высказывание истинно?

Логическая операция, имеющая значение «истина», если исходное высказывание ложно, а «ложь» – если исходное высказывание истинно?

А)отрицание Б)дизъюнкция В)конъюнкция Г)композиция.

Видео:Логика и множества. Утверждения и отрицанияСкачать

Для какого из приведенных чисел истинно высказывание НЕ(число четное) И (число больше 25)?

Для какого из приведенных чисел истинно высказывание НЕ(число четное) И (число больше 25).

Видео:Как устроено отрицание кванторов? Душкин объяснитСкачать

Дано высказывание «Винни — Пух любит мед, и дверь в дом открыта»?

Дано высказывание «Винни — Пух любит мед, и дверь в дом открыта».

Сформулируйте отрицание этого высказывания с точки зрения формальной логики.

Видео:Закон поглощения + доказательство. Преобразование логических выражений [Алгебра логики] #7Скачать

Даны два высказывания : А — «В Африке водятся жирафы» и В — «В Мурманске идет снег»?

Даны два высказывания : А — «В Африке водятся жирафы» и В — «В Мурманске идет снег».

Постройте из них три различных сложных высказывания.

Видео:Введение в логику, урок 4: Предикаты и кванторыСкачать

Для какого из приведенных чисел ложное высказывание : НЕ (число четное) Или ( число?

Для какого из приведенных чисел ложное высказывание : НЕ (число четное) Или ( число.

Видео:Операции над множествамиСкачать

Постройте таблицу истинности высказывания(с&a) эквивалентно b?

Постройте таблицу истинности высказывания

(с&a) эквивалентно b.

На странице вопроса Постройте отрицание следующих высказываний, пользуясь законами де Моргана 1) 11 четное или не меньше 4 2) АВСД это Прямоугольник и АВ неравно ВС? из категории Информатика вы найдете ответ для уровня учащихся 10 — 11 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

🔍 Видео

Отрицание высказываний и высказывательных форм. (пункт 21. по учебнику Стойловой Л.П. Математика)Скачать

Лекция 67. Теорема де МорганаСкачать

Отрицание, Дизъюнкция и Конъюнкция. Графическое решение логических выражений. Алгебра логики основыСкачать

Множества. Доказательство равенстваСкачать

Закон отрицания отрицания, 1982Скачать

Предикаты и кванторы. Отрицание предложений с кванторами.Скачать

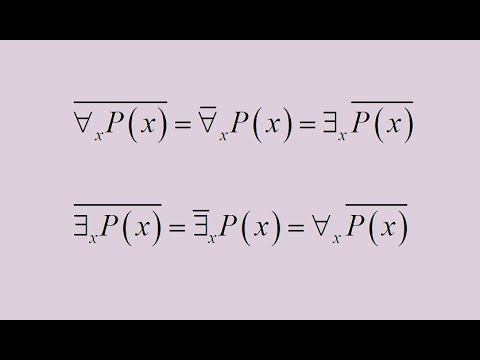
Кванторы Определение и видыСкачать

ИНФОРМАТИКА 8 класс: Высказывание. Логические операции.Скачать