Остроугольный треугольник изображен на рисунке (4 видео)

Треугольник. Медиана, биссектриса, высота, средняя линия.

Содержание

теория по математике 📈 планиметрия
Виды треугольников по углам
Виды треугольников по сторонам
Медиана, биссектриса, высота, средняя линия треугольника
Медиана
Биссектриса
Высота
Средняя линия
Мерзляк 5 класс — § 14. Треугольник и его виды
Вопросы к параграфу
Решаем устно
Упражнения
Упражнения для повторения
Задача от мудрой совы
Виды треугольников (по сторонам)
🔍 Видео

теория по математике 📈 планиметрия

Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.

Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.

Виды треугольников по углам

Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.

Остроугольные	Тупоугольные	Прямоугольные
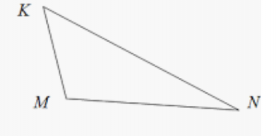
Остроугольным треугольником называется треугольник, у которого все три угла острые. На рисунке показан такой остроугольный треугольник АВС.	Тупоугольным называется треугольник, у которого есть тупой угол. В треугольнике может быть только один тупой угол. На рисунке показан треугольник такого вида, где угол М – тупой.	Прямоугольным называется треугольник, у которого есть угол, равный 90 0 (прямой угол). На рисунке угол С равен 90 0 . Такой угол в любом прямоугольном треугольнике – единственный.

Виды треугольников по сторонам

Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.

Разносторонний	Равнобедренный	Равносторонний
Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС.	Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС.	Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС.

Видео:Остроугольный треугольникСкачать

Медиана, биссектриса, высота, средняя линия треугольника

Медиана

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.

По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.

Биссектриса

Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.

В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD₁, EE₁ и CC₁.

По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.

Высота

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.

На рисунке показаны высоты треугольника АВС: АН₁, ВН₂ и СН₃.

По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.

Средняя линия

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.

Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.

Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 90 0 .

Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.

Составим отношение сторон:

A E A B . . = A B A F . . откуда по свойству пропорции АВ 2 =АЕ ∙ АF

Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.

Составим отношение сторон:

A E A D . . = A C A F . . ; откуда выразим AD= A E ∙ A F А C . . = A E ∙ A F A C . .

Теперь рассмотрим наши два полученных равенства: АВ 2 =АЕ ∙ АF и AD= A E ∙ A F A C . .

Видим, что 36 2 =АЕ ∙ АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD= A E ∙ A F A C . . = 36 2 54 . . = 24

Теперь найдем CD=AC-AD=54-24=30

pазбирался: Даниил Романович | обсудить разбор | оценить

На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.

pазбирался: Даниил Романович | обсудить разбор | оценить

В треугольнике АВС известно, что угол ВАС равен 84 0 , АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0

pазбирался: Даниил Романович | обсудить разбор | оценить

Видео:Треугольники: остро-, тупо- и прямоугольныеСкачать

Мерзляк 5 класс — § 14. Треугольник и его виды

Вопросы к параграфу

1. Какие бывают виды треугольников в зависимости от вида их углов?

остроугольные — все из углы острые;
прямоугольные — один из углов треугольника прямой — равен 90°;
тупоугольные — один из углов треугольника тупой.

2. Какой треугольник называют остроугольным? Прямоугольным? Тупоугольным?

Остроугольные прямоугольники — это треугольники, у которых все углы острые (
Прямоугольные треугольники — это прямоугольники, у которых один из углов прямой (= 90°).
Тупоугольные треугольники — это треугольники, у которых один из углов тупой (> 90°).

3. Какие бывают виды треугольников в зависимости от количества равных сторон?

равнобедренные треугольники — 2 стороны равны;
равносторонние треугольники — 3 стороны равны.

4. Какой треугольник называют равнобедренным? Равносторонним? Разносторонним?

Равнобедренный треугольник — это треугольник, у которого две стороны равны.
Равносторонний треугольник — это треугольник, у которого три стороны равны.
Разносторонний треугольник — это треугольник, у которого все стороны имеют различную длину.

5. Как называют стороны равнобедренного треугольника?

равные стороны равнобедренного треугольника называют боковыми сторонами;
отличающуюся по длине сторону равнобедренного треугольника называют основанием.

6. По какой формуле вычисляют периметр равностороннего треугольника? — Периметр равностороннего треугольника равен произведению числа 3 и длины его стороны : P = 3a.

Решаем устно

1. Чему равен периметр восьмиугольника, каждая сторона которого равна 4 см?

8 • 4 = 32 (см) — периметр восьмиугольника.

2. Вычислите сумму 27 + 16 + 33 + 24.

27 + 16 + 33 + 24 = (27 + 33) = (16 + 24) = 60 + 40 = 100

3. Каких чисел не хватает в цепочке вычислений?

4. На трёх кустах расцвело 15 роз. Когда на одном из этих кустов распустились ещё 3 розы, то на всех кустах роз стало поровну. Сколько роз было на каждом кусте вначале?

1) Мы знаем, что вначале на всех кустах было 15 роз, но потом на одной розе распустилось ещё 3 цветка:

15 + 3 = 18 (цветов) — стало на всех кустах в конце.

2) Мы знаем, что в конце на каждом из трёх кустов роз было поровну:

18 : 3 = 6 (цветов) — было на каждом кусте в конце.

3) Мы знаем, что на одном из кустов роз вначале было на 3 меньше:

6 — 3 = 3 (цветка) — было на одном из кустов вначале.

4) Мы знаем, что количество роз на остальных кустах не изменилось, то есть было и осталось по 6 цветков.

Ответ: 6, 6 и 3 розы.

Упражнения

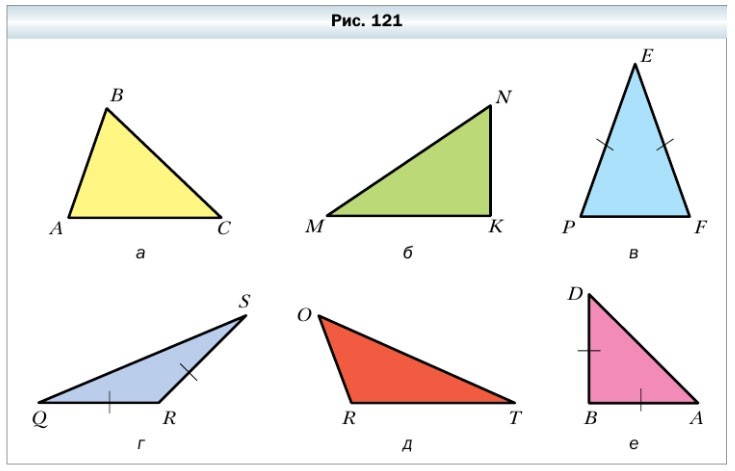
338. Определите вид треугольника, изображённого на рисунке 121, в зависимости от вида его углов и количества равных сторон.

а) треугольник ABC — это разносторонний остроугольный треугольник;
б) треугольник MNK — это разносторонний прямоугольный треугольник;
в) треугольник PEF — это равнобедренный остроугольный треугольник;
г) треугольник QSR — это равнобедренный тупоугольный треугольник;
д) треугольник OTR — это разносторонний тупоугольный треугольник;
е) треугольник DAB — это равнобедренный прямоугольный треугольник.

339. Начертите:

RTQ — разносторонний остроугольный треугольник;
JLD — равнобедренный прямоугольный треугольник;
POS — равнобедренный тупоугольный треугольник.

340. Начертите:

ABC — разносторонний прямоугольный треугольник;
MNK — разносторонний тупоугольный треугольник;
EFH — равнобедренный остроугольный треугольник.

341. Найдите периметр треугольника со сторонами 16 см, 22 см и 28 см.

Периметр треугольника равен сумме длин все его сторон.

P = 16 + 22 + 28 = 66 (см)

342. Найдите периметр треугольника со сторонами 14 см, 17 см и 17 см.

Периметр треугольника равен сумме длин все его сторон.

P = 14 + 17 + 17 = 48 (см)

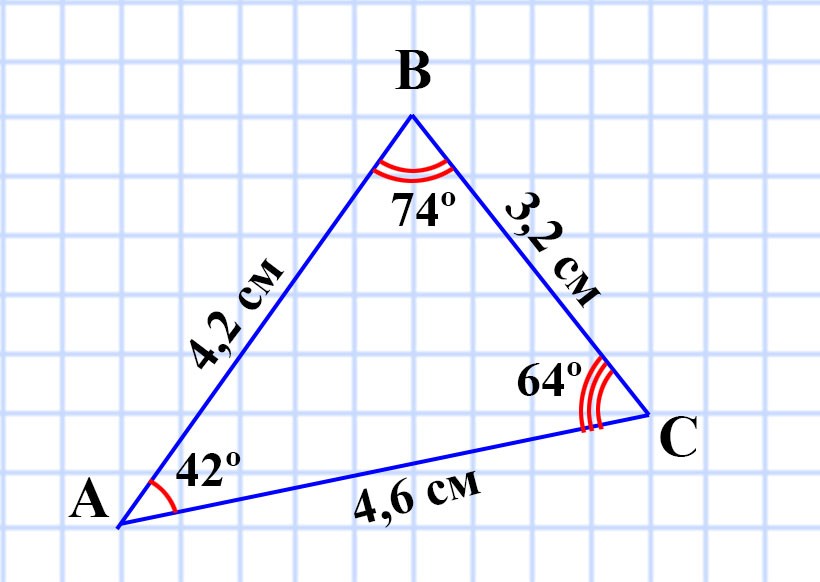
343. Начертите произвольный треугольник, измерьте его стороны и углы, найдите периметр и сумму углов этого треугольника.

Начертим произвольный треугольник ABC.

При помощи линейки измерим длины его сторон:

При помощи транспортира измерим его углы:

Найдём периметр треугольника ABC:

P = AB + BC + AC =4,2 + 3,2 + 4,6 = 12 (см)

∠A + ∠B + ∠C = 42º + 74º + 64º = 180º

Ответ: в треугольнике ABC: AB = 4,2 см, BC = 3,2 см, AC = 4,6 см, ∠A = 42º, ∠B = 74º, ∠C = 64º, периметр P = 12 см, сумма углов равна 180º.

344. Одна сторона треугольника равна 24 см, вторая сторона — на 18 см больше первой, а третья сторона — в 2 раза меньше второй. Найдите периметр треугольника.

1) 24 + 18 = 42 (см) — длина второй стороны треугольника.

2) 42 : 2 = 21 (см) — длина третьей стороны треугольника.

3) 24 + 42 + 21 = 87 (см) — периметр треугольника.

345. Одна сторона треугольника равна 12 см, вторая сторона в 3 раза больше первой, а третья — на 8 см меньше второй. Найдите периметр треугольника.

1) 12 • 3 = 36 (см) — длина второй стороны треугольника.

2) 36 — 8 = 28 (см) — длина третьей стороны треугольника.

3) 12 + 36 + 28 = 78 (см) — периметр треугольника.

346. 1) Найдите периметр равнобедренного треугольника, основание которого равно 13 см, а боковая сторона — 8 см.

У равнобедренного треугольника боковые стороны равны. Значит у данного треугольника дву стороны по 8 см и одна сторона (основание) — 13 см. Найдём периметр:

8 + 8 + 13 = 29 (см) — периметр треугольника.

2) Периметр равнобедренного треугольника равен 39 см, а основание — 15 см. Найдите боковые стороны треугольника.

Мы знаем, тто периметр треугольника — это сумма длин всех его сторон. Также мы знаем, что боковые стороны равнобедренного треугольника равны. Найдем длину боковой стороны:

(39 — 15) : 2 = 24 : 2 = 12 (см) — длина боковой стороны.

Ответ: Каждая из двух боковых сторон этого равнобедренного треугольника равна 12 см.

347. Периметр равнобедренного треугольника равен 28 см, а боковая сторона — 10 см. Найдите основание треугольника.

Мы знаем, тто периметр треугольника — это сумма длин всех его сторон. Также мы знаем, что боковые стороны равнобедренного треугольника равны. Найдем длину основания:

28 — 10 • 2 = 28 — 20 = 8 (см) — длина основания.

348. Периметр треугольника равен p см, одна сторона — 22 см, вторая сторона — b см. Составьте выражение для нахождения третьей стороны. Вычислите длину третьей стороны, если р = 72, b = 26.

Пусть третья сторона равна с см. Составим выражения для нахождения длины третьей стороны треугольника:

При р = 72, b = 26:

с = 72 — 22 — 26 = 50 — 26 = 24 (см).

Ответ: с = p — 22 — b, с = 24 см.

349. Периметр треугольника равен 97 см, одна сторона — а см, вторая — b см. Составьте выражение для нахождения третьей стороны. Вычислите длину третьей стороны, если а = 32, b = 26.

Пусть третья сторона равна с см. Составим выражения для нахождения длины третьей стороны треугольника:

При а = 32, b = 26:

с = 97 — 32 — 26 = 65 — 26 = 39 (см).

Ответ: с = 97 — а — b, с = 39 см.

350. С помощью линейки и транспортира постройте треугольник ABC и укажите его вид, если:

1) две стороны равны 3 см и 6 см, а угол между ними — 40° — разносторонний тупоугольный треугольник (тупым является угол B).

2) две стороны равны 2 см 5 мм и 5 см, а угол между ними — 130° — разносторонний тупоугольный треугольник (тупым является угол А).

3) две стороны равны по 3 см 5 мм, а угол между ними — 54° — равнобедренный остроугольный треугольник

4) сторона АВ равна 4 см, а углы САВ и СВА соответственно равны 30° и 70° — разносторонний остроугольный треугольник.

5) сторона АВ равна 2 см 5 мм, а углы САВ и СВА соответственно равны 100° и 20° — разносторонний тупоугольный треугольник.

6) сторона ВС равна 5 см, а углы ABC и ВСА соответственно равны 30° и 60° — разносторонний прямоугольный треугольник.

7) сторона ВС равна 5 см 5 мм, а углы ABC и ВСА равны по 45° — равнобедренный прямоугольный треугольник.

8) сторона АС равна 5 см 5 мм, а углы ВАС и ВСА равны по 60°

351. С помощью линейки и транспортира постройте треугольник ABC и укажите его вид, если:

1) две стороны равны 3 см и 4 см, а угол между ними — 90° — разносторонний прямоугольный треугольник.

2) две стороны равны по 4 см 5 мм, а угол между ними — 60° — равносторонний остроугольный треугольник.

3) сторона АС равна 6 см, а углы ВАС и ВСА соответственно равны 90° и 45° — равнобедренный прямоугольный треугольник.

4) сторона АВ равна 4 см 5 мм, а углы САВ и СВА соответственно равны 35° — равнобедренный тупоугольный треугольник.

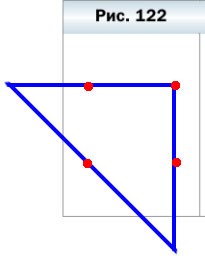
352. Постройте треугольник, стороны которого содержат четыре точки, изображённые на рисунке 122.

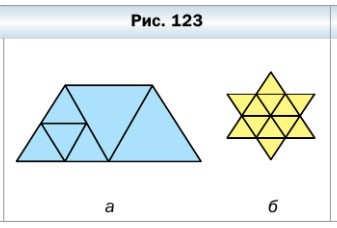
353. Сколько треугольников изображено на рисунке 123?

а) Изображено 7 треугольников (4 маленьких и 3 больших).
б) Изображено 20 треугольников(12 маленьких, 6 средних и 2 больших).

Упражнения для повторения

354. Запишите все углы, изображённые на рисунке 124, и укажите вид каждого угла.

∠ABC — развёрнутый угол
∠ABM — острый угол
∠ABK — тупой угол
∠MBK — прямой угол
∠MBC — тупой угол
∠KBC — острый угол

355. Миша делал домашнее задание по математике с 16 ч 48 мин до 17 ч 16 мин, а Дима — с 17 ч 53 мин до 18 ч 20 мин. Кто из мальчиков дольше делал задание и на сколько минут?

1) 17 ч 16 мин — 16 ч 48 мин = 16 ч 76 мин — 16 ч 48 мин = 28 мин — делал задание Миша.

2) 18 ч 20 мин — 17 ч 53 мин = 17 ч 80 мин — 17 ч 53 мин = 27 мин — делал задание Дима.

3) 28 мин — 27 мин = 1 мин — делал дольше Миша, чем Дима.

Ответ: Миа делал домашнее задание на 1 минуту дольше, чем Дима.

356. Решите уравнение:

357. Вместо звёздочек поставьте цифры так, чтобы действие было выполнено правильно:

Задача от мудрой совы

358. Каждый учащийся гимназии изучает по крайней мере один из двух иностранных языков. Английский язык изучают 328 учеников, французский язык — 246 учеников, а английский и французский одновременно — 109 учеников. Сколько всего учеников учится в гимназии?

1) 328 — 109 = 219 (учеников) — изучает только английский язык.

2) 246 — 109 = 137 (учеников) — изучает только французский язык.

3) 219 + 109 + 137 = 465 (учеников) — всего в гимназии.

Видео:7 класс, 32 урок, Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Виды треугольников (по сторонам)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке учащимся предоставляется возможность обобщить знания о названиях и изученных свойствах геометрических фигур, познакомиться с основными свойствами треугольника, узнать виды треугольников по величине угла, по числу равных сторон, потренироваться в распознавании названных видов.