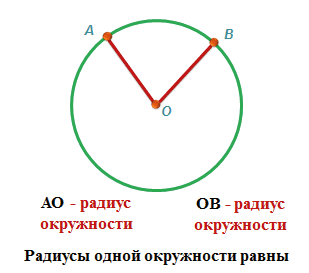
Диаметр окружности для 4 класса (7 видео)

Окружность

Приступаем к изучению окружности и круга. Вспомним замкнутые и незамкнутые линии. Познакомимся с центром окружности, радиусом и диаметром и научимся определять радиус при известном диаметре и диаметр при известном радиусе.

Содержание

Окружность и овал
Правило:
Окружность и круг
Диаметр и радиус
Как найти диаметр окружности
Основные понятия
Как узнать диаметр. Формулы
1. Общая формула.
2. Если перед нами стоит задача найти диаметр по длине окружности
3. Если есть чертеж окружности
Открытый урок по математике в 4 классе по теме «Окружность. Круг. Радиус. Диаметр» УМК «Перспектива» план-конспект урока по математике (4 класс) на тему
Скачать:
Предварительный просмотр:
🎬 Видео

Окружность и овал

Для начала рассмотрим рисунок и найдём окружность:

Теперь рассмотрим сходства и различия этих геометрических фигур:

Центр в точке О

Есть точки A,B,C,D

Овал	Окружность

Сходства
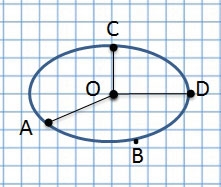
Различия	В овале отрезки от точки O до крайней линии разные, а в окружности – все отрезки одинаковые.

Правило:

Окружность – это замкнутая кривая линия с точкой О в середине, которая называется центром.

Расстояния от центра до линии окружности одинаковые.

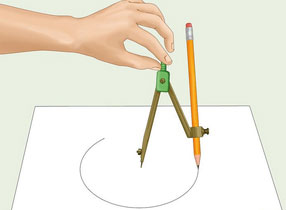
Начертить окружность можно при помощи циркуля:

А овал рисуют от руки:

Окружность и круг

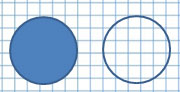
Если заполнить пространство внутри окружности, то получим круг.

Круг – это часть плоскости, ограниченная окружностью.

Диаметр и радиус

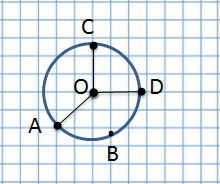
Если соединить центр окружности с линией окружности, получим радиус, например, OC, OA и OD.

Радиус – длина отрезка, соединяющего центр окружности с любой точкой, лежащей на окружности. Радиус составляет половину диаметра.

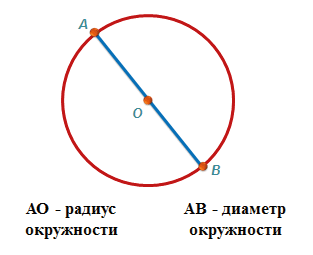
Если отрезок проходит через центр и соединяет две точки на окружности – это диаметр.

Диаметр – это длина отрезка, проходящего через центр окружности и соединяющего две точки на этой окружности.

Поделись с друзьями в социальных сетях:

Видео:Радиус и диаметрСкачать

Как найти диаметр окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Круг. Окружность (центр, радиус, диаметр)Скачать

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.

Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.

Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.

Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.

Радиус — отрезок, который соединяет центр окружности и любую точку на ней.

Видео:РАДИУС ОКРУЖНОСТЬ ДИАМЕТР КРУГ / 3 КЛАСС МАТЕМАТИКА. ЧТО ТАКОЕ ОКРУЖНОСТЬ ? ЧТО ТАКОЕ РАДИУС ?Скачать

Как узнать диаметр. Формулы

В данной теме нам предстоит узнать три формулы:

1. Общая формула.

Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.

2. Если перед нами стоит задача найти диаметр по длине окружности

D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.

Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.

3. Если есть чертеж окружности

Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.

Отметить точки пересечения прямой и окружности.

Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.

Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.

Теперь осталось измерить диаметр круга при помощи линейки. Получилось!

Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.

Видео:Окружность. Как найти Радиус и ДиаметрСкачать

Открытый урок по математике в 4 классе по теме «Окружность. Круг. Радиус. Диаметр» УМК «Перспектива»
план-конспект урока по математике (4 класс) на тему

В данной разработке урока, составленному с соответствии с ФГОС для 4 класса по УМК «Перспектива», представлены конспект урока, презентация, карточки с самостоятельной работой и лист индивидуальной работы учащихся.

Видео:Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

Скачать:

Вложение	Размер
konspekt_uroka.doc	80.5 КБ
okruzhnost_krug.ppt	2.78 МБ
samostoyatelnaya_rabota.docx	250.58 КБ
individualnyy_list.docx	44.37 КБ

Видео:Окружность. Круг. 5 класс.Скачать

Предварительный просмотр:

1) формировать представление об окружности и её элементах: центре, диаметре, радиусе, умение строить окружности с помощью циркуля;

2) тренировать вычислительный навык, умение решать текстовые задачи.

Мыслительные операции, необходимые на этапе проектирования: анализ, сравнение, обобщение.

Мотивация к учебной деятельности.

-Ребята, в начале урока математики я хотела бы прочитать слова удивительного человека, учёного, поэта Михаила Васильевича Ломоносова, который родился в 1711году.

«Математику уже затем учить надо, что она ум в порядок приводит».

Сегодня на уроке мы тоже постараемся упорядочить наши знания.

Посмотрите на этого забавного слоненка. Из какой области математики он к нам пожаловал? (Из геометрии.)
Что в нём необычного? (Он состоит из одних кругов.)
Именно геометрии, именно кругам мы посвятим сегодняшний урок и узнаем что-то новое о них. Как вы будете узнавать новое? (Мы должны постараться сами понять, что мы еще не знаем, а потом постараться самостоятельно «открыть» новое знание.)
Желаю вам успехов в работе.

2. Актуализация знаний и фиксация индивидуального затруднения в пробном действии.

Для начала поделимся со слоненком вашими успехами в изучении приемов умножения и деления.
Найдите и запишите значения выражений на ваших листочках.
Проверим ответы первого варианта.
Проверим ответы второго варианта .
Кто из вас ошибся при выполнении задания?
Сделайте вывод. (Нужно закрепить знание умножения и деления круглых чисел.)
Почему ответы на карточках? (Наверно, в них спрятан какой-то секрет.)
Верно, надо лишь перевернуть карточки.

Прочитайте слова.
Объясните понятия «область» и «граница» с точки зрения геометрии. (Граница – это линия, которая ограничивает фигуру, идёт по её «краю»; область – это часть плоскости, которая находится внутри границы…)

Слоненок хочет приобрести себе домик в стране Геометрии. У него есть на выбор 4 участка. Их планы изображены на этом рисунке.
Посмотрите, что в них интересного? (Это геометрические фигуры).
Назови, что это за фигуры?

Некоторые их точки обозначены буквами. Где располагаются точки? (внутри, на границе) .

Чтобы слоненок приобрёл себе участок с домиком, ему надо составить два слова, которые дают ключ к его участку. Одно слово состоит из букв, стоящих на границах фигур, а другое – из букв, стоящих внутри границ . Поможете ему?
Составьте эти слова. (Круг, окружность.)
Что такое круг и чем он отличается от окружности? (Круг – это часть плоскости внутри окружности, окружность – это граница круга.)
Слоненок вам очень признателен

Посмотрите ещё раз внимательно на него. Найдите в его изображении круги и окружности.

— Чтобы понять , с чем мы познакомимся на уроке поиграем в игру «Верю не верю». В конце урока проверим ваши предположения.

3) Пробное действие.

Что вы повторили и узнали? (Мы повторили способы умножения и деления круглых чисел, что называется границей и областью, узнали, что такое окружность, потренировались в определении кругов и окружностей на рисунке.)
Почему я выбрала именно это? (Это нам пригодится для открытия нового знания.)
Какое следующее задание я вам предложу? (Пробное задание.)
Зачем вы его получите? (Чтобы мы сами узнали, что мы еще не знаем.)
Попробуйте построить окружность и начертите ее радиус.

— Приступайте к выполнению задания.

Итак, посмотрим, что у вас получилось.
Кто не выполнил это задание?
Что вы не смогли сделать? (Мы не смогли построить окружность и начертить радиус.)
Кто выполнил задание?

Значит, что вы не смогли сделать? (Мы не смогли нарисовать окружности правильно и начертить радиус .)
Что же теперь делать? (Нужно разбираться в затруднении.)

3. Выявление места и причины затруднения.

Какое задание вы должны были выполнить? (Мы должны были начертить окружность, радиус.)

В чем затруднение? ( Не знаем, что такое радиус.)

4. Построение проекта выхода из затруднения.

Какую цель вы поставите перед собой на уроке? («Открыть» способ построения окружностей, узнать что такое радиус.)
С помощью чего можно изобразить окружность? (С помощью циркуля)
Выступление ученика
Самый старый железный циркуль обнаружен во Франции при раскопках древнего кургана. Он пролежал в земле более 2-х тысяч лет. В пепле, засыпавшем греческий город Помпеи, археологи обнаружили очень много бронзовых циркулей.
Приготовьте циркуль. Посмотрите на него внимательно (у учителя большой циркуль) .
— Из чего он состоит (2 ножки, на конце первой иголочка, на конце второй – грифель – это карандаш) .
— Циркуль – это чертёжный инструмент для вычеркивания окружностей. В переводе с латинского обозначает круг — циркус. С каким словом созвучно мое название? «Цирк – циркуль «циркулюс» (круг). У цирка арена круглая, что представляется удобным для просмотра выступления артистов цирка.
С циркулем нужно работать очень осторожно.
Назовите правила как пользоваться циркулем .
У каждой фигуры есть свой алгоритм построения. У окружности он тоже имеется.

Прочитайте план.
Он вам понятен?

Что теперь вы должны сделать? (Выполнить данный план.)

5. Реализация построенного проекта.

Какой первый шаг? (Отметить точку О)
Эта замкнутая линия и называется окружность, а О точка ? (центр окружности. )

— Отметьте на окружности две точки и соедините их с центром. (Провели несколько радиусов).

— Одинаковые ли они по длине? (да)

— Сами попробуйте сформулировать определение радиуса (r – это отрезок, соединяет центр окружности с точкой на окружности) .

1)Расстояние от центра окружности до любой точки окружности называется радиусом .

2) Радиусы равны.

Ещё вавилоняне и древние индийцы считали самым важным элементом окружности – радиус. Слово это латинское и означает “луч”. В древности не было этого термина: Евклид и другие учёные говорили просто “прямая из центра”.

Термин “радиус” становится лишь в конце XVII в. Впервые термин “радиус” встречается в “Геометрии” французского ученого Рамса, изданной в 1569 году.

— Приступаем к практической работе.

– Возьмите круг. Сложите пополам. Найдите линию сгиба. Обведите её любым цветным карандашом.

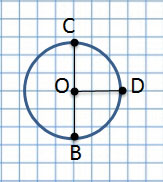
Если соединить линией две противоположные точки окружности, то такая линия будет проходить через центр окружности. Называется такая линия диаметром окружности.

— Начертите диаметр АВ.

— Сами сформулируйте определение диаметра (отрезок, соединяющий две точки окружности, и проходит через центр) .

Сравните длину радиуса и длину диаметра. Какой вывод можно сделать?

Какими фигурами являются радиус и диаметр окружности? (Отрезками.)
Прочтите, что об этом написано в желтой рамке под чертежом.

Итак, что вы узнали об окружности ? (Окружность – это граница круга, радиус соединяет центр окружности с ее точной; если две противоположные точки соединить отрезком, проходящим через центр окружности, то получим диаметр.)

Учитель вывешивает на доску эталон.

Смогли вы преодолеть затруднение? (Да.)

Что теперь вы можете делать? (Строить окружности, радиусы, диаметры.)
Самая простая из кривых линий – окружность. Ведь это одна из древнейших геометрических фигур. В Древней Греции круг и окружность считались венцом совершенства.

Физминутка В жизни мы часто встречаемся с кругом и окружностью.

Сейчас мы поиграем ,посмотрим какие вы внимательные: я вам буду называть предметы, если они имеют форму круга-то вы садитесь, если форму окружности то вы хлопаете Бублик(хлопок), тарелка (приседание),

Баранка, колесо, скатерть круглая, кольцо, обруч, крышка, зеркало.

Молодцы: и отдохнули, и поиграли.

Какой следующий шаг на уроке? (Закрепить новые знания.)

6. Первичное закрепление с проговариванием во внешней речи.

1) Фронтальная работа.

1)- Начертите окружность радиусом 2 см. Отметьте центр окружности и проведите её радиус. Обозначьте точками. Проведите диаметр этой окружности, измерьте его длину. Во сколько раз диаметр окружности больше ее радиуса ?

2) Работа в парах.

2) Не нарушая закономерностей, построй радиусы в последних окружностях.
Выберите на рисунке на доске те окружности, в которых проведен диаметр.

Учащиеся выполняют задание в парах с комментированием. Проверка организуется по образцу.

Проверьте свои результаты.
Кто из вас ошибся?
Какой следующий шаг на уроке? (Проверить себя, справимся ли мы самостоятельно.)

7. Самоконтроль с самопроверкой по эталону.

— Возьмите из конверта листы с самостоятельной работой.

Учащиеся выполняют самостоятельную работу.

Проверка организуется по образцу. Учитель вывешивает образец рядом с эталоном Д-9.

Кто из вас ошибся?
В каком случае? Исправьте ошибку.
Сделайте вывод. (Нужно еще потренироваться.)
Кто не ошибся?
Сделайте вывод. (Мы все хорошо усвоили .)

8. Включение в систему знаний и повторение.

Где вам может пригодиться умение чертить окружности? (На уроках труда, при дальнейшем изучении математики, …)
В конце урока я предлагаю потренироваться.

Учебник стр. 51, №8
Кто из вас ошибся?
В чем ошибка?
Где вы можете поработать над ошибками? (Дома.)

Игра «Будь внимательным!» .

Сколько окружностей нужно начертить, чтобы получился такой рисунок?

— Окружность — волшебная геометрическая фигура. С ее помощью можно совершить чудесные превращения…

9. Рефлексия учебной деятельности на уроке.

Какую цель урока вы ставили перед собой? («Открыть» способ построения окружности, узнать что такое радиус.)

Достигли ли вы цели? Докажите. (Окружность это граница круга, радиус – это отрезок…)
Что еще узнали на уроке? Выберите предложение и расскажите. (….)
Кто вам помог открыть способ? (Слоненок.)

Теперь я предлагаю вам оценить свою работу на уроке. На плакате нарисован цирковой слон. Он очень любит жонглировать мячами, но сегодня мячей у него нет. У вас на столе есть цветные круги. Выберите круг так:

красный круг, если вы выполнили задания, самостоятельную работу без ошибок, и у вас нет вопросов;
фиолетовый круг – если вы выполнили задания, самостоятельную работу, но у вас остались вопросы;
белый круг – если вы ошиблись в самостоятельной работе, у вас остались вопросы.

Учащиеся оценивают себя с помощью кругов.

Далее идет обсуждение домашнего задания.

— Спасибо за урок. Мне очень понравилось, как вы работали.