Решение задач на построение сечений
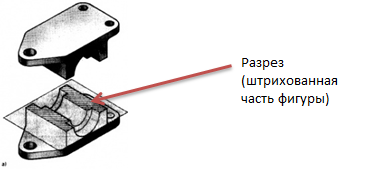
| Подумайте, какой школьный предмет позволяют научиться правильно выполнять и оформлять чертежи, познакомится с различными графическими способами передачи сведений об объектах предметного мира. Правильно! Это черчение. Для изготовления деталей на заводе используются точные чертежи этих деталей в разрезе. Разрезы используются для показа внутренней формы изделия. Разрезом называется изображение, полученное при мысленном рассечении детали одной или несколькими секущими плоскостями. В разрезах показывается то, что получается в секущей плоскости. | На экране изображение  На экране изображение На экране изображение  На экране рисунок На экране рисунок
| ||||||||||||
| При решении геометрических задач связанных с тетраэдром и параллелепипедом тоже иногда необходимо построить разрез фигуры. Только полученное изображение в геометрии называется сечением. Давайте разберёмся, что называется сечением тетраэдра и параллелепипеда. | |||||||||||||
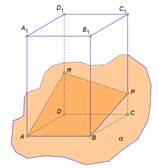
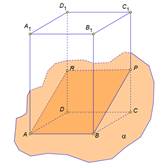
| Секущая плоскость α пересекает грани тетраэдра по отрезкам АЕ, ЕС, АС. Треугольник АЕС, сторонами которого являются эти отрезки, называется сечением тетраэдра. Тетраэдр имеет четыре грани, значит его сечениями могут быть только треугольники и четырехугольник. При пересечении параллелепипеда секущая плоскость также оставляет следы на его боковых гранях в виде отрезков. Отрезки образуют многоугольник, который называется сечением параллелепипеда. Так как у параллелепипеда шесть граней, то в сечении может получиться фигура треугольник, на рисунке вы это видите. Четырехугольник Пятиугольник и шестиугольник . При построении сечений очень легко нарушить геометрические факты, теоремы. Например, данное сечение параллелепипеда плоскостью содержит ошибку. Если плоскость пересекает две параллельные плоскости, то линии их пересечения параллельны. Значит, отрезок АВ и отрезок RP на чертеже должны быть изображены параллельно. А мы наблюдаем, что это не так . Но и отрезки AR и BP тоже не параллельны, хотя лежат в параллельных плоскостях. Значит плоскость α, должна пересекать грани АА1D1D и BB1C1C по параллельным прямым. Исправим ошибки. Или на данном чертеже прямая LM пересекает ребро ВC в точке N. Но это невозможно. Прямая LM принадлежит плоскости АА1D1D, а прямая ВС не лежит в данной плоскости, значит они не могут пересекаться, они скрещивающиеся прямые. Так прямая LM не может пересекать DC, ВВ1 , а вот c прямой AD они пересекаются. Исправим ошибку на чертеже. | На экране текст и изображение: Сечение тетраэдра 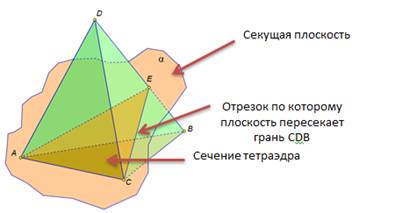 На экране изображение и текст: Виды сечений тетраэдра На экране изображение и текст: Виды сечений тетраэдра
На экране изображение и текст: Сечение параллелепипеда На экране изображение и текст: Виды сечений параллелепипеда
На экране изображение: На экране обновляется изображение На экране обновляется чертёж | ||||||||||||
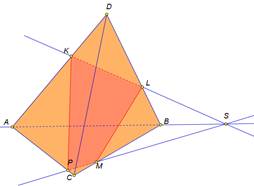
| Рассмотрим примеры построения различных сечений. Дан тетраэдр АВСD . На его рёбрах отмечены точки K,L,M. Построить сечение тетраэдра плоскостью, проходящей через точки K,L,M. Изобразим тетраэдр и данные точки. При построении сечений нужно помнить один факт, что если две плоскости имеют общие точки, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. Так у нас секущая плоскость проходит чрез точки M,L, а они лежат в плоскости CDB, значит ML-линия пересечения плоскостей. Аналогично прямая KL является линией пересечения секущей плоскости и грани ADB Для того чтобы построить линию пересечения с гранью АВС нужны две точки. Точка М уже у нас есть. Для построения второй точки. Продлим до пересечения прямые KL и АВ. Отметим их общую точку S. Точка S принадлежит секущей плоскости, так как ей принадлежит прямая KL и принадлежит грани АВС, так как ей принадлежит прямая АВ. Значит секущая плоскость пересекает плоскость АВС по прямой MS. Построим эту прямую. Отметим точку P- точку пересечения прямой с ребром АС. Отрезок PM- след от сечения грани плоскостью α. Мы получили в результате две точки K и Р В грани АDC. Отрезок КР есть линия пересечения секущей плоскости и грани. Проведем этот отрезок. Четырехугольник KLMP-искомое сечение. | На экране текст. Дан тетраэдр АВСD . На его рёбрах отмечены точки K,L,M. Построить сечение тетраэдра плоскостью, проходящей через точки K,L,M. На экране изображение. 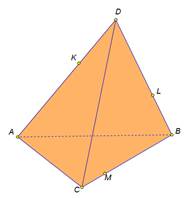 На экране изображение. На экране изображение. 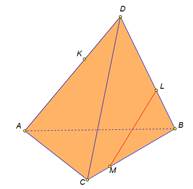 На экране изображение. На экране изображение. 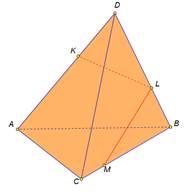 На экране изображение. На экране изображение. 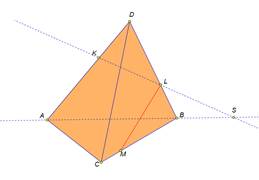 На экране изображение. На экране изображение. 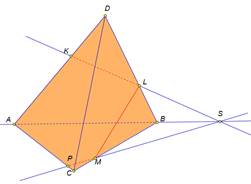 На экране изображение. На экране изображение. 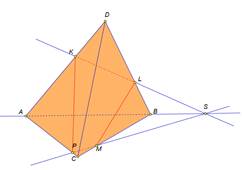 На экране изображение На экране изображение
| ||||||||||||
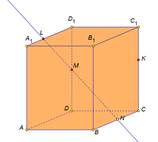
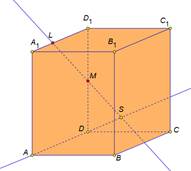
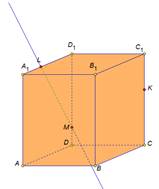
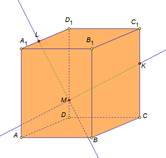
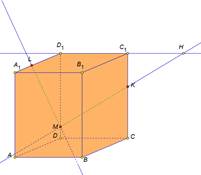
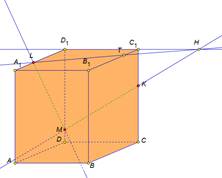
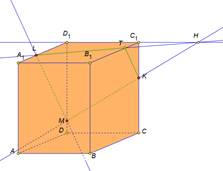
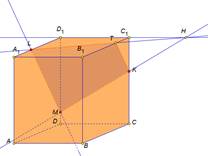
| Рассмотрим задачу на построение сечения параллелепипеда. На рёбрах параллелепипеда даны точки K,L,M. Построить сечение параллелепипеда плоскостью KLM. Построим данный параллелепипед и отметим указанные точки. Так как точки L и M принадлежат грани АА1D1D и секущей плоскости, значит прямая LM их линия пересечения, а отрезок LM след от сечения грани АА1D1D секущей плоскостью. Аналогично в грани DD1C1C построим прямую MK и выделим отрезок MK. В грани А1B1C1D1 есть только одна точка L, для построения второй точки продлим до пересечения прямые D1C1 и MK. Отметим их общую точку H. Точка H принадлежит секущей плоскости, так принадлежит прямой MK. И принадлежит грани A1B1C1D1, так как принадлежит прямой D1C1. Проведем прямую LH. Отметим точку T точку пересечения прямой с ребром B1C1. Выделим отрезок LT это будет след от сечения плоскость. Так как точки T и К принадлежат секущей плоскости и грани ВВ1С1С, то отрезок ТК будет следом от сечения в этой грани. Выделим получившийся четырехугольник KMLT. Это искомое сечение. Рассмотренные задачи относятся к классу задач на построение и имеют свои этапы решения: анализ, построение, доказательство. Мы рассмотрели только этап построения, так как наша цель– научиться строить искомое сечение. | На экране текст: На рёбрах CC1,A1D1, DD1 параллелепипеда АВСDA1B1C1D1 отмечены точки K,L,M соответственно. Построить сечение параллелепипеда плоскостью KLM. На экране изображение: 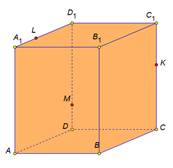 На экране изображение: На экране изображение:
На экране изображение и и текст:
На экране изображение и текст:
На экране изображение и текст:
На экране изображение:
На экране изображение:
Комментарий: задачи разобраны очень подробно, оформлены, четко структурированы. были небольшие опечатки по ходу решения. Содержание
Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать  Задачи на построение сечений в параллелепипедеЭтот видеоурок доступен по абонементуУ вас уже есть абонемент? Войти В ходе урока все желающие смогут получить представление о теме « Задачи на построение сечений в параллелепипеде». Вначале мы повторим четыре основные опорные свойства параллелепипеда. Затем, используя их, решим некоторые типовые задачи на построение сечений в параллелепипеде и на определение площади сечения параллелепипеда. Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать  Сечения параллелепипеда различными плоскостями могут быть : а) шестиугольниками б)пятиугольниками в) треугольниками г) четырехугольниками 1)а, в, г 2)в, г 3)б, в, г 4)а, б, в, г?Геометрия | 10 — 11 классы Сечения параллелепипеда различными плоскостями могут быть : а) шестиугольниками б)пятиугольниками в) треугольниками г) четырехугольниками 1)а, в, г 2)в, г 3)б, в, г 4)а, б, в, г. 3 выриант если что обращайтесь. Видео:Как строить сечения параллелепипедаСкачать  Постройте сечение данного параллелепипеда плоскостью abc?Постройте сечение данного параллелепипеда плоскостью abc. Видео:Как строить сеченияСкачать  Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки P, F и М — середины ребер AA1, A1B1 и DC?Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки P, F и М — середины ребер AA1, A1B1 и DC. Видео:Как строить сечение куба? Стереометрия. 10-11 класс | Математика | TutorOnlineСкачать  Дан параллелепипед АВСДА1В1С1Д1?Дан параллелепипед АВСДА1В1С1Д1. Точка Р лежит в плоскости грани ВСС1 В1 и не принадлежит ребру ВС. Постойте сечение паралепипеда плоскостью проходящей через точку Р параллельно плоскости С1СД. Видео:СЕЧЕНИЯ ТЕТРАЭДРА И ПАРАЛЛЕЛЕПИПЕДАСкачать  Постройте сечение данного параллелепипеда плоскостью ABC?Постройте сечение данного параллелепипеда плоскостью ABC. Видео:Построение сечения параллелепипеда через три точкиСкачать  Построить сечение параллелепипеда?Построить сечение параллелепипеда. Видео:ВСЕ О СЕЧЕНИЯХ В СТЕРЕОМЕТРИИСкачать  СРОЧНО?Постройте сечение параллелепипеда плоскостью, проходящей через точки E и F и параллельной прямой a. Видео:ЕГЭ Математика 13 Задание Сечения прямоугольного параллелепипеда Метод следовСкачать  АВСДА1В1С1Д1 — прямоугольный параллелепипед, СС1 = 9 ?АВСДА1В1С1Д1 — прямоугольный параллелепипед, СС1 = 9 . Точка К лежит на СС1 , причем СК : КС1 = 1 : 2. Периметр сечения параллелепипеда плоскостью АДК = 22. Найдите боковую площадь параллелепипеда. Видео:ПАРАЛЛЕЛЕПИПЕД 10 11 класс сечение параллелепипедаСкачать  Постройте сечение данного параллелепипеда плоскостью MNK?Постройте сечение данного параллелепипеда плоскостью MNK. Видео:Как строить сечения тетраэдра и пирамидыСкачать  50 баллов за решение геометрии с фоткой сечений?50 баллов за решение геометрии с фоткой сечений! С подробным объяснением или хотя бы как провести сечения и двугранные углы! В правильной 4 — угольной призме авсда1в1с1д1 со стороной основания 4 и высотой 7 на ребре АА1 взята точка М, АМ = 2. На ребре ВВ1 точка К, В1К = 2. Построить сечение плоскостью Д1МК, найти угол между этой плоскостью и плоскостью СС1Д1. Через прямую ВД1 проведена плоскость а, параллельная АС. Сечение параллелепипеда плоскостью а — ромб. Докажите, что АВСД — квадрат Найти угол между плоскостью а и плоскостью ВСС1, если АА1 : АВ = 3 : 2. Видео:Геометрия 10 класс (Урок№7 - Тетраэдр и параллелепипед.)Скачать  Через середины M и N ребер AD и CC1 параллелепипедаABCDA1 B1 C1 D1 проведена плоскость параллельно диагонали DB1 ?Через середины M и N ребер AD и CC1 параллелепипеда ABCDA1 B1 C1 D1 проведена плоскость параллельно диагонали DB1 . Постройте сечение параллелепипеда этой плоскостью. В каком отношении она делит ребро BB1 ? Вы перешли к вопросу Сечения параллелепипеда различными плоскостями могут быть : а) шестиугольниками б)пятиугольниками в) треугольниками г) четырехугольниками 1)а, в, г 2)в, г 3)б, в, г 4)а, б, в, г?. Он относится к категории Геометрия, для 10 — 11 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей. Дано ABCD — четырёхугольник Окр (O ; R) вписана : ab + cd = 15 дм P = ? Решение Т. К. ABCD описанный четырехугольник следовательно. Ab + cd = ad + bc т. Е. ad + dc = 15см 2)p = ab + cd + bc + ad = 30 дм. Можно решить и другим способом : sinА = R / 2R = 12 ⇒∠А = 30°. В результате вращения образуется фигура — цилиндр с радиусом 6 см и высотой 6 см V = πR² * H = π6² * 6 = 216π см³ Sп = 2πR * H + 2πR² = π(2 * 6 * 6 + 2 * 6²) = 144π см². Уже сам разберись в записях. 2 * (х + х + 3) = 48 2х + 3 = 48÷ 2 2х + 3 = 24 2х = 24 — 3 2х = 21 х = 10, 5 см 10, 5 + 3 = 13, 5 см. 5) все углы по 60 градусов, т. К. треугольник равносторонний 9) т. К. внешний угол угла М = 130, то угол М = 50 градусов. А т. к. Треугольник равнобедренный, то угол К = 50, а угол N = 80 6) т. К. угол Е = 90, а угол К = 60, то угол Р = 30 7) тр.. BK — высота, медиана, биссектриса ▲АВK. 1) если высоты провести из вершины острого угла, то несложно доказать, что угол между высотами будет равен тупому углу параллелограмма. К этому условию задачи этот вариант не подходит)) 2) если высоты провести из вершины тупого угла, то несложно док.. Из того, что АС = AD ; AE = AB ; и угол А — общий уже следует равенство треугольников АСЕ и ADB (по двум сторонам и углу между ними) (и в этом случае не важно чему именно равен угол А))) из равенства треугольников последует равенство всех остальных с.. Один угол х, второй 2х. Так как треуг. Прямоугольный, то сумма двух этих углов 90 градусов х + 2х = 90 3х = 90 х = 30 2х = 60 градусов — больший угол. 🔍 ВидеоПостроение сечений Занятие 1Скачать  Сечения многогранников. Метод следов.Скачать 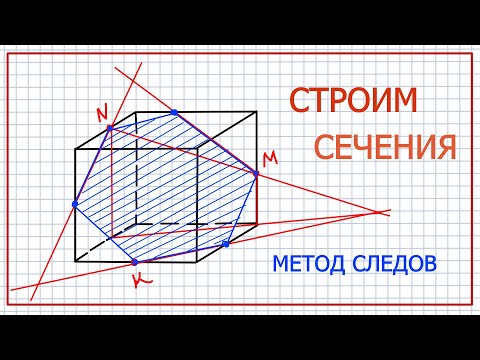 Сечение параллелепипедаСкачать  КАК ПОСТРОИТЬ СЕЧЕНИЕ ТЕТРАЭДРА? #математика #егэматематика #математикапрофильСкачать 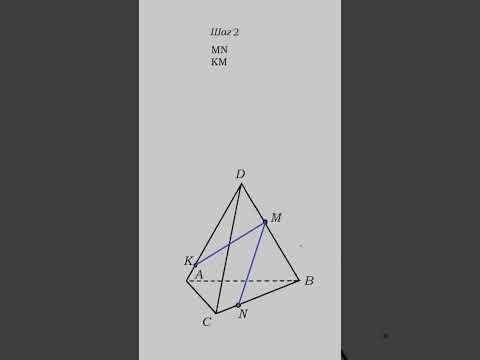 ЕГЭ Задание 14 Параллелепипед СечениеСкачать  №14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать  Построение сечений параллелепипеда, геометрия, 10 класс.Скачать  Построение сечений Занятие 2Скачать  |

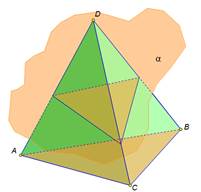 В сечении тераэдра плоскостью лежит треугольник
В сечении тераэдра плоскостью лежит треугольник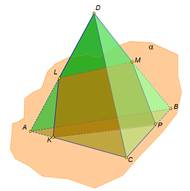 В сечении тетраэдра плоскостью лежит четырёхугольник
В сечении тетраэдра плоскостью лежит четырёхугольник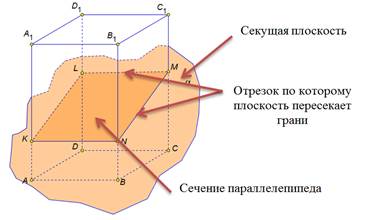
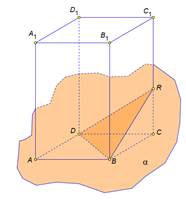 В сечении паралелепипеда плоскостью лежит треугольник
В сечении паралелепипеда плоскостью лежит треугольник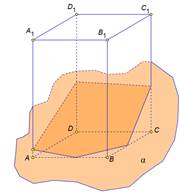 В сечении паралелепипеда плоскостью лежит пятьугольник
В сечении паралелепипеда плоскостью лежит пятьугольник