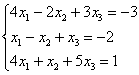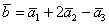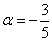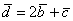В данной публикации мы рассмотрим, каким образом можно разложить вектор по двум базисным векторам, а также разберем пример решения задачи по этой теме.
- Принцип разложения вектора
- Пример задачи
- Разложить вектор по базису матлаб
- Создание Script MFiles
- Алгебраические свойства скалярного произведения:
- Пример 1. Вычисление скалярного произведения в декартовом базисе.
- Пример 2. Вычисление скалярного произведения в косоугольном базисе, состоящем из единичных векторов.
- Пример 3. Вычисление скалярного произведения в косоугольном базисе, состоящем из векторов произвольной длины.
- Определение скалярного произведения через понятие проекции.
- Список вопросов для студентов по КМ 1
- Часть 1. Работа с системой MATLAB
- Часть 2. Теоретическая основа. Контрольные вопросы
- (здесь есть вопросы, которые в практикуме не рассматривались, но знать надо)
- Индивидуальные задания № 1 Векторная алгебра.
- Доказать, что 3 вектора образуют базис трёхмерного пространства и найти координаты 4-го вектора в данном базисе
- 📹 Видео
Видео:Как разложить вектор по базису - bezbotvyСкачать

Принцип разложения вектора
Для того, чтобы разложить вектор b по базисным векторам , требуется определить такие коэффициенты , при которых линейная комбинация векторов равняется вектору b , то есть:
Видео:Найдите разложение вектора по векторам (базису)Скачать

Пример задачи
Разложим вектор по двум базисным векторам и .
Решение:
1. Векторное уравнение выглядит так:
3. Теперь нужно решить систему. Из второго уравнения получаем:
.
Подставляем полученное выражение в первое уравнение:
2 · (1 + 3y) + y = 16
2 + 6y + y = 16
7y = 14
y = 2
Следовательно, x = 1 + 3y = 1 + 2 · 2 = 7 .
Видео:Разложение вектора по базису. 9 класс.Скачать

Разложить вектор по базису матлаб
Название работы: Практикум по линейной алгебре и аналитической геометрии в среде MATLAB
Предметная область: Информатика, кибернетика и программирование
Описание: Цели работы. Работа с графикой: построение векторов на плоскости и в пространстве. Работа с М-файлами. Приобретение навыков решения задач векторной алгебры с помощью средств системы MATLAB. Освоение с помощью графических иллюстраций MATLAB фундаментальных понятий векторной алгебры.
Дата добавления: 2014-09-24
Размер файла: 1.12 MB
Работу скачали: 122 чел.
Практикум по линейной алгебре и аналитической геометрии в среде МАТЛАБ.
Модуль 1. Аналитическая геометрия.
Цель модуля. С помощью графических иллюстраций MATLAB освоить фундаментальные понятия векторной алгебры и аналитической геометрии.
Лабораторный практикум 1.2. Векторная алгебра.
Цели работы. Работа с графикой: построение векторов на плоскости и в пространстве. Работа с М-файлами. Приобретение навыков решения задач векторной алгебры с помощью средств системы MATLAB. Освоение с помощью графических иллюстраций MATLAB фундаментальных понятий векторной алгебры:
геометрический вектор, линейные операции над векторами,
длина вектора, орт вектора, направляющие косинусы,
линейная зависимость двух, трех, четырех и более векторов,
понятие базиса, проекция векторов на ось,
прямоугольная и косоугольная системы координат,
скалярное произведение векторов.
Продолжительность работы. 4 академических часа в аудитории и 4 часа на самостоятельную работу (2 недели)
Срок сдачи : 4,5 недели.
Оборудование, приборы, инструментарий. Письменная часть работы выполняется в тетради, электронная часть работы выполняется в компьютерном классе с использованием пакета MATLAB.
- Упражнения выполняются параллельно с изучением теоретического материала из параллельного курса «Линейная алгебра и аналитическая геометрия», см. приложения, лекции и другую литературу.
- Большинство упражнений необходимо предварительно решать в тетради.
- При выполнении упражнений в случае появления сообщения об ошибке рекомендуется сначала самостоятельно выяснить, чем оно вызвано, и исправить команду; если многократные попытки устранить ошибку не привели к успеху, — проконсультироваться с преподавателем.
- Дома доделать примеры и упражнения, которые Вы не успели выполнить во время занятия; выполнить дополнительные упражнения для самостоятельной работы и ответить на контрольные вопросы.
- Подготовить отчёт, в который включить результаты по упражнениям и развернутые ответы на контрольные вопросы. Отчёт представить
в виде документа Microsoft Word, имя файла (пример): «мп_17_Иванов_Павел_лаб_1_1» (факультет_группа_Фамилия студента_Имя студента_номер лабораторной). По каждому выполненному упражнению отчет должен содержать: - № упражнения; текст упражнения;
- команды, скопированные из командного окна, с комментариями к ним
- результаты их выполнения, включая построенные графики;
- выводы и комментарии к полученным результатам.
*Без предъявления письменных решений электронный отчет не рассматривается. **При проверке решений и отчета у преподавателя не должно возникать необходимости обращаться к источнику задания.
- Геометрические векторы и линейные операции над ними.
Геометрическим вектором (или просто вектором) называется отрезок, концы которого рассматриваются в определенном порядке (т. е. указано, какая из его граничных точек является началом, а какая — концом).
Векторы обозначают символом , либо одной малой полужирной латинской буквой, например, , Если за начало отрезка принята точка , то точку называют точкой приложения вектора.
На чертеже (рис. 1.) вектор изображен отрезком со стрелкой в конечной точке B .
Длиной вектора назовем длину отрезка и в записи используем знак абсолютной величины: (либо ).
Вектор называется нулевым вектором, если его конечная точка совпадает с начальной .
Нулевой вектор, в силу его определения, не имеет направления, а длина его равна нулю.
Векторы и назовем коллинеарными , если они лежат либо на одной прямой, либо на параллельных прямых (рис. 2).
Два вектора и называют равными , если они коллинеарны, имеют общее направление и равные длины (рис. 3).
Из определения следует, что два вектора, равные третьему, равны между собой (Рис. 3.) Именно поэтому в аналитической геометрии не различают равные векторы, имеющие разные точки приложения. Векторы, изучаемые в аналитической геометрии, называются свободными . Обычно их и обозначают малой полужирной латинской буквой, например . Векторы, приложенные к какой-то точке или , называются закрепленными.
Напомним, что сумма двух векторов может быть найдена:
а) по правилу треугольника; б) по правилу параллелограмма (см. рис. 4).
Если векторы и коллинеарны, то “работает” только первое правило.
Кроме того, для любых точек M , N , P плоскости или пространства имеет место правило трёх точек: (см. рис. 5).
Свойства операции сложения геометрических векторов:
1) для любых двух геометрических векторов и :
— переместительное или коммутативное свойство;
2) для любых трёх геометрических векторов , и :
— сочетательное или ассоциативное свойство
(коммутативность от латинского commutativus — «меняющийся»)
(ассоциативность от латинского associatio — соединение).
- Построение векторов в графическом окне MATLAB .
- Построение прямых. Команда line .
С самого начала мы будем использовать визуализацию: изображать векторы (отрезки) на плоскости и в пространстве. Для этого мы будем использовать функции line (используется как в плоскости, так и в пространстве) и plot (для плоскости, для пространства аналогом будет plot 3).
>> help имя команды — позволяет узнать информацию об этой команде.
line([x1; x2],[y1; y2], ‘Color’,’r’,’LineWidth’,4).
Color — цвет, по умолчанию он синий.
LineWidth — толщина линии в пунктах, один пункт равен 1/72 дюйма. По умолчанию ширина линии равна 0.5 пункта.
Ниже в таблице1 приведены обозначения цветов, типов линий и маркеров. Таблица 1 будет полезна не только для функции line , но и для других команд, отвечающих за графику.
Цвет линии и маркера
[код цвета в палитре RGB ]
пятиконечная звезда (pentagram)
шестиконечная звезда (hexagram)
Итак, функция line позволяет строить на координатной плоскости прямые (отрезки) по точкам, координаты которых являются входными аргументами в функцию. Если нам надо изобразить отрезок с началом в точке и концом в точке Мы должны записать в первых квадратных скобках абсциссу начальной точки, затем через точку запятой абсциссу конечной точки, далее через запятую в следующих квадратных скобках аналогичные данные по ординатам. Далее через запятую определённым образом записываются свойства линии (если мы хотим изменить свойства, имеющиеся по умолчанию)
При выполнении упражнений сначала все проделать у себя в тетради, затем в MATLAB.
Упражнение 1. Функция line (тетрадь+ MATLAB )
Построить три отрезка
(0,0)______(2,1) , (0,0)______(-1, 2), (-2,-4)______(0,0) .
Задаём первую прямую (0,0)______(2,1)
с началом в точке и концом в точке ,
задаём аргументы функции line ([0;2],[0;1]),
для второго и третьего отрезков задайте аргументы функции самостоятельно
После ниже следующих команд сразу появится графическое окно Figures. Закрепите окно Figures над Command Window, для этого щелкните левой кнопкой мыши по стрелочке Dock Figure в правом верхнем углу графического окна.
>> line ([0;2],[0;1]), line (), line ()
Для того чтобы легче было воспринимать картинку добавим команды для оформления графика. Включите сетку командой «grid on» и введите одинаковый масштаб по осям «axis equal»
>> grid on, axis equal
В итоге у Вас должно получиться, см. Рис.6.
По умолчанию функция line изобразила отрезки синим цветом.
Скопируйте рисунок в отчёт. Для того чтобы скопировать рисунок в файл, сделайте активным графическое окно, в меню выберете Edit → Copy Figure .
Закройте окно Figures .
Если надо нарисовать несколько прямых в одной команде
(X 10 ,Y 10 )____(X 1 ,Y 1 ),
(X 20 ,Y 20 )_____(X 2 ,Y 2 ),
(X 30 ,Y 30 )_____(X 3 ,Y 4 ),
то нужно записать координаты векторов в определённой последовательности:
line ([абсциссы начал ; абсциссы концов],[ординаты начал; ординаты концов])
line([X 10, X 20, X 30 ; X 1, X 2, X 3 ],[ Y 10 ,Y 20 ,Y 30 ; Y 1, Y 2, Y 3 ])
Для того чтобы всякий раз не закрывать графическое окно, а новый объект изображался в новом графическом окне, перед командами, отвечающими за очередное построение нужно ввести
Упражнение 2. Для самостоятельной работы. (тетрадь+ matlab )
Постройте три отрезка (0,0)____(2,1) , (0,2)_____(2,0) , (0,2)_____(3,0)
с помощью одной команды line .
- Размещение нескольких рисунков в одном графическом окне.
Команда subplot ( n 1, n 2, n ) разбивает графическое окно Figures на несколько графических областей одинакового размера: n 1 — число областей по горизонтали, n 2 — число областей по вертикали, n -выбор области, в которой предстоит строить (в отличии от матриц нумерация идёт по строкам).
Пример 1. Разбиение графического окна на несколько областей.
Создать графическое окно для четырёх координатных плоскостей. В первых трёх построить по одному отрезку, в четвертой все три.
(0,0)______(2,1) , (0,0)______(-1,2), (-2,-4)______(0,0)
>> grid on, axis equal
>> grid on, axis equal
>> grid on, axis equal
>> grid on, axis equal, line([0,0,-2;2,-1,0],[0,0,-4;1,2,0])
Упражнение 3. Для самостоятельной работы (тетрадь+ MATLAB )
Создать графическое окно для четырёх координатных плоскостей. В третьей области построить все три отрезка, в остальных по одному.
(0,0)____(2,1) , (0,2)_____(2,0) , (0,2)_____(3,0) .
- Построение векторов на плоскости.
Если требуется изобразить вектор, то есть отрезок со стрелкой на конце, можно воспользоваться функцией quiver (). Ее формат следующий :
quiver(x_begin, y_begin, x_comp, y_comp, scale, LineSpec),
где x _ begin и y _ begin это массив абсцисс и ординат начал векторов, а x _ comp и y _ comp компоненты векторов. Параметр scale мы будем принмать равным 1.
Функция quiver часто используется для построения большого количества векторов (т. н. векторных полей), где важны не столько длины векторов, сколько их визуальное соотношение. Параметр scale позволяет упростить анализ векторных полей. Однако мы эту функцию используем для точного отображения векторов, поэтому у нас scale всегда равен 1.
Если нужно построить вектора разными цветами, для каждого цвета следует использовать отдельную функцию quiver .
Команды графики, такие как plot, quiver , surf и т.д. стирают предыдущие изображения, включение режима добавления графиков « hold on» позволяет этого избежать.
Пример 2. Векторы на плоскости
Построим следующие векторы:
(0,0)______(2,1) , (0,0)______(-1,2), (0,0)______(-2,-4)
Толщину последнего положим равной 4.
Первые два аргумента функции quiver начало вектора совпадает с первой точкой отрезка. Вторые два аргумента компоненты вектора есть разность начальной и конечной точек отрезка. В данном случае компоненты совпадают с конечной точкой отрезка.
>> figure , grid on , axis equal , hold on
>> quiver(0, 0, 2, 1, 1)
>> quiver(0, 0, -1, 2, 1, ‘g’)
>> quiver(0, 0, -2, -4, 1, ‘r’ , ‘lineWidth’, 4)
Другой способ рисования векторов заключается в последовательном использовании функций line() для рисования отрезка и функции plot ( x , y , > , LineWidth ,4) для рисования стрелки
Координаты x , y в plot — это координаты точки на плоскости (в нашем случае точки конца вектора).
В первых одинарных кавычках можно разместить маркер, цвет, тип линии, в нашем случае размещён только маркер — треугольник, тип линии нам пока не нужен. Команды «^, , v » задают треугольники, которыми удобно помечать концы векторов. « LineWidth » задаёт толщину маркера. См. выше таблицу 1.
Пример 3. Векторы на плоскости (тетрадь+ matlab )
Построим векторы, взяв за их основу отрезки с соответствующими началом и концом:
(0,0)______(2,1) , (0,0)______(-1,2), (0,0)______(-2,-4)
отметив «концы-стрелочки» в соответствующих точках.
При добавлении в функцию line опции « ‘ Color ‘ ,[ код цвета в палитре RGB ]», можно влиять на цвет линии. Цвет выбирается на основании таблицы 3.
>> figure, grid on, axis equal, hold on
>> line([0; -2], [0 -4], ‘lineWidth’, 4, ‘Color’, [1 0 0])
Очевидно, что оба способа рисования векторов подходят только для случая, когда необходимо различать начало и конец отрезка. В случае, когда нужна стрелка указания некоторого элемента на графике, лучше всего воспользоваться сторонней функцией arrow. Скачать её можно здесь . Вот пример реализованного функционала:
Упражнение 4. Для самостоятельной работы. (тетрадь+ matlab )
Построить следующие векторы (0,0)____(2,1), (0,2)_____(2,0),(0,2)_____(3,0). Можно пользоваться quiver и line+plot по выбору. Все векторы покрасить в чёрный цвет, установить толщину 3.
Векторы на графике можно подписать, используя команду text (), входными параметрами в text служат координаты точки, в которой будет стоять надпись, саму надпись пишем в фигурных скобках в одинарных кавычках. Пометим векторы из предыдущего упражнения. Синий будет вектором a , зелёный — b , красный — c .
text (2.5,1.5, ‘ bfa ‘ ) % добавление полужирного обозначения вектора
text (2.5,0.5, ‘ a ‘ ) % добавление обычного обозначения вектора
Добавление перед текстом письма «bf» позволяет сделать текст полужирным, (векторы принято обозначать полужирными буквами). Ниже на рисунке 7 посмотрите разницу между пометками векторов полужирными и обычными буквами.
Для того чтобы в одном выражении написать полужирные и обычные символы, выделяемые полужирным символы заключают в фигурные скобки, например, для того чтобы добавить запись,
c = 1 i 4 j , запишем следующее
- Построение векторов в пространстве.
Для того чтобы в трёхмерном пространстве изобразить стрелки — концы векторов, вместо команды plot ( x , y ) нужно воспользоваться командой plot 3( x , y , z ). Аналогично вместо quiver используется quiver3.
Упражнение 5. Векторы в пространстве (тетрадь+ MATLAB )
Изобразить векторы-орты координатных осей в пространстве:
орты — единичные направляющие векторы
(0, 0, 0) _____________(1, 0, 0)
(0, 0, 0) _____________(0,1, 0)
(0, 0, 0) _____________(0, 0, 1)
После введения необходимых команд у Вас может появиться плоская картинка. Для того чтобы сделать её объёмной, нужно выбрать иконку « Rotate 3 D » на панели инструментов графического окна Figures , затем перевести курсор на график и повращать его, добившись нужного ракурса.
В результате должно получиться что-то похожее на следующий рисунок.
Работа из командной строки MATLAB затрудняется, если требуется вводить много команд и часто их изменять. Самым удобным способом выполнения групп команд MATLAB является использование Мфайлов, в которых можно набирать команды, выполнять их все сразу или частями, сохранять в файле и использовать в дальнейшем. Для работы с Мфайлами предназначен редактор Мфайлов. С его помощью можно создавать собственные функции и вызывать их, в том числе и из командного окна.
Раскройте меню File основного окна MATLAB и в пункте New выберите New Script. Или найдите иконку, открывающую New Script. Появится новое окно редактора Mфайлов, которое изображено на рисунке.
Мфайлы в MATLAB бывают двух типов: файлпрограммы (Script MFiles), содержащие последовательность команд, и файлфункции, (Function MFiles), в которых описываются функции, определяемые пользователем.
Мы пока будем писать программы скрипты (Script MFiles).
Наберите в редакторе команды из последнего упражнения. Сохраните теперь файл с каким-нибудь именем mydemo.m в какомнибудь подкаталоге вашего диска, выбрав пункт Save as меню File редактора. Для запуска на выполнение всех команд, содержащихся в файле, следует выбрать иконку Run (зеленую стрелку) в меню редактора.
Команды файлпрограммы осуществляют вывод в командное окно. Для подавления нежелательного вывода следует завершать команды точкой с запятой. Если при наборе сделана ошибка и MATLAB не может распознать команду, то происходит выполнение команд до неправильно введенной, после чего выводится сообщение об ошибки в командное окно.
Очень удобной возможностью, предоставляемой редактором Мфайлов, является выполнение части команд. Выделите при помощи мыши, удерживая левую кнопку, или клавишами со стрелками при нажатой клавише Shift, первые четыре команды и выполните, нажав клавишу F9.
Так же для частичного выполнения команд можно создавать блоки кода. Строка, которая начинается с двух знаков процента %%, знаменует начало блока. Блок продолжается до следующей строчки с %%, либо до конца файла, если такой строки нет. При перемещении курсора на блок кода блок подсвечивается. Выполнить все команды в подсвеченном блоке можно сочетанием Ctrl + Enter . Некоторые упражнения из этого занятия занимают всего несколько строчек. Их удобно объединить в один скрипт, выделив в блоки кода.
Редактор команд помогает отслеживать критические и некритические ошибки, использование переменных и т.д. К некритической ошибке, например, относится неподавленная точкой запятой команда, которая выведет в командное окно большое количество данных.
Командное окно стоит держать настолько чистым, насколько это возможно, выводя лишь те значения, которые действительно необходимо. Поэтому MATLAB по умолчанию подсвечивает неподавленный вывод как предупреждение. При этом вывод лучше осуществлять не непосредственным обращением к переменной, а с использованием функции disp. Её вывод занимает меньше места и может быть комбинирован с текстом. Например ,
>> disp([‘Escape velocity is equal ‘, num2str(v2), ‘ km/s’]);
Escape velocity is equal 11.2 km/s
Отдельные блоки Мфайла можно снабжать комментариями, которые пропускаются при выполнении, но удобны при работе с Мфайлом. Комментарии начинаются со знака процента и автоматически выделяются зелёным цветом.
Открытие существующего Мфайла производится при помощи пункта Open меню File рабочей среды, либо редактора Мфайлов. Так же можно прописать в консоли
Расширение файла . m указывать не обязательно.
Создание Script MFiles
Все ниже следующие упражнения проделать сначала у себя в тетради, к каждому создать скрипт.
О вызове скриптов. Когда вы вводите имя команды или функции в командной строке, MATLAB ищет файл с данным названием в рабочей папке. Если там его нет, MATLAB последовательно просматривает все папки, отмеченные в системной переменной PATH (это справедливо и для Windows, и для Linux). Поэтому, если попытаться выполнить скрипт через F5, находясь в другой директории, MATLAB предложит либо сменить папку, либо добавить её в переменную PATH. Последнее следует делать только при крайней необходимости. Лучше менять папку.
Упражнение 6. Для самостоятельной работы.
а) Изобразить координатные оси двухмерного пространства X , Y толщиной 2, а орты изобразить черным цветом, толщины 4.
b ) Изобразить координатные оси трёхмерного пространства X , Y , Z толщиной 2, а орты изобразить черным цветом, толщины 4.
Во всех дальнейших упражнениях, даже если это не указано явно, необходимо отображать координатные оси и орты. Теперь, когда вы научились писать скрипты, вводить команды каждый раз заново не нужно достаточно вызвать соответствующий скрипт.
Упражнение 7. Для самостоятельной работы.
Сколько прямых рисует функция line ? Изобразить в тетради и в матлаб данные прямые (отрезки), указать координаты точек конца каждой прямой. С помощью команды axis ([ xmin xmax ymin ymax ]) установить оптимальные границы координатных осей, включить отображение координатной сетки, установить одинаковый масштаб по осям.
Упражнение 8. Правило треугольника.
Изобразить правило треугольника на следующем примере.
Даны три точки с координатами A(-2 0), B(1 2), C(1 -1). Найти векторы АВ, ВС, AC. Убедиться, что АВ+ВС=AC. Изобразить векторы АВ и ВС синим и АС красным, выделить и обозначить вершины (команда text).
Упражнение 9. Правило параллелограмма.
Дан параллелограмм ABCD, известны координаты трёх его точек
A(-2 0), B(1 2), C(1 -1). Найти координаты четвертой вершины D (x,y) параллелограмма.
Разбить графическое окно на две области.
В первом изобразить параллелограмм с помощью line ABCD, выделить и обозначить вершины (команда text)..
Найти векторы AB, DC, AD, BC .
Доказать, что пары векторов AB и DC, AD и BC коллинеарны, сонаправлены и равны.
Во втором графическом окне показать правило параллелограмма:
AB+ AD =AC.
Изобразить векторы АВ и AD синим и АС красным,
остальные стороны параллелограмма ВС и CD -черным.
Упражнение 10. Сумма и разность векторов.
Вычислить суму двух векторов a1=(2;3;4), b1=(3;5;2).
Вычислить разность двух векторов a2=(2;3;4), b2=(3;5;2).
Сделать геометрическую интерпретацию в двух областях одного графического окна. Пометить векторы полужирным шрифтом (команда text, )
Функция isequal( , ). которая возвращает значение 1 (true истина), если сравниваемые величины равны, и 0 (false ложь) в противном случае.
Упражнение 11. Свойства суммы векторов
Проверить свойства суммы векторов, используя векторы
сначала непосредственно, затем используя функцию isequal( , ).
Сделать геометрическую интерпретацию.
Произведением вектора на число назовем вектор , удовлетворяющий следующим трем условиям:
- коллинеарен ;
- ;
- направление совпадает с направлением , если , и противоположно ему, если.
Под произведением вектора на число будем понимать нулевой вектор θ . Напомним, нулевой вектор, в силу его определения, не имеет направления, а длина его равна нулю.
Вектор имеет длину такую же, как вектор (уметь доказывать),
и направление, противоположное направлению (так как число ( 1)
Вектор называется противоположным для вектора .
Свойства умножения вектора на число:
1) распределительное или дистрибутивное свойство;
2) распределительное или дистрибутивное свойство;
3) сочетательное или ассоциативное свойство.
(дистрибутивность от латинского distributivus «распределительный»)
Упражнение 12. Проверить свойства умножения вектора на число.
Даны векторы a=(4,2,3), b=(1,5,2) и числа α=4, β=3.
Длина вектора равна квадратному корню из суммы векторов его координат:
где k номер элемента (координаты) вектора, n общее число элементов в векторе.
Пока у нас будут встречаться геометрические векторы, заданные в декартовой системе координат в плоскости ( n = 2 ) и в пространстве ( n = 3).
Функция sum() позволяет суммировать все элементы вектора, оператор «.*» осуществляет поэлементное умножение векторов, в том числе и вектора самого на себя, функция sqrt() вычисляет корень из значения входного аргумента. Так же для вычисления длины можно использовать встроенную norm ().
Орт вектора единичный вектор , сонаправленный вектору .
Упражнение 13. Длина вектора, орт вектора. Пространство.
Длину вектора = вычислить по определению и с помощью встроенной функции, вычислить орт . Проверить является ли вычисленный вектор единичным. Изобразить оба вектора. Упражнение выполнить, создав соответствующий скрипт.
Упражнение 14. Длина вектора, орт вектора. Плоскость.
Длину вектора = вычислить по определению и с помощью встроенной функции, вычислить орт . Проверить является ли вычисленный вектор единичным. Изобразить оба вектора. Упражнение выполнить, создав соответствующий скрипт.
На протяжении курса нам ещё не раз встретятся случаи, когда для вычисления той или иной величины в MATLAB уже имеется встроенная функция. Однако чем сложнее алгоритм, тем больше вероятность, что встроенная функция реализует его вариацию, либо слишком частный, либо слишком общий случай (последнее плохо сказывается на производительности). Поэтому в каждом конкретном случае следует чётко представлять себе, что должно быть на выходе и проверять работу функции на известных примерах. Писать свою реализацию имеет смысл только в том случае, когда встроенная вас не удовлетворяет.
Пусть дан геометрический вектор . Обозначим углы наклона этого вектора к осям Ox, Oy, Oz соответственно через α, β, γ. Три числа cos α,cos β, cos γ являются направляющими косинусами вектора . Направляющие косинусы вычисляются по формулам
а значит, являются координатами орта .
Сумма квадратов направляющих косинусов любого вектора равна единице
Пусть дан геометрический вектор . Обозначим углы наклона этого вектора к осям Ox, Oy соответственно через α, β. Два числа cos α,cos β являются направляющими косинусами вектора . Направляющие косинусы вычисляются по формулам
а значит, являются координатами орта .
Сумма квадратов направляющих косинусов любого вектора равна единице
Для непосредственного вычисления углов наклона вектора в градусах нужно использовать
Упражнение 16. Направляющие косинусы. Орт вектора. Пространство.
Вычислить в градусах углы наклона вектора =(3,4,5) к осям координат.
Проверить, что сумма квадратов направляющих косинусов вектора будет равна единице. Не забудьте перевести градусы обратно в радианы.
Упражнение 17. Направляющие косинусы. Орт вектора. Плоскость.
Вычислить в градусах углы наклона вектора =(2,4) к осям координат.
Проверить, что сумма квадратов направляющих косинусов вектора будет равна единице. Не забудьте перевести градусы обратно в радианы.
- Линейная зависимость векторов
Линейной комбинацией векторов с коэффициентами будем называть конечную сумму вида
Линейная комбинация называется нетривиальной, если хотя бы один из ее коэффициентов отличен от нуля.
Определение. Векторы называются линейно зависимыми, если существует нетривиальная линейная комбинация из этих векторов, равная нулевому элементу : .
Простейшие примеры линейно зависимых векторов.
1. Вектор и его противоположный вектор составляют линейно зависимую систему векторов.
таким образом, и система векторов , линейно зависима.
2. Коллинеарные векторы (уметь доказывать)
3. Компланарные векторы (уметь доказывать)
4. Любые n () геометрических вектора.
Пример. Составим линейную комбинацию из векторов
, и .
. Задача найти коэффициенты линейной комбинации
Очевидно, что решением здесь будут коэффициенты .
Система векторов называется линейно независимой, если из равенства следует, что все коэффициенты равны нулю (то есть существует только тривиальное решение).
Пример. Составим линейную комбинацию из векторов , и
Здесь существует, только тривиальное решение. Эта линейная комбинация может равняться нулевому элементу, только если все коэффициенты равны нулю одновременно.
Два неколлинеарных вектора плоскости составляют базис векторов плоскости. Это означает, что каждый вектор этой плоскости однозначно разлагается по векторам
Некомпланарные векторы образуют базис векторов трёхмерного пространства, и любой вектор пространства может быть единственным образом представлен в виде: .
Упражнение 18. Изобразить векторы базиса. Пространство.
Векторы , и образуют базис (показать, что векторы некомпланарны).
Изобразить эти векторы (в виде прямых) с помощью функций line и plot3.
Изобразить орты черным цветом, толщиной LineWidth, 4
Вычислить и изобразить орты векторов толщиной LineWidth,4
Упражнение выполнить, создав соответствующий скрипт.
Сразу ввести команды для оформления графика, написать комментарии к ним:
grid on % что выполняют эти команды?
hold on % что выполняют эти команды?
xlabel (‘ X ‘), ylabel (‘ Y ‘), zlabel (‘ Z ‘) %
Упражнение 19. Изобразить векторы базиса. Плоскость.
Векторы p = и q = образуют базис (показать, что векторы неколлинеарны). Найти разложение вектора s = по базису p и q : s =m p + n q . Изобразить векторы p , q , m p , n q , s , а также координатные оси Ox и Oy и орты i , j .
Упражнение выполнить, создав соответствующий скрипт
Упражнение 20. Разложение вектора по двум неколлинеарным векторам.
На плоскости даны три вектора a = , b = , c = . Определить разложение каждого из этих трёх векторов, принимая в качестве базиса два других. Графическое окно разбить на четыре области. Во всех окнах изобразить координатные оси Ox и Oy, орты i , j . В первой изобразить три вектора. В оставшихся трёх геометрическую интерпретацию разложения каждого из этих трёх векторов по двум остальным. Векторы базиса представлять синим цветом, разлагаемый вектор красным.
Упражнение 21. Разложение вектора по трем некомпланарным векторам.
Письменно и используя графические средства MATLAB проверить векторы на компланарность и, если они некомпланарны, разложить вектор по трем некомпланарным векторам : , считая ортами прямоугольной декартовой системы координат, изобразить некомпланарные векторы черным цветом, толщиной LineWidth, 4, а также векторы и вектор .
( коэффициенты разложения неизвестные в соответствующей системе уравнений)
B) , и ,
Упражнение выполнить, создав соответствующие скрипты.
Упражнение 22. Линейная зависимость четырёх векторов.
Даны четыре вектора a = , b = , c = и d = . Определить разложение каждого из этих четырёх векторов, принимая в качестве базиса три остальных. Сделать геометрическую интерпретацию задачи на отдельных четырёх рисунках. Команда figure перед командами, отвечающими за графику, позволяет открывать новое графическое окно. На первом рисунке изобразить координатные оси, орты осей и четыре вектора. На оставшихся трёх геометрическую интерпретацию разложений. Векторы базиса представлять синим цветом, разлагаемый вектор красным.
- Косоугольная и прямоугольная система координат.
В результате выполнения упражнения 2 можно получить примерно следующее.
На первом рисунке мы видим разложение вектора s по прямоугольному декартовому базису , в котором базис суть орты (единичные векторы), причём взаимно перпендикулярные. Прямоугольную систему координат и прямоугольную декартову системы координат следует различать. В прямоугольной системе координат векторы базиса, будучи ортогональными, не обязаны быть единичными.
На втором рисунке мы видим разложение того же вектора s в базисе векторов ( p , q ), которые не единичны и не взаимно перпендикулярны. Векторы p и q приведённые к общему началу образуют косоугольную систему координат.
- Скалярное произведение векторов
Нумерацию формул и рисунков начнём заново.
Определение 1. Скалярным произведением векторов и называется число
Геометрические свойства скалярного произведения даются теоремами 1 и 2.
Теорема 1. Два вектора и ортогональны (перпендикулярны) тогда и только тогда, когда их скалярное произведение равно нулю.
Условие перпендикулярности двух векторов выглядит так:
Скалярное произведение может быть использовано для проверки или
для доказательства перпендикулярности векторов.
Упражнение 23. Условие ортогональности векторов.
Найти все векторы, перпендикулярные вектору . Изобразить эти векторы.
Теорема 2. Для любых двух векторов и , если , , угол является острым тогда и только тогда, когда , и тупым тогда и только тогда, когда .
Алгебраические свойства скалярного произведения:
Алгебраические свойства дают возможность, перемножая линейные комбинации векторов, группировать коэффициенты, как при перемножении многочленов.
Замечание 1 . Свойства 2 и 3 справедливы также в форме:
Упражнение 24.1 . Свойства скалярного произведения векторов.
Даны векторы , и . Используя функцию isequal , проверить свойства 1, 2, , 3, , 4 скалярного произведения векторов.
Скалярное произведение векторов обладает многими свойствами, которыми обладает произведение действительных чисел. Однако, автоматическое (бездумное) перенесение на векторы свойств действительных чисел, которыми векторы не обладают, является ошибочным. В частности, для векторов несправедлив закон ассоциативности (сочетательный закон), т.е. в общем случае
Упражнение 24.2. Свойства скалярного произведения векторов.
Даны векторы , и . Используя функцию isequal , убедиться в невыполнении равенств (2), (3), (4).
Приведём ещё примеры. 1) если векторы, изображённые на рисунке 2, то но 2) для векторов на рисунке 3 но
Упражнение 25. Для самостоятельной работы.
Составить задачи с конкретными векторами, иллюстрирующие рис.1 и рис.2, а также показать для первой задачи, что но
для второй но
Пример 1. Вычисление скалярного произведения в декартовом базисе.
Пусть , декартов базис , a =3 i +4 j , b =2 i — j .
Найти скалярное произведение( a , b ), длины векторов a и b .
( a , b )=(3 i +4 j ,2 i j )=(3 i ,2 i j )+(4 j ,2 i j )=(3 i ,2 i )+(3 i , j )+(4 j ,2 i )+(4 j , j )=
=3*2*( i , i ) 3( i , j )+8( j , i ) +4*(-1)*( j , j )=6( i , i )+5( i , j )-4( j , j )=3*2+5*4*1=
если придать вычислениям общий вид: a = a 1 i + a 2 j , b = b 1 i + b 2 j , получим:
— формула для вычисления скалярного произведения в координатной форме.
( a , a )=(3 i +4 j ,3 i +4 j )=9( i , i )+24( i , j )+16( j , j )=3*3+24*0+4*4=25.
если придать вычислениям общий вид, получим:
— скалярный квадрат равен квадрату длины вектора.
— длина вектора корень из суммы квадратов координат вектора.
( b , b )=( 2 i — j , 2 i — j )= 4( i , i )-4( i , j )+( j , j )=4*1*1-4*1*1*+1*1=4+0+1=5.
если придать вычислениям общий вид, получим:
Так как базис декартов, то есть состоит из двух единичных взаимно перпендикулярных векторов. То скалярное произведение орта самого на себя будет равно единице, т.к. длины векторов раны единице, и , произведение взаимно перпендикулярных ортов равно нулю.
В косоугольной системе координат решения и ответы будут другие.
Пример 2. Вычисление скалярного произведения в косоугольном базисе, состоящем из единичных векторов.
Пусть p и q косоугольный базис , векторы длины один,
а угол между ними равен 60 о , a =3 p +4 q , b =2 p — q .
Найти скалярное произведение ( a , b ) , длины векторов a и b ..
( a , b )=(3 p +4 q ,2 p — q )=(3 p ,2 p — q )+(4 q ,2 p — q )=(3 p ,2 p )+(3 p ,- q )+(4 q ,2 p )+(4 q ,- q )=
=6( p , p )-3( p , q )+8( q , p )-4( q , q )=6( p , p )+5( p , q )+4( q , q )=6+5-4 =6+5/2-4=4,5
если придать вычислениям общий вид: a = a 1 p + a 2 q , b = b 1 p + b 2 q , получим:
*- формула для вычисления скалярного произведения в координатной форме изменилась.
( a , a )=( 3 p +4 q , 3 p +4 q )= 9( p , p )+2*12*( p , q )+16( q , q )=9+2*12*+16=37.
— скалярный квадрат по-прежнему равен квадрату длины вектора,
но вычисляются они теперь по-другому.
( b , b )=( 2 p — q , 2 p — q )= 4( p , p )-4( p , q )+( q , q )=4-2*2*+1=3.
Пример 3. Вычисление скалярного произведения в косоугольном базисе, состоящем из векторов произвольной длины.
Пусть p и q косоугольный базис , причем длины векторов равны 2 и 3 соответственно, а угол между ними равен 60 о , a =3 p +4 q , b =2 p — q .
Найти скалярное произведение ( a , b ) , длины векторов a и b ..
( a , b )=(3 p +4 q ,2 p — q )=(3 p ,2 p — q )+(4 q ,2 p — q )=(3 p ,2 p )+(3 p ,- q )+(4 q ,2 p )+(4 q ,- q )=
=6( p , p )-3( p , q )+8( q , p )-4( q , q )=6( p , p )+5( p , q )+4( q , q )=6*2*2+5*2*3* 4*3*3= =24+15 36=3
если придать вычислениям общий вид: a = a 1 p + a 2 q , b = b 1 p + b 2 q , получим:
+ *- формула для вычисления скалярного произведения в координатной форме снова изменилась.
( a , a )=( 3 p +4 q , 3 p +4 q )= 9( p , p )+24( p , q )+16( q , q )=
( b , b )=( 2 p — q , 2 p — q )= 4( p , p )-4( p , q )+( q , q )=4*2*2-4*2*3*+3*3=13.
В примерах 1,2 и 3 показано как усложняются расчеты вычисления скалярного произведения векторов и длины вектора в косоугольной системе координат по сравнению с декартовой прямоугольной системой координат.
- Скалярное произведение в координатной форме
Выше в примерах 1,2,3 мы фактически предвосхитили тему данного параграфа.
Теорема 3. Пусть ,, декартов базис , , .
Тогда .
Следствие. Пусть ,, декартов базис , , , , . Тогда
В самом деле, из формулы (2.1), определяющей скалярное произведение, находим
и соотношение (5) доказано.
Скалярное произведение двух векторов a и b заданных в координатной форме в MATLAB мы будем вычислять различными способами:
1. Создать формулу, обращаясь индексами к элементам массива
2. Вычислить с помощью поэлементного умножения «.*» произведения соответствующих координат, убедиться, что вычисления соответствуют ожидаемым, затем применить к результату функцию sum .
3. Затем сразу применить обе операции ab = sum ( a .* b ).
4. В matlab есть стандартная функция, вычисляющая скалярное произведение dot ()
Упражнение 26. Скалярное произведение в координатной форме.
Вычислить скалярное произведение двух векторов a = , b =
>> syms x1 x2 y1 y2 z1 z2
>> a =[ x 1, y 1, z 1]; b =[ x 2, y 2, z 2];
Далее самостоятельно:1,2 3 и 4 способы.
Упражнение 27. Скалярное произведение в прямоугольном и косоугольном базисе.
Выразить скалярное произведение векторов , , то есть ,
A ) в декартовом базисе , и
B ) косоугольном базисе , и . Пользуясь геометрическим свойством скалярного произведения, убедиться, что векторы a , b , c образуют косоугольный базис.
C ) в прямоугольном, но не в ортонормированном базисе, и
Определение скалярного произведения через понятие проекции.
Заметим, что в формуле (1) ,
если принять за орт вектора ,
поэтому можно дать определение скалярного произведения и в иной, равносильной форме, иногда более удобной.
Определение . Скалярным произведением векторов и называется число, равное проекции одного вектора на другой, умноженной на длину последнего.
Упражнение 28. Определение скалярного произведения через понятие проекции.
Пусть , декартов базис , a =3 i +4 j , b =2 i — j . Сделать геометрическую интерпретацию, определения .
- Задание для самостоятельной работы
1. Выполнить в тетради и в MATLAB все упражнения данного практикума.
2. Ответить на контрольные вопросы (некоторые темы изучить самостоятельно). Уметь отвечать на вопросы по темам лабораторной работы и по темам презентаций, даже если презентацию вы не готовите.
3. Подготовить краткую презентацию (57 минут) с применением графических средств MATLAB , и выступить с ней у доски. Презентация должна включать в себя вопросы к аудитории.
Темы для презентаций:
1) Орт вектора, направляющие косинусы вектора.
2) Расстояние между векторами.
3) Проекция вектора на ось, свойства, декартов базис.
4) Физический смысл скалярного произведения (найти, рассказать)
Задачи для презентаций:
1. Танковый биатлон.
Ведется огонь по некоторой цели. Цель представляет собой стальной плоский лист толщиной 200 мм, внешняя поверхность листа лежит на плоскости ZY . Координаты орудия в метрах , огонь ведётся по точке (в метрах). Найти толщину листа по прямолинейной траектории полета снаряда от момента вхождения в цель до момента выхода из цели. Для решения задачи создать скрипт, в котором можно быстро изменить входные параметры.
2. Заданы начало и конец отрезка. Необходимо нарисовать стрелку с усиками, ширина раствора которых равна w , а высота h (см. рисунок). Тригонометрию использовать нельзя (подобное ограничение часто возникает во встраиваемых системах, где вычисление тригонометрических функций слишком дорого по времени). Проиллюстрировать скриптом в матлабе.
1. Как осуществляется построение нескольких графиков в одном графическом окне?
2. Как создать графическое окно с несколькими графическими окнами?
3. Как нанести измерительную сетку на всю область построения графика?
4. Как установить границы координатной сетки?
5. Что построят данные команды
в) line ([0 0 0;-1 0 0],[0 0 0;0 -1 0],[0 0 0;0 0 -1] ?
Записать начало и конец каждого отрезка, построить отрезки в виде векторов, не используя MATLAB , в MATLAB выполнить построение соответствующих векторов.
6. Что происходит с элементами векторов, при суммировании и вычитании векторов, заданных в координатной форме?
7. В каком ещё окне рабочего пространства кроме Command Window. можно набирать формулы или команды, удовлетворяющие синтаксису языка MATLAB?
8. Какую роль играет оператор «…».
9. Как осуществить построение нескольких графиков в различных окнах? (подсказка: изучить команду figure)
10. Как устроена функция isequal( , )?
11. Как в теле одного скрипта можно создать несколько графических окон?
12. Какова связь между ортом вектора и его направляющими косинусами. Какова длина орта вектора? Какова длина вектора, координаты которого раны направляющим косинусам? Доказать и .
13*. Проекция вектора на ось. Как связаны понятие проекции и происхождение прямоугольного декартового базиса?
14. Какие векторы называют коллинеарными, необходимое и достаточное условие линейной зависимости двух векторов. Условие коллинеарности для координат векторов (выражение условия коллинеарности в координатной форме)
15. Какие векторы называют компланарными, необходимое и достаточное условие линейной зависимости трёх векторов?
16. Скалярное произведение векторов определение, способы вычисления в MATLAB .
17. Как определяется длина вектора через скалярный квадрат? Найти скалярный квадрат вектора a =. Определить длину вектора a .
18. Скалярное произведение векторов в координатной форме и его свойства.
19. Как определяется угол между векторами? Вычислить угол между векторами a = и b =.
20. Ответить на вопросы, заданные в виде теста, выбор ответов обосновать
(в тетради и в отчёте , привести примеры из MATLAB ).
1. Угол между векторами
a =[ x 1, y 1, z 1] и b =[ x 2, y 2, z 2]
вычисляется по формуле в MATLAB
Как ещё можно найти угол между векторами?
2. Проекция вектора a =[ x 1, y 1, z 1] на вектор b =[ x 2, y 2, z 2] вычисляется по формуле в MATLAB
Почему в формуле необходимо транспонировать один из векторов? Как еще можно найти проекцию?
3. Ненулевые векторы
a =[ x 1, y 1, z 1] и b =[ x 2, y 2, z 2]
коллинеарные, если в MATLAB
А) ( a ./ b ).* b совпадет с a
Б) ( b ./ a ).* a совпадет с b
Г) ( b ./ a ).* a совпадет с a
4. Ненулевые векторы
a =[ x 1, y 1, z 1] и b =[ x 2, y 2, z 2]
ортогональны, если в MATLAB
А) ( a * b ‘) даст 0
Б) dot ( a , b ) даст ответ ±1.
В) ( b * a ‘) даст 0
Г) dot ( a , b ) даст ответ 0.
- Контрольное мероприятие № 1. Защита л.1.1 и л.1.2.
Состоится на 5 неделе.
Список вопросов для студентов по КМ 1
Часть 1. Работа с системой MATLAB
Устройство функции « line ».
Часть 2. Теоретическая основа. Контрольные вопросы
(здесь есть вопросы, которые в практикуме не рассматривались, но знать надо)
- Геометрический вектор. Свободный вектор. Закрепленный вектор. Нулевой вектор. Коллинеарные векторы. Равные векторы.
- Коллинеарные векторы. Равные векторы. Компланарные векторы.
- Правила сложения векторов. Применимость этих правил к коллинеарным векторам. Свойства операции сложения геометрических векторов. Правило трех точек.
- Умножение вектора на число. Свойства умножения вектора на число.
- Длина вектора? Орт вектора. Определить длину вектора a =, найти орт вектора.
- Направляющие косинусы и орт вектора ( плоскость)
- Направляющие косинусы и орт вектора ( пространство)
- Линейная комбинация. Определения линейной зависимости и линейной независимости векторов. Четыре простейших примера линейно зависимых векторов.
- Линейная комбинация. Определения линейной зависимости и линейной независимости векторов. Какие векторы образуют базис на плоскости. Сформулируйте необходимое и достаточное условие линейной зависимости двух геометрических векторов.
- Линейная комбинация. Определения линейной зависимости и линейной независимости векторов. Какие векторы образуют базис в пространстве. Сформулируйте необходимое и достаточное условие линейной зависимости трех геометрических векторов.
- Дайте определение базиса и координат вектора в пространстве геометрических векторов V 3.
- Скалярное произведение векторов. Условие перпендикулярности двух векторов.
- Четыре алгебраических свойства скалярного произведения.
- Скалярное произведение векторов, алгебраические и геометрические свойства.
- Косоугольный, прямоугольный, декартов базис.
- Скалярное произведение векторов в координатной форме в косоугольном и декартовом базисах.
- Как определяется угол между векторами? Вычислить угол между векторами a = и b =.
- Проекция вектора на ось и декартовы координаты. Сформулируйте теорему о геометрическом смысле декартовых координат вектора.
- Определение скалярного произведения через понятие проекции. Сделать рисунки.
1. Сколько прямых рисует функция line ( )? Изобразить данные прямые (отрезки), указать координаты точек начала и конца каждой прямой.
2. Длина вектора? Орт вектора. Определить длину вектора a =, найти орт вектора.
1. Сколько прямых рисует функция line ( )? Изобразить данные прямые (отрезки), указать координаты точек начала и конца каждой прямой.
2. Направляющие косинусы и орт вектора (плоскость)
Индивидуальные задания № 1 Векторная алгебра.
Задания разного уровня сложности.
Задачи необходимо иллюстрировать в MATLAB
1. Дан правильный шестиугольник Точка середина стороны Выразить вектор через векторы
2. В параллелограмме и середины сторон и соответственно. Выразить вектор через векторы
3. В треугольнике биссектриса угла Выразить вектор через векторы и длины этих векторов.
4. Пусть точка пересечения медиан треугольника Вычислить сумму
5. Дан правильный шестиугольник Точка середина стороны Разложить вектор по базису
6. На сторонах треугольника соответственно взяты точки и такие, что Пусть точка пересечения отрезков и Разложить вектор по базису
7. Доказать, что высоты треугольника пересекаются в одной точке.
Указание . Пусть и высоты, пересекающиеся в точке Утверждение будет доказано, если мы покажем, что Переформулируем нашу задачу на языке скалярного произведения:
8. В треугольнике проведена высота Выразить вектор через векторы
Вычислить: 1) 2) 3) 4) 5)
Следующие две задачи наглядно показывают возможности скалярного произведения для решения задач элементарной геометрии. Например, для нахождения длин отрезков и для вычисления углов между скрещивающимися прямыми.
10. Все рёбра правильной треугольной призмы равны 1. Найти угол между скрещивающимися диагоналями двух боковых граней призмы.
Решение (см. рис. 17).
11. Все грани параллелепипеда ромбы со стороной 1 и углом Найти наибольшую диагональ параллелепипеда.
- Дан правильный шестиугольник Точка середина стороны Выразить вектор через векторы
- Точка центр правильного шестиугольника Выразить вектор через векторы
- В треугольнике Из точки опущена высота Разложить вектор по базису
- В треугольнике проведены медианы и пересекающиеся в точке Разложить вектор по базису
- В параллелограмме точка середина стороны Разложить вектор по базису
- Доказать, что в любой трапеции следующие 4 точки лежат на одной прямой: середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон.
- Пусть точка пересечения медиан треугольника а произвольная точка. Доказать, что
- Пусть и треугольники, и точки пересечения медиан этих треугольников соответственно. Выразить вектор через векторы и
- Дан параллелепипед Разложить вектор по базису
- Список рекомендуемой литературы
- А. Кривелёв. Основы компьютерной математики с использованием системы MatLab . М, 2005.
- В.А.Ильин, Э.Г.Позняк. Аналитическая геометрия. М.,Наука,2001, Шифр — 514.12(075.8) И-46.
- Ржавинская Е.В., Соколова Т.В., Олейник Т.А. Лекции по линейной алгебре и аналитической геометрии, М.,МИЭТ. 2007.
- Сборник задач по математике для втузов под редакцией А.В.Ефимова, А.С.Поспелова. В 4 частях. Часть 1.(4-е изд. перераб. и доп.)2001, 2004.
- А. Кривелёв. Основы компьютерной математики с использованием системы MatLab . М, 2005.
Видео:Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

Доказать, что 3 вектора образуют базис трёхмерного пространства и найти координаты 4-го вектора в данном базисе
Даны векторы 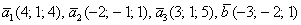

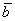
Решение: Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора 

Вычислим определитель, составленный из координат векторов 
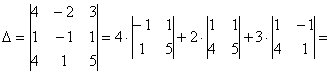
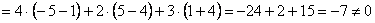

! Важно: координаты векторов 
Теперь вспомним теоретическую часть: если векторы 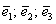
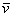
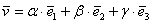
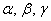
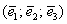
Поскольку наши векторы 
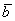
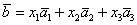
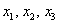
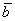
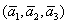
По условию и требуется найти координаты 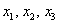
Для удобства объяснения поменяю части местами: 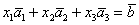
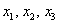
По какому принципу расставлены коэффициенты? Все коэффициенты левой части в точности перенесены из определителя 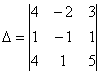
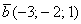
Получилась система трёх линейных уравнений с тремя неизвестными. Обычно её решают поформулам Крамера, часто даже в условии задачи есть такое требование.
Главный определитель системы уже найден:
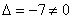
Дальнейшее – дело техники:
Таким образом:
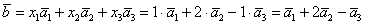
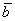
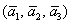
Ответ:
Как я уже отмечал, задача носит алгебраический характер. Векторы, которые были рассмотрены – это не обязательно те векторы, которые можно нарисовать в пространстве, а, в первую очередь, абстрактные векторы курса линейной алгебры. Для случая двумерных векторов можно сформулировать и решить аналогичную задачу, решение будет намного проще. Однако на практике мне такое задание ни разу не встречалось, именно поэтому я его пропустил в предыдущем разделе.
Такая же задача с трёхмерными векторами для самостоятельного решения:
Даны векторы 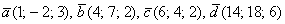
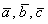
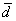
Полное решение и примерный образец чистового оформления в конце урока.
Аналогично можно рассмотреть четырёхмерное, пятимерное и т.д. векторные пространства, где у векторов соответственно 4, 5 и более координат. Для данных векторных пространств тоже существует понятие линейной зависимости, линейной независимости векторов, существует базис, в том числе, ортонормированный, разложение вектора по базису. Да, такие пространства невозможно нарисовать геометрически, но в них работают все правила, свойства и теоремы двух и трех мерных случаев – чистая алгебра. Собственно, о философских вопросах меня уже пробивало поговорить в статье Частные производные функции трёх переменных, которая появилась раньше данного урока.
Любите векторы, и векторы полюбят вас!
Решения и ответы:
Пример 2: Решение: составим пропорцию из соответствующих координат векторов:
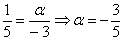
Ответ: при
Пример 4: Доказательство: Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
1) Проверим параллельность противоположных сторон 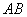
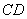
Найдём векторы:
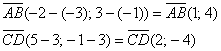
Вычислим определитель, составленный из координат векторов 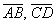
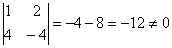
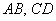
2) Проверим параллельность противоположных сторон 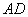
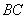
Найдём векторы:
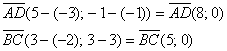
Вычислим определитель, составленный из координат векторов 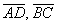

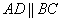
Вывод: Две стороны четырёхугольника 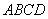
Пример 5: Решение:
б) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов:
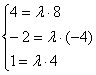
Система не имеет решения, значит, векторы 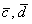
Более простое оформление:
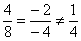
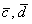
Ответ: векторы 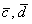
в) Исследуем на коллинеарность векторы 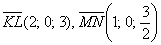
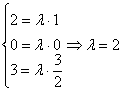
Соответствующие координаты векторов пропорциональны, значит 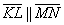
Вот здесь как раз не проходит «пижонский» метод оформления.
Ответ:
Пример 6: Решение: б) Вычислим определитель, составленный из координат векторов 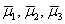
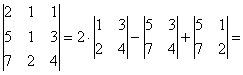
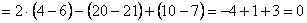
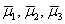
Ответ: данные векторы не образуют базиса
Пример 9:Решение:Вычислим определитель, составленный из координат векторов 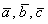

Таким образом, векторы 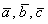
Представим вектор 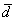
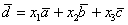
Покоординатно:
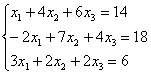
Систему решим по формулам Крамера:
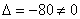
Ответ: Векторы 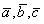
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Векторное произведение векторов.
Смешанное произведение векторов
На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов. Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов, требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение, даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урокаВекторы для чайников, чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы, а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
📹 Видео
#вектор Разложение вектора по ортам. Направляющие косинусыСкачать

Видеоурок "Разложение вектора по базису"Скачать

Написать разложение вектора x по векторам p, q, r. Разложение вектора по базису из трёх векторов.Скачать

Базис. Разложение вектора по базису.Скачать

Образуют ли данные векторы базисСкачать

10 класс, 45 урок, Разложение вектора по трем некомпланарным векторамСкачать

Разложить вектор m по векторам a,b,cСкачать

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Основы линейной алгебры. 2. Векторы. Часть 1Скачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

РАЗЛОЖЕНИЕ ВЕКТОРА по трем векторамСкачать

9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

Что такое векторный базис? Душкин объяснитСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать