Разложить в базисе е1 е2 следующие векторы ав вс са (6 видео)

Разложение вектора по базису

Вектор является элементом векторного пространства. Коллинеарные векторы принадлежат одной или двум параллельным прямым. Могут быть противо- и сонаправленными. Из произвольно выбранной точки в пространстве можно отложить любой вектор одним способом.

Базис плоскости – два неколлинеарных вектора, то есть – линейно независимых. Следует понимать, что любой вектор заданной плоскости представляет собой линейную комбинацию базисных векторов. Если есть два заданных на плоскости неколлинеарных вектора, то любой иной вектор, принадлежащий этой же плоскости, можно разложить по первым двум, то есть – по базису. Для осуществления операции можно воспользоваться онлайн-калькулятором. Это упростит задачу.

Содержание

Математический портал
Nav view search
Navigation
Search
Базис линейного пространства. Разложение вектора по базису.
Разложить вектор по базису онлайн
🔥 Видео

Видео:Найдите разложение вектора по векторам (базису)Скачать

Математический портал

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Nav view search

Search

Вы здесь:
Home

Видео:Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

Базис линейного пространства. Разложение вектора по базису.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Упорядоченная тройка некомпланарных векторов $e_1, e_2, e_3$ называется базисом в пространстве всех геометрических векторов. Всякий геометрический вектор $a$ может быть представлен единственным образом в виде $$a=X_1e_1+X_2e_2+X_3e_3.qquadqquadqquadqquadqquad (1)$$ Числа $X_1, X_2, X_3$ называются координатами вектора в базисе $B=.$ Запись (1) называют разложением вектора $a$ по базису $B.$

Аналогично, упорядоченная пара неколлинеарных векторов $e_1, e_2$ называется базисом $B=(e_1, e_2)$ в множестве геометрических векторов, компланарных некоторой плоскости.

Наконец, всякий ненулевой вектор $e$ образует базис $B=(e)$ в множестве геометрических векторов, коллинеарных некоторому направлению.

Если вектор $a$ есть линейная комбинация векторов $a_1, a_2, . a_n$ с коэффициентами $lambda_1, lambda_2, . lambda_n$, то есть $$a=sumlimits_^n lambda_ka_k$$ то каждая координата $X_i(a)$ вектора $a$ равна сумме произведений коэффициентов $lambda_1,lambda_2. lambda_n$ на одноименные координаты векторов $a_1, a_2, . a_n: $ $$X_i(a)=sumlimits_^nlambda_k X_i(a_k),qquad (i=1, 2, 3.)$$

Базис $B=(e_1, e_2, e_3)$ называется прямоугольным, если векторы $e_1, e_2$ и $e_3$ попрано перпендикулярны и имеют единичную длину. В этом случае приняты обозначения $$e_1=i;,, e_2-j;,, e_3=k.$$

Примеры.

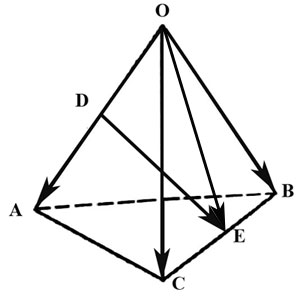
2.26. Задан тетраэдр $OABC.$ В базисе из ребер $overline, overline$ и $overline$ найти координаты:

а) вектора $overline,$ где $D$ и $E$ середины ребер $OA$ и $BC.$

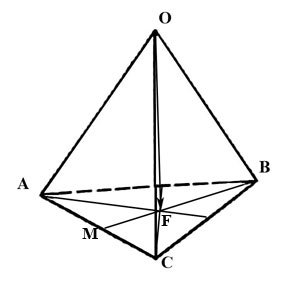
б) вектора $overline,$ где $F-$ точка пересечения медиан основания $ABC.$

Решение.

а)

Выразим вектор $overline$ через вектора $overline, overline, overline:$

Из треугольника $ODE$ имеем $overline=overline+overline.qquadqquadqquad (1)$

вектор $overline$ найдем из треугольника $OBE:$

здесь $overline=fracoverline,$ а вектор $overline$ находим из треугольника $OBC:$

Таким образом, из (2) получаем $overline=overline+frac(overline-overline).$

Наконец из (1) имеем $$overline=overline+overline=-fracoverline+overline+frac(overline-overline)=$$ $$=-fracoverline+fracoverline+fracoverline.$$

Таким образом, координаты вектора $overline$ в базисе из ребер $overline, overline, overline:$ $left(-frac,frac,fracright).$

Ответ: $left(-frac; frac; fracright).$

б)

Выразим вектор $overline$ через вектора $overline, overline, overline:$

Из треугольника $OFB$ имеем $overline=overline+overline.qquadqquadqquad (1)$

вектор $overline$ найдем из треугольника $BMC:$

здесь $overline=fracoverline,$ а вектор $overline$ находим из треугольника $OCA:$

Таким образом, из (2) получаем $$overline=overline+overline=overline-overline+fracoverline=$$ $$=overline-overline+frac(-overline+overline).$$

Наконец из (1) имеем $$overline=overline+overline=overline+fracoverline=$$ $$=overline+fracleft(overline-overline+frac(-overline+overline)right)=$$ $$=overline+fracoverline-fracoverline+frac(-overline+overline)=fracoverline+fracoverline+fracoverline.$$

Таким образом, координаты вектора $overline$ в базисе из ребер $overline, overline, overline:$ $left(frac; frac; fracright).$

Ответ: $left(frac; frac; fracright).$

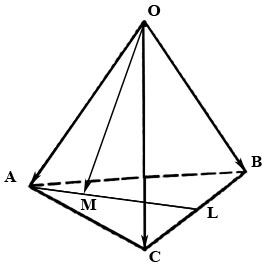
2.27. В тетраэдре $OABC$ медиана $AL$ грани $ABC$ делится точкой $M$ в отношении $|overline|:|overline|=3:7.$ Найти координаты вектора $overline$ в базисе из ребер $overline, overline, overline.$

Решение.

Вектор $overline$ найдем из треугольника $AOM:$ $$overline=overline+overline.qquadqquadqquad (1)$$

Из условия $|overline|:|overline|=3:7$ имеем $overline=fracoverline.$ Из треугольника $ABL$ находим $overline=overline+overline=overline+fracoverline.$

Далее, из треугольников $AOB$ и $BOC$ получаем

Отсюда и из (1) получаем $$overline=overline+overline=overline+fracoverline+fracoverline+fracoverline=$$ $$=fracoverline-fracoverline+fracoverline.$$

Ответ: $left(frac; frac;fracright).$

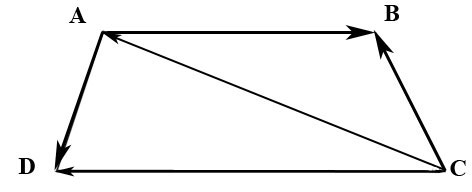
2.29. В трапеции $ABCD$ известно отношение длин оснований $|overline|/|overline|=lambda$ Найти координаты вектора $overline$ в базисе из векторов $overline$ и $overline.$

Решение.

Вектор $overline$ можно найти из треугольника $ABC:$ $overline=overline+overline.$

$overline$ находим из треугольника $ACD:$ $overline=overline+overline=overline-overline.$

Из условия $|overline|/|overline|=lambda$ находим вектор $overline:$ $overline=-overline/lambda.$

Таким образом, $overline=-overline/lambda-overline;$

2.36. Заданы векторы $e(-1, 1, 1/2)$ и $a(2, -2, -1).$ Убедиться, что они коллинеарны и найти разложение вектора $a$ по базису $B(e). $

Решение.

Векторы коллинеарны, если их направления совпадают или противоположны, т.е. тогда и только тогда когда их координаты пропорциональны. Проверим: $$frac=frac=frac=-frac,$$ то есть векторы $e$ и $a$ коллинеарны.

Найдем разложение вектора $a$ по базису $B(e),$ то есть найдем такое число $lambda$ что $a=lambda e:$

Ответ: $a=-2e.$

Домашнее задание.

2.28. Вне плоскости параллелограмма $ABCD$ взята точка $O.$ В базисе из векторов $overline, overline$ и $overline$ найти координаты:

а) вектора $overline$ , где $M$ точка пересечения диагоналей параллелограмма;

б) вектора $overline,$ где $K$- середина стороны $AD.$

Ответ: а) $(1/2; 0; 1/2);$ б) $(1, -1/2, 1/2).$

2.31. В треугольнике $ABC$ $overline=alphaoverline; overline=betaoverline;$ $overline=gammaoverline.$ Пусть $P, Q$ и $R -$ точки пересечения прямых $BF$ и $CK;$ $CK$ и $AM;$ $AM$ и $BF$ соответственно. В базисе из векторов $overline$ и $overline$ найти координаты векторов $overline,$ $overline$ и $overline.$

2.37. На плоскости заданы векторы $e_1(-1,2),$ $e_2(2,1)$ и $a(0,-2).$ Убедиться, что базис $B=e_1, e_2$ в множестве всех векторов на плоскости Построить заданные веткоры и найти разложение вектора $a$ по базису $B.$

Ответ: $a=-frace_1-frace_2.$

2.38. Показать, что тройка векторов $e_1(1,0,0), e_2(1,1,0)$ и $e_3(1,1,1)$ образуют базис в множестве всех векторов пространства. Вычислить координаты вектора $a=-2i-k$ в базисе $B(e_1, e_2, e_3)$ и написать соответствующее разложение вектора по базису.

Видео:Базис. Разложение вектора по базису.Скачать

Разложить вектор по базису онлайн

Любой вектор некоторого -мерного пространства можно представить в виде линейной комбинации базисных векторов этого -мерного пространства и при том единственным образом.

Разложение произвольного -мерного вектора по базису, образованному линейно-независимой системой -мерных векторов выглядит следующим образом:

, где &#x2212 некоторые числа, являющиеся коэффициентами разложения (линейной комбинации) вектора по базису .

Наш онлайн калькулятор найдет разложение вектора по базису с подробным решением на русском языке.