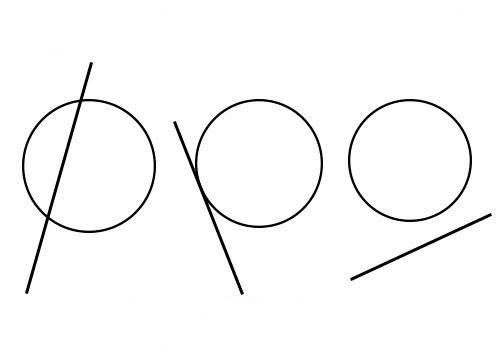Расположение точки относительно вектора

Вступление

Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.

Начнем с взаимного расположения точки относительно прямой, луча и отрезка.

Задача №1

Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.

Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P₁(x₁, y₁), P₂(x₂, y₂). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P₁P₂ и P₁M и по его знаку сделать вывод.

Задача №2

Определить принадлежит ли точка лучу.

Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P₁(x₁, y₁) — начало луча, а P₂(x₂, y₂) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P₁(x₁, y₁), где P₂(x₂, y₂) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (P₁P₂, P₁M) ≥ 0 – скалярное произведение (точка лежит на луче)

Задача №3

Определить принадлежит ли точка отрезку.

Решение
Пусть точки P₁(x₁, y₁), P₂(x₂, y₂) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P₁, P₂. Далее нам нужно определить лежит ли точка между точками P₁ и P₂, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP₁, MP₂). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P₁(x₁, y₁), P₂(x₂, y₂) необходимо и достаточно выполнения условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (MP₁,MP₂) ≤ 0 – скалярное произведение (точка лежит между P₁ и P₂)

Задача №4

Взаимное расположение двух точек относительно прямой.

Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.

Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] 0 – точки лежат по одну сторону.
3. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] = 0 – одна (или две) из точек лежит на прямой.

Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] ≤ 0.

Задача №5

Определить пересекаются ли две прямые.

Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a₁x + b₁y + c₁ = 0 и a₂x + b₂y + c₂ = 0. Тогда условие параллельности прямых заключается в том, что a₁b₂ — a₂b₁ = 0.
Если же прямые заданы точками P₁(x₁, y₁), P₂(x₂, y₂), M₁(x₃, y₃), M₂(x₄, y₄), то условие их параллельности заключается в проверки косого произведения векторов P₁P₂ и M₁M₂: если оно равно нулю, то прямые параллельны.

В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b₁, a₁), (-b₂, a₂) которые называются направляющими векторами.

Задача №6

Определить пересекаются ли два отрезка.

Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:

Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P₁P₂, P₁M₂] > 0, [P₁P₂, P₁M₁] [P₁P₂, P₁M₂] * [P₁P₂, P₁M₁] 2 + b 2 ).

Задача №8

Расстояние от точки до луча.

Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.

В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.

Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP₁P₂ – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
1. (P₁M, P₁P₂) 2 .

Теперь рассмотрим случай, когда центр второго круга O₂ находится между точками O₁ и C. В этом случае получим отрицательное значение величины d₂. Использование отрицательного значения d₂ приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.

Заключение

Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.

Видео:Как построить точки в системе координат OXYZСкачать

Взаимное расположение прямых в пространстве. Взаимное расположение точки и прямой

Базовыми геометрическими элементами являются точка, прямая и плоскость. Они называются так потому, что из них можно построить многие объекты, например, такие как пирамида или призма. Чтобы понять свойства этих фигур, важно знать взаимное расположение в пространстве прямых и плоскостей. Рассмотрим подробнее этот вопрос в статье.

Видео:Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

Определение и описание точки, прямой и плоскости

Вам будет интересно: Пополняем словарный запас: неказистый — это.

Точкой в геометрии называется 0-мерный объект, единственной характеристикой которого являются его координаты. Последние представляют собой набор чисел, привязанный к конкретной системе. Например, на плоскости он состоит из двух элементов, в трехмерном пространстве — из трех.

Прямая — это одномерный объект, который обладает некоторым направлением. Если соединить ее любые две точки, то получится вектор, который ее характеризует. Для описания прямых используют несколько типов уравнений, которые с помощью несложных математических операций могут быть переведены друг в друга. Здесь приведем лишь векторное, которое часто применяется для анализа взаимного расположения в пространстве прямых. Оно для трехмерного случая принимает форму:

Вам будет интересно: «Соразмерно» — это и «в рамках», и «гармонично»

(x; y; z) = (x0; y0; z0) + α*(a; b; c)

Элементы с нулевыми индексами соответствуют некоторой точке, которая является частью прямой. Координаты, которые умножаются на параметр α (альфа) описывают ее направляющий вектор, вдоль которого она проходит. Подставляя произвольные числа α можно найти все точки, которые образуют прямую в пространстве.

Очевидно, что для векторного уравнения в двумерном пространстве необходимо использовать лишь две координаты для точек и векторов.

Плоскость является совокупностью точек. Образованные на них вектора перпендикулярны некоторому направлению, задаваемому нормальным к плоскости вектором. Все это можно описать несколькими способами. Тем не менее, для решения задач на определение взаимного расположения плоскости и прямой удобно пользоваться уравнением общего вида. Оно записано ниже:

A*x + B*y + C*z + D = 0

Удобство этой формы записи заключается в том, что коэффициенты A, B, C являются координатами перпендикулярного вектора n¯ к плоскости.

При решении задач важно учитывать, в каком пространстве решается проблема. Так, приведенный вид уравнения плоскости в двумерном случае без координаты z будет соответствовать уравнению прямой.

Видео:Координаты точки и координаты вектора 1.Скачать

Расположение точки и прямой

Вам будет интересно: Обзор основных вузов Сургута

Взаимное расположение этих объектов не зависит от того, рассматриваются они на плоскости или в пространстве. Критерии определения постоянно одни и те же.

Относительно прямой точка может находиться лишь в двух возможных положениях:

• лежать на ней;
• либо не принадлежать ей.

Определить вариант расположения в конкретной задаче достаточно легко. Для этого следует подставить координаты искомого объекта в уравнение, задающее прямую. Если равенство будет выполняться, значит, точка принадлежит прямой. В противном случае она не является ее частью.

Видео:Разложение вектора по базису. 9 класс.Скачать

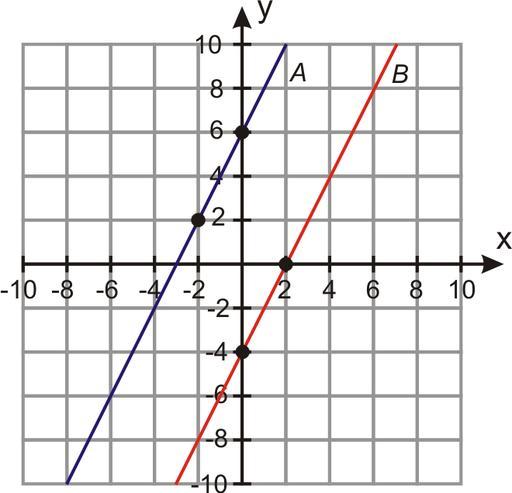
Две прямые на плоскости

Какое может быть взаимное расположение двух прямых на плоскости? Существует три разных варианта:

Они совпадают друг с другом. То есть пересекаются во всех точках.

Чтобы понять, каково взаимное расположение прямых в конкретном случае, необходимо провести некоторый математический анализ. Ниже описываются основные идеи, которые следует использовать при его осуществлении.

Если направляющие векторы прямых параллельны друг другу, значит и прямые, как минимум, будут параллельными. Параллельность векторов доказывается, если один из них можно представить в виде другого, умноженного на действительное число.

Если направляющие вектора параллельны, и хотя бы одна точка одной прямой соответствует и другой прямой, тогда речь идет о полностью совпадающих прямых.

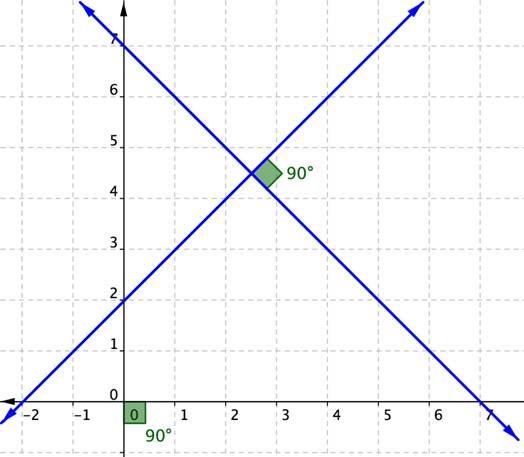
Если направляющие вектора не являются параллельными, то прямые пересекаются в одной точке. Найти ее координаты можно с помощью решения системы уравнений (эти координаты должны соответствовать обоим уравнениям прямых).

Частным случаем пересечения прямых является угол пересечения, равный 90o. В таком случае говорят о перпендикулярности между рассматриваемыми объектами. Если две прямые перпендикулярны, то скалярное произведение их векторов направляющих будет равно нулю.

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Прямая и окружность на плоскости

Поскольку данный объект часто появляется в геометрических задачах, то полезно также рассмотреть вопрос взаимного расположения окружности и прямой. Возможны такие варианты:

Она разделяет ее на две дуги. То есть прямая пересекает окружность в двух точках.

Определить вариант расположения этих объектов для конкретной задачи можно с использованием соответствующих уравнений. Для окружности с центром в (x0; y0) и радиусом R оно имеет вид:

Определение варианта расположения сводится к решению квадратного уравнения.

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Две прямые в пространстве

Часто возникает вопрос о том, каково взаимное расположение прямых в пространстве трехмерном. Возможны те же самые варианты, что описаны в предыдущем пункте, однако, к ним добавляется еще один. Скрещивающиеся прямые и не пересекаются, и не являются параллельными. Подробнее — ниже.

Определить, являются ли рассматриваемые одномерные объекты скрещивающимися, также не представляет особого труда. В первую очередь, необходимо выяснить, что их направляющие векторы не параллельные. После этого проще всего рассчитать расстояние между прямыми. Если оно равно нулю, значит, они пересекаются, если отличается (больше или меньше) — тогда они скрещивающиеся.

Расчет расстояния производится по формуле:

• v¯ — направляющий вектор первой прямой;
• M1M2¯ — вектор, построенный на произвольных точках M1 и M2 первой и второй прямой соответственно.

Формулу можно непосредственно применить, если даны векторные уравнения прямых.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

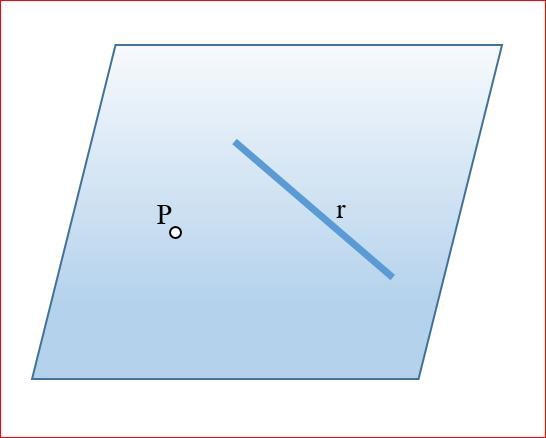
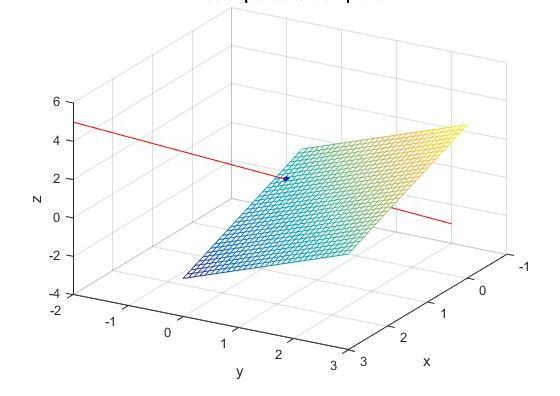
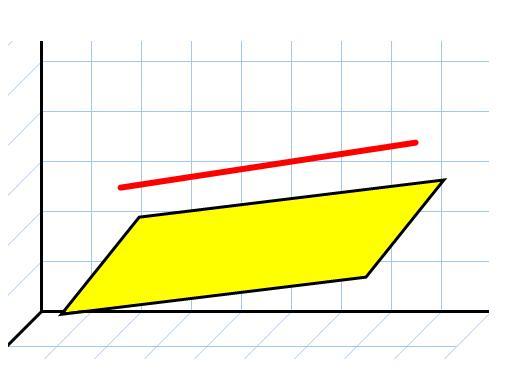
Плоскость и прямая

В данном случае речь идет о трехмерном пространстве. Взаимное расположение плоскости и прямой возможно следующее:

Прямая пересекает плоскость.

Определить параллельность этих геометрических объектов достаточно просто. Для этого нужно рассчитать скалярное произведение нормального вектора плоскости и направляющего вектора прямой. Равенство нулю этого произведения является достаточным условием параллельности. Если к тому же хотя бы одна точка принадлежит плоскости, значит, вся прямая лежит в ней.

Если скалярное произведение нулю не равно, тогда вывод следующий. Прямая и плоскость пересекаются в одной точке. Частным случаем является пересечение под прямым углом. Если направляющий вектор прямой можно представить в виде произведения на число вектора нормали к плоскости, значит, прямая и плоскость перпендикулярны.

Видео:Координаты вектора. 9 класс.Скачать

Задача с двумя прямыми на плоскости

Ниже даны два уравнения в общем виде для прямых в двумерном пространстве:

Необходимо определить взаимное расположение прямых.

Поскольку имеет место случай на плоскости, то нет необходимости приводить эти уравнения к векторному виду. Решить задачу можно проще, если найти корни системы из этих них. Имеем:

2*x — y = 7 => y = 2*x — 7;

-3*x + 2*y = 0 => -3*x + 2*(2*x — 7) = 0 =>

Поскольку система имеет единственное решение, то оно соответствует пересечению рассматриваемых прямых в точке (14; 21).

Видео:Прямоугольная система координат в пространстве. 11 класс.Скачать

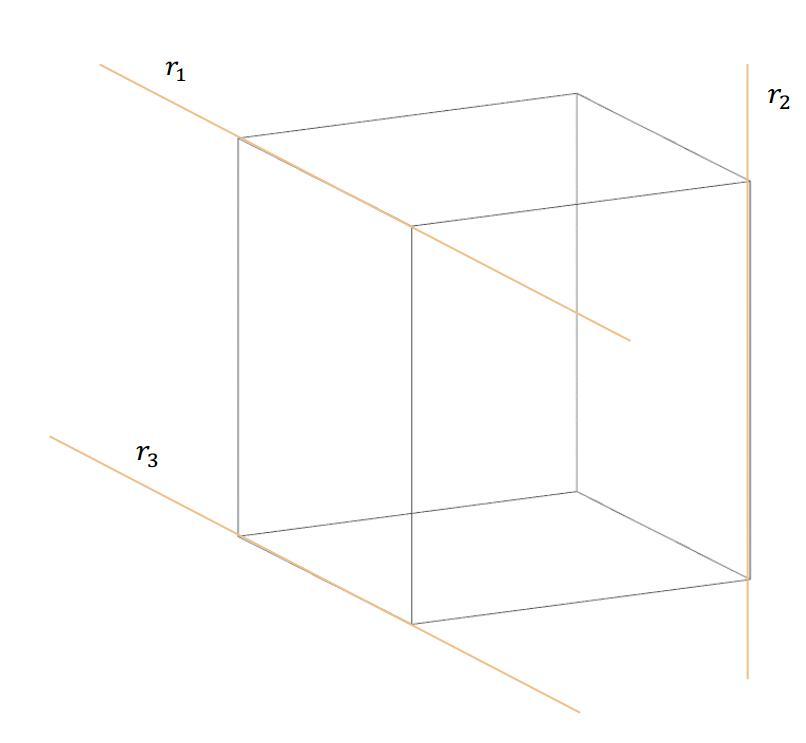
Задача с двумя прямыми в пространстве

Даны две прямые, которые описываются уравнениями:

r1: (x; y; z) = (1 ; -2; 0 ) + α*(2; -1; 1);

r2: (x; y; z) = (2; 2; 1) + β*(0; 3; -1).

Каково взаимное расположение прямых в пространстве?

Можно заметить, что направляющие вектора параллельными не являются (никакое значение параметра β не способно дать направляющий вектор r1). То есть прямые либо пересекаются, либо являются скрещивающимися.

Вычислим расстояние между ними. Для этого на r1 возьмем точку M1(1; -2; 0), а на r2 — точку M2(2; 2; 1). Тогда вектор, соединяющий их, равен:

Его векторное произведение с направляющим вектором для r1 равно:

Поскольку длина этого вектора отлична от нуля, значит, расстояние между прямыми будет больше нуля. Последний факт говорит, что они не имеют общих точек и являются скрещивающимися.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Кинематика. Задание положения точки.

Положение точки в пространстве можно задать двумя способами: координатным и векторным.

При задании движения координатным способом с телом отсчета связывают какую-либо систему координат, например, декартовую. Движение точки М будет задано в том случае, если ее координаты будут известны, как функции времени:

Эти зависимости называются уравнениями движения точки в декартовых координатах. Они выражают текущие координаты движущейся точки в виде функций времени. Если точка движется, оставаясь все время в одной плоскости, можно ограничиться двумя уравнениями движения: x = x(t), y = y(t).

Видео:2.4. Радиус-вектор и вектор перемещенияСкачать

Векторный способ задания положения точки .

Допустим, М – движущаяся точка относительно тела отсчета А. В теле А в качестве точки отсчета выберем произвольную точку О и построим вектор Этот вектор называется радиус-вектором точки М.

Радиус-вектор – это вектор, соединяющий начало отсчета с положением точки в любой момент времени.

Когда точка М движется, радиус-вектор непрерывно изменяется во времени, поэтому существует некоторая вектор-функция времени Зная эту функцию, для каждого времени t можно построить вектор и тем самым найти положение движущейся точки в данный момент. Функция называется векторным законом (векторным уравнением) движения точки М.

Точка задается радиус-вектором, если известны его длина (модуль) и направление в пространстве, другими словами – значения его проекций r_x, r_y, r_z на оси координат OX, OY и OZ, или углы между радиус-вектором и осями координат. При рассмотрении движения на плоскости:

Здесь за мы принимаем модуль радиус-вектора , а r_x и r_y являются его проекциями на оси координат, все три величины скалярны, x и y – координаты точки А.

Из этих уравнений видно, что между координатным и векторным способами задания положения точки существует связь.

🔥 Видео

Великий Тихий океан и доисторическая Земля.Скачать

Михаил Галактионов в гостях у Леонида Слуцкого | Коммент.ТренерСкачать

Как разложить вектор по базису - bezbotvyСкачать

Положение точек в пространствеСкачать

Синдром Бругада и инфаркт миокарда без обструктивного поражения коронарных артерийСкачать

Векторы. Метод координат. Вебинар | МатематикаСкачать

11 класс, 1 урок, Прямоугольная система координат в пространствеСкачать

Проецирование точки на 3 плоскости проекцийСкачать