Радиус вектор центра масс системы (8 видео)

3.5. Центр масс

Снова рассмотрим ту же систему материальных точек. Построим радиус-вектор по следующему правилу:

где — радиус-вектор — той материальной точки системы, а — ее масса.

Радиус-вектор определяет положение в пространстве центра инерции (центра масс) системы.

Вовсе не обязательно, что в центре масс системы окажется какая-то материальная точка.

Пример. Найдем центр масс системы, состоящей из двух маленьких шариков — материальных точек, соединенных невесомым стержнем (рис. 3.29). Такая система тел называется гантелей.

Рис. 3.29. Центр масс гантели

Из рис. видно, что

Подставляя в эти равенства выражение для радиус-вектора центра масс

Отсюда следует, что центр масс лежит на прямой, проходящей через центры шаров. Расстояния l₁ и l₂ между шарами и центром масс равны соответственно

Центр масс ближе к тому шарику, масса которого больше, что видно из отношения:

Определим, с какой скоростью движется центр инерции системы. Дифференцируем по времени обе части:

В числителе полученного выражения в правой части стоит сумма импульсов всех точек, то есть импульс системы. В знаменателе стоит полная масса системы

Мы получили, что скорость центра инерции связана с импульсом системы и ее полной массой таким же соотношением, какое справедливо для материальной точки:

Видео 3.11. Движение центра масс двух одинаковых тележек, связанных пружиной.

Таким образом, можно считать, что скорость V_C является скоростью системы как целого. Она, разумеется, может отличаться от скоростей каждого из тел, входящих в систему.

Центр масс замкнутой системы движется всегда с постоянной скоростью, поскольку импульс такой системы сохраняется.

Если продифференцировать теперь выражение для импульса системы по времени и учесть, что производная импульса системы есть равнодействующая внешних сил, то получим уравнение движения центра масс системы в общем случае:

Центр масс системы движется точно так же, как двигалась бы материальная точка с массой, равной массе всех частиц системы, под действием векторной суммы всех внешних сил, приложенных к системе.

Если имеется система материальных точек, внутреннее расположение и движение которых нас не интересует, мы вправе считать ее материальной точкой с координатами радиус-вектора центра инерции и массой, равной сумме масс материальных точек системы.

Если связать с центром масс замкнутой системы материальных точек (частиц) систему отсчета (ее называют системой центра масс), то полный импульс всех частиц в такой системе окажется равным нулю. Таким образом, в системе центра масс замкнутая система частиц как целое покоится, и существует только движение частиц относительно центра масс. Поэтому ясно выявляются свойства внутренних процессов, протекающих в замкнутой системе.

В случае, когда системой является тело с непрерывным распределением масс, определение центра масс остается по существу тем же. Окружаем произвольную точку в нашем теле небольшим объемом . Масса, заключенная в этом объеме, равна , где — плотность вещества тела, которая может и не быть постоянной по его объему. Сумма по всем таким элементарным массам заменяется теперь на интеграл по всему объему тела, так что для положения центра масс тела получается выражение

Если вещество тела однородно, плотность его постоянна, и ее можно вынести из-под знака интеграла, так что она сократится в числителе и знаменателе. Тогда выражение для радиус-вектора центра масс тела принимает вид

где — объем тела.

И в случае непрерывного распределения масс справедливо утверждение, что

Центр масс твердого тела движется так, как двигалась бы материальная точка с массой, равной массе тела, под действием векторной суммы всех внешних сил,приложенных к телу.

Пример. Если снаряд взрывается в некоторой точке своей параболической траектории, то осколки летят по самым различным траекториям, но его центр масс продолжает движение по параболе.

Содержание

Определение центра масс
Радиус-вектор и координаты центра масс
Скорость центра масс
Примеры задач на определение центра масс
Движение центра масс системы
Движение центра масс: основная теорема
Практическое значение теоремы о движении центра масс
💥 Видео

Видео:3.3. Центр масс и закон его движения | Динамика | Александр Чирцов | ЛекториумСкачать

Определение центра масс

При исследовании поведения систем частиц, часто удобно использовать для описания движения такую точку, которая характеризует положение и движение рассматриваемой системы как единого целого. Такой точкой служит центр масс.

Для однородных тел обладающих симметрией центр масс часто совпадает с геометрическим центром тела. В однородном изотропном теле одной выделенной точке найдется симметричная ей точка.

Видео:Центр массСкачать

Радиус-вектор и координаты центра масс

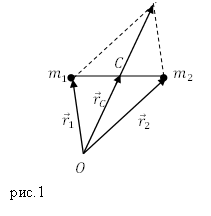
Предположим, что у нас имеются две частицы с равными массами, им соответствуют радиус-векторы: $<overline>_1 и <overline>_2$ . В этом случае центр масс расположен посередине между частицами. Центр масс (точка C) определён радиус-вектором $<overline>_C$ (рис.1).

Из рис.1 видно, что:

Можно ожидать, что вместе с геометрическим центром системы радиус-вектор, которого равен $<overline>_C,$ играет роль точка, положение которой определяет распределение массы. Ее определяют так, чтобы вклад каждой частицы был пропорционален ее массе:

Радиус -вектор $<overline>_C$, определенный выражением (2) — средне взвешенная величина радиус-векторов частиц $<overline>_1$ и $<overline>_2$. Это становится очевидным, если формулу (2) представить в виде:

Выражение (3) показывает, что радиус-вектор каждой частицы входит в $<overline>_C$ с весом, который пропорционален его массе.

Выражение (3) легко обобщается для множества материальных точек, которые расположены произвольным образом.

Если положения N материальных точек системы задано при помощи их радиус-векторов, то радиус — вектор, определяющий положение центра масс находим как:

Выражение (4) считают определением центра масс системы.

При этом абсцисса центра масс равна:

Ордината ($y_c$) центра масс и его аппликата ($z_c$):

Формулы (4-7) совпадают с формулами, которые используют для определения тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.

Видео:Урок 79. Центр масс тела и методы определения его положенияСкачать

Скорость центра масс

Выражение для скорости центра масс ($<overline>_c=frac<d<overline>_c>

$) запишем как:

где $overline

$ — суммарный импульс системы частиц; $M$ масса системы. Выражение (8) справедливо при движениях со скоростями которые существенно меньше скорости света.

Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.

Видео:Система материальных точек. Центр масс. Закон движения центра масс. Видеоурок по физике 10 классСкачать

Примеры задач на определение центра масс

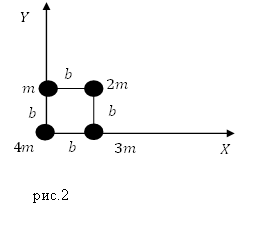
Задание. Система составлена из материальных точек (рис.2), запишите координаты ее центра масс?

Решение. Рассмотрим рис.2. Центр масс системы лежит на плоскости, значит, у него две координаты ($x_c,y_c$). Найдем их используя формулы:

Вычислим массу рассматриваемой системы точек:

Тогда абсцисса центра масс $x_ $равна:

Ответ. $x_c=0,5 b$; $y_с=0,3 b$

Задание. Космонавт, имеющий массу $m$, неподвижен относительно корабля массы $M$. Двигатель космического аппарата выключен. Человек начинает подтягиваться к кораблю при помощи легкого троса. Какое расстояние пройдет космонавт ($s_1$), какое корабль ($s_2$) до точки встречи? В начальный момент расстояние между ними равно $s$.

Решение. Центр масс корабля и космонавта лежит на прямой, соединяющей эти объекты.

В космосе, где внешние силы отсутствуют, центр масс замкнутой системы (корабль-космонавт) либо покоится, либо движется с постоянной скоростью. В избранной нами (инерциальной) системе отсчета он покоится. При этом:

Видео:Радиус-векторыСкачать

Движение центра масс системы

Допустим, что у нас есть некоторая система, состоящая из n -ного количества материальных точек. Возьмем одну из них и обозначим ее массу как m k . Приложенные к точке внешние силы (как активные силы, так и реакции связей) имеют равнодействующую F k e . Внутренние силы имеют равнодействующую F k l . Наша система находится в движении, следовательно, нужная точка будет иметь ускорение a k . Зная основной закон динамики, мы можем записать следующую формулу:

m k a k = F k e + F k l .

Ее можно применить к любой точке системы. Значит, для всей системы целиком можно сформулировать следующие уравнения:

m 1 a 1 = F 1 e + F 1 l , m 2 a 2 = F 2 e + F 2 l , ⋯ m n a n = F n e + F n l .

Данная формула состоит из дифференциальных уравнений, описывающих движение системы в векторной форме. Если мы спроецируем эти равенства на соответствующие координатные оси, то у нас получатся дифференциальные уравнения движения в проекциях. Но в конкретных задачах чаще всего вычислять движение каждой точки системы не требуется: можно ограничиться характеристиками движения всей системы в целом.

Видео:Определение центра масс #shorts #физика #егэСкачать

Движение центра масс: основная теорема

Характер движения системы можно определить, зная закон, по которому движется ее центр масс.

Центр инерции системы (центр масс) – это воображаемая точка с радиус-вектором R , выражаемым через радиус-векторы r 1 , r 2 , . . . соответствующих материальных точек по формуле R = m 1 r 1 + m 2 r 2 + . . . + m n r n m .

Здесь сумма показателей в числителе m = m 1 + m 2 + . . . + m 3 выражает общую массу всей системы.

Для нахождения этого закона нам нужно взять уравнения движения системы, приведенные в предыдущем пункте, и сложить их правые и левые части. У нас получится, что:

∑ m k a k ¯ = ∑ F k ¯ e + ∑ F k ¯ l .

Взяв формулу радиус-вектора центра масс, получим следующее:

Теперь возьмем вторую производную по времени:

Здесь буквой a c ¯ обозначено ускорение, которое приобретает центр масс системы.

Свойство внутренних сил в системе гласит, что F k l равно нулю, значит, окончательное равенство будет выглядеть так:

M a c ¯ = ∑ F k ¯ e .

Это уравнение является записью закона движения центра масс. Запишем его:

Движение центра масс системы идентично движению материальной точки той же массы, что и вся система целиком, к которой приложены все действующие на систему внешние силы.

Иначе говоря, произведение ускорения центра масс системы на массу самой системы будет равно геометрической сумме всех внешних сил, действующих на эту систему.

Возьмем полученное выше уравнение и спроецируем его правую и левую части на соответствующие координатные оси. У нас получится:

M x c ¨ = ∑ F k x ¯ e , M y c ¨ = ∑ F k y ¯ e , M z c ¨ = ∑ F k z ¯ e .

Эти равенства являются дифференциальными уравнениями движения центра масс в проекции на оси в декартовой системе координат.

Видео:Движение центра масс твердого телаСкачать

Практическое значение теоремы о движении центра масс

Данная теорема имеет большую практическую ценность. Поясним, в чем именно она заключается.

Любое тело, движущееся поступательно, может быть рассмотрено в качестве материальной точки, масса которой равна массе всего тела. Во всех других случаях такой подход возможен лишь тогда, когда для определения положения тела в пространстве нам будет достаточно знать, в каком положении находится его центр масс. Также важно, чтобы условия задачи допускали исключение вращательной части движения тела.
С помощью теоремы движения центра масс системы мы можем не рассматривать в задачах неизвестные нам заранее внутренние силы.

Разберем пример применения теоремы для решения практической задачи.

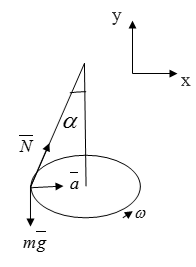
Условие: к оси центробежной машины на нити подвешено кольцо из металла. Оно совершает равномерные вращательные движения с угловой скоростью, равной ω . Вычислите, на каком расстоянии центр кольца находится от оси вращения.

Решение

Очевидно, что система находится под воздействием силы тяжести N N ¯ α α . Также необходимо учесть силу натяжения нити и центростремительное ускорение.

Второй закон Ньютона для системы будет выглядеть так:

Теперь создадим проекции обеих частей равенства на оси абсцисс и ординат и получим:

N sin α = m a ; N cos α = m g .

Мы можем разделить одно уравнение на другое:

Поскольку a = υ 2 R , υ = ω R , то нужное нам уравнение будет выглядеть так: