Если на одной прямой отложены равные отрезки и через их концы проведены параллельные (8 видео)

Если на одной прямой отложены равные отрезки и через их концы проведены параллельные

§ 47. СВОЙСТВО ОТРЕЗКОВ, ОТСЕКАЕМЫХ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ
НА СТОРОНАХ УГЛА.

Теорема. Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие другую сторону угла, то и на этой стороне угла отложатся равные между собой отрезки.

Пусть на стороне АВ угла АВN отложены равные отрезки ВМ = МК = КС (черт. 248) и через точки деления М, К и С проведены параллельные прямые, пересекающие сторону ВN того же угла.

На этой стороне образовались три отрезка: ВМ’, М’К’ и К’С’. Требуется доказать, что
ВМ’ = М’К’ = К’С’.

Для доказательства через точки М’ и К’ проведём прямые, параллельные АВ. Мы получим треугольники ВММ’, М’ЕК’ и К’РС’. Сравним эти треугольники.

Сначала сравним треугольники МВМ’ и М’ЕК’. В этих треугольниках имеем:
/ 1 = / 2, как соответственные углы при параллельных ВА и М’Е и секущей ВN;
/ 3 = / 4, как острые углы 1 с соответственно параллельными сторонами (АВ||М’Е и
ММ’ || КК’).
ВМ = МК по построению;
МК = М’Е, как противоположные стороны параллелограмма.
————————————————————————
1 Углы 1-й и 4-й могут оказаться оба тупыми, но и в этом случае они останутся равными, а потому доказательство теоремы не изменится .

Следовательно, ВМ = М’Е. Таким образом, / ВММ’ = / М’ЕК’ (по стороне и двум прилежащим к ней углам). Отсюда следует, что ВМ’ = М’К’ .

Так же можно доказать, что ВМ’ = К’С’, т. е. ВМ’ = М’К’ = К’С’. При доказательстве теоремы мы откладывание отрезков начали от вершины угла, но теорема справедлива и для того случая, когда откладывание отрезков будет начато не от вершины угла, а от любой точки его стороны. (Докажите это самостоятельно.)

В этом случае вершину угла на чертеже можно не отмечать (черт. 249).

Теорема справедлива и для случая, когда прямые КО и МР параллельны.

Задача. Разделить данный отрезок на п равных частей.

Пусть отрезок АВ (черт. 250) нужно разделить на 5 равных частей. Для этого из точки. А под каким-нибудь углом к отрезку АВ проведём луч и от вершины А отложим на нём последовательно 5 равных отрезков. Конец последнего отрезка, точку С₅, соединим отрезком прямой с точкой В и через точки деления С₁, С₂, С₃, С₄ проведём прямые, параллельные ВС₁. Эти прямые разделят данный отрезок на 5 равных частей.

Подобным образом всякий отрезок можно разделить на любое число равных частей.

Содержание

Теорема Фалеса
Как пользоваться теоремой Фалеса на практике
Обратная теорема Фалеса
Доказательство теоремы Фалеса
Кто впервые доказал теорему о пропорциональных отрезках
Теорема Фалеса. Если на одной из двух прямых отложены последовательно равные отрезки и через их концы проведены параллельные прямые, пересекающие вторую. — презентация
Похожие презентации
Презентация на тему: » Теорема Фалеса. Если на одной из двух прямых отложены последовательно равные отрезки и через их концы проведены параллельные прямые, пересекающие вторую.» — Транскрипт:
🎬 Видео

Видео:Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать

Теорема Фалеса

Одна из основополагающих теорем (теорема Фалеса) в геометрии говорит о том, что проведенные через концы одинаковых отрезков прямой параллельные линии отсекают на другой прямой тоже одинаковые по длине отрезки. Причем происходит это независимо от угла между прямыми. Это достаточно произвольная формулировка теоремы Фалеса, но достаточно емко описывающая ее суть. Разные учебники приводят разные формулировки, но суть остается неизменной.

Ключевые слова в теореме (при любой формулировке) — прямые, отрезки, равные, пропорциональные, параллельные. Это говорит о том, что теорема Фалеса касается только планиметрии, то есть изображения линий на плоскости. Она очень важна для картографии и навигации, широко используется в архитектуре и живописи, строительстве и проектировании.

Классической формулировки, единой в своем роде нет. Например, формулировку можно услышать в такой редакции:

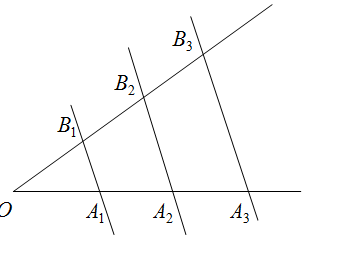
Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.

А можно и в такой:

Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Если внимательно присмотреться, то можно увидеть, что одно утверждение не противоречит другому, а рисунки практически идентичны. Если продолжить прямые на первом рисунке по получим тот же угол.

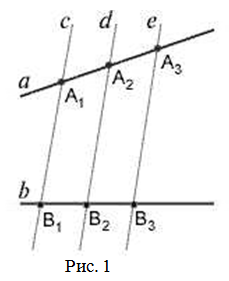
Кроме прямых, которые проходят под углом, такая же картина происходит при пересечении параллельных прямых. Разница состоит в том, что на пересекающихся прямых отрезки АВ и А₁В₁ могут быть как одинаковыми, так и пропорциональными, в зависимости от угла наклона секущих. А для случая параллельных — только одинаковыми. Если обобщить два случая, то обобщенная теорема Фалеса звучит так: Параллельные прямые отсекают на секущих пропорциональные отрезки.

Для иллюстрации можно воспользоваться рисунком 1.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Как пользоваться теоремой Фалеса на практике

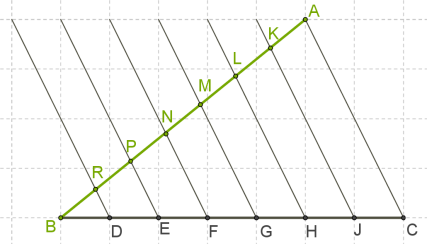
Теорема Фалеса это не только теоретическое утверждение, доказанное методами математики, но и практический инструмент для построения различных фигур. Простейшая задача — разделить на равные части произвольный отрезок ВА. Пусть этих частей будет 7.

Для решения задачи нарисуем отрезок ВС, образующий с данным ВА угол. Как видим, отрезок ВС проходит вдоль клеток на бумаге, что позволяет выбрать на нем равные отрезки. В нашем случае, это:

BD=DE=EF=FG=GH=HJ=JC.

Начиная от крайних точек А и С проведем параллельные линии, пересекающие отрезок ВА. На нем тоже получиться семь равных отрезков: BR=RP=PN=NM=ML=LK=KA.

С таким же успехом мы можем разделить отрезок на 5, 6, 4 или любое другое количество равных частей. Суть метода состоит в том, что длину отрезка ВС мы заведомо выбираем такой, чтобы его можно было легко разделить на заданное количество частей. Например, длина отрезка ВА 37 см, а его нужно разделить на 5 частей. Выбираем длину отрезка ВС в 25 см, отмечаем точки и выполняем построение по теореме Фалеса.

Видео:№385. Докажите теорему Фалеса: если на одной из двух прямых отложить последовательноСкачать

Обратная теорема Фалеса

Не менее широко используется и теорема, названная обратной. То есть, доказательства требует не равность или пропорциональность отрезков, а параллельность прямых. Формулируется обратная теорема Фалеса так:

Если две или более прямых (a, b, c) отсекают от двух других прямых (d, f) равные или пропорциональные отрезки, то они параллельные.

Утверждение справедливо, независимо от того, параллельные d, f или пересекаются.

Видео:Теорема Фалеса #j2m #математика #теоремаСкачать

Доказательство теоремы Фалеса

Математика, тем более, геометрия, наука точная. Каждое утверждение, кроме аксиом, требует доказательства. В геометрии под термином «теорема» подразумевается утверждение, которое доказано на базе ранее полученных знаний в виде аксиом и других теорем.

Теорема Фалеса с доказательством приведена в большинстве учебников. В отличие от теоремы Пифагора, доказательств у нее меньше, но все они четкие, понятные и аргументированные. Покажем одно из них.

Не будем повторять формулировок, продемонстрируем только ход мыслей и выполним необходимые построения:

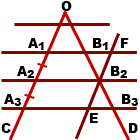
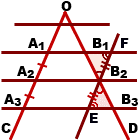
Выберем точку В₂ и проведем прямую, параллельную стороне угла ОС. При этом отмечаем, что А₁А₃ || EF. Рассматривая четырехугольник

А₁FЕА₃ замечаем, что А₁F и ЕА₃ параллельны по определению, а А₁А₃ и FВ₃ параллельны по построению. Отсюда вытекает, что А₁ FЕА ₃ — параллелограм и А₁А₃ = EF.

Аналогичным образом доказываем равенство других сторон и получаем, что по равенству вертикальных и внутренних углов ∠B₁B₂F=∠B₃B₂E и ∠B₂FB₁=∠B₂EB₃ треугольники B₂B₁F и B₂B₃E равны, откуда вытекает, что B₁B₂=B₂B₃.

Именно это и требовалось доказать.

Видео:Геометрия 8. Урок 8 - Теорема Фалеса - теорияСкачать

Кто впервые доказал теорему о пропорциональных отрезках

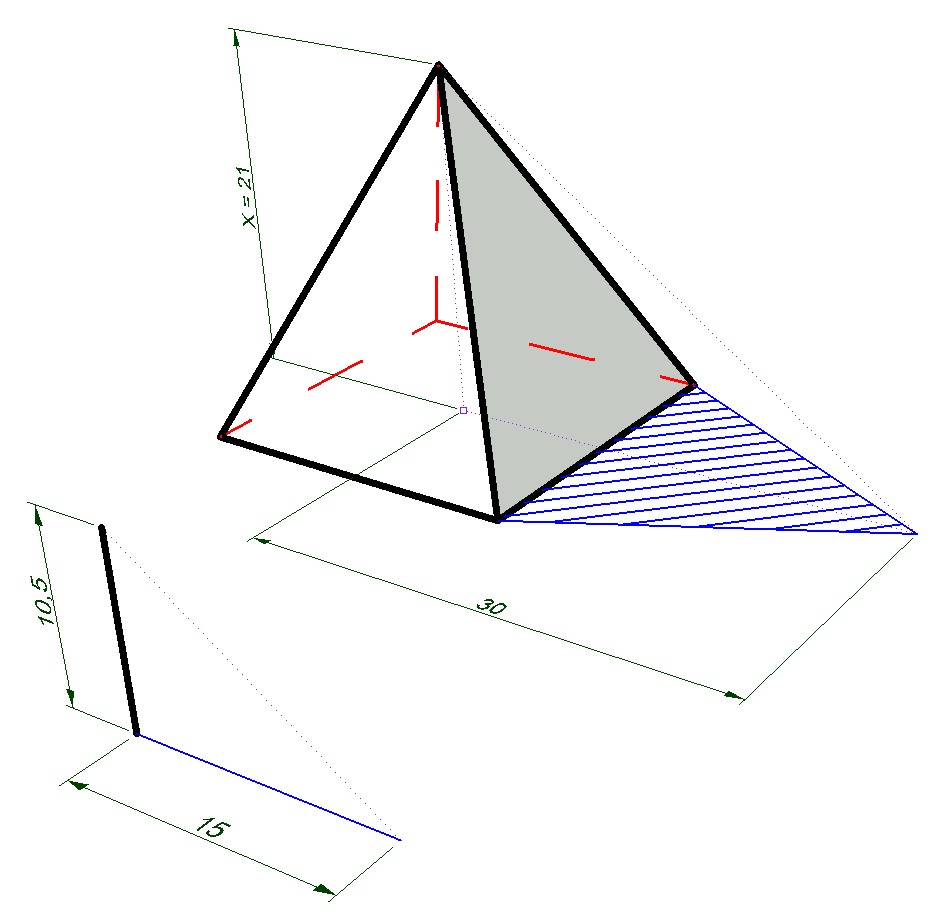
По легенде, впервые на практике использовал теорему греческий философ Фалес Милетский. Он применил ее для измерения высоты пирамиды Хеопса, пользуясь падающей на песок тенью. Для сравнения длины отрезков использовалась воткнутая рядом палка.

Но доказательство теоремы, самое давнее из известных, зафиксированных в письменных источниках, дано в книге «Элементы» другого философа и математика — Эвклида. Тем не менее, утверждение получило имя Фалеса, под которым известно до сих пор.

Видео:Теорема Фалеса. 8 класс.Скачать

Теорема Фалеса. Если на одной из двух прямых отложены последовательно равные отрезки и через их концы проведены параллельные прямые, пересекающие вторую. — презентация

Презентация была опубликована 8 лет назад пользователемКирилл Лошкомоев

Презентация на тему: » Теорема Фалеса. Если на одной из двух прямых отложены последовательно равные отрезки и через их концы проведены параллельные прямые, пересекающие вторую.» — Транскрипт:

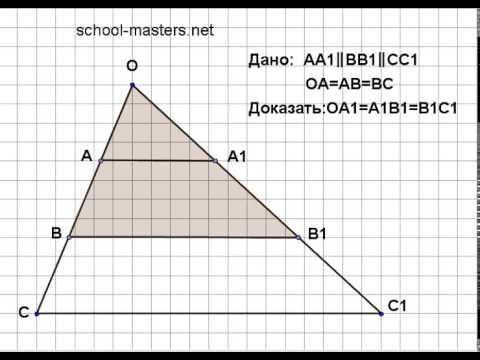
2 Если на одной из двух прямых отложены последовательно равные отрезки и через их концы проведены параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. I случай А1А1 А2А2 А3А3 А4А4 В1В1 В2В2 В3В3 В4В4 Дано: прямые А 1 А 4 и В 1 В 4 параллельны. А 1 А 2 = А 2 А 3 =А 3 А 4, прямые А 1 В 1, А 2 В 2, А 3 В 3 и А 4 В 4 параллельны. Доказать: В 1 В 2 = В 2 В 3 = В 3 В 4 Доказательство. Четырехугольники А 2 А 1 В 1 В 2 и А 3 А 2 В 2 В 3 параллелограммы по определению. Значит, А 1 А 2 =В 1 В 2 и А 2 А 3 =В 2 В 3 как противоположные стороны параллелограмма. Но А 1 А 2 =А 2 А 3, поэтому В 1 В 2 =В 2 В 3. Аналогично доказывается,что В 2 В 3 =В 3 В 4. Следовательно В 1 В 2 = В 2 В 3 = В 3 В 4

3 Если на одной из двух прямых отложены последовательно равные отрезки и через их концы проведены параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. II случай А1А1 А2А2 А3А3 А4А4 В1В1 В2В2 В3В3 В4В4 Дано: прямые А 1 А 4 и В 1 В 4 не параллельны. А 1 А 2 = А 2 А 3 =А 3 А 4, прямые А 1 В 1, А 2 В 2, А 3 В 3 и А 4 В 4 параллельны. Доказать: В 1 В 2 = В 2 В 3 = В 3 В 4 Доказательство. С D Через точку В 2 проведем прямую CD, параллельную прямой А 1 А 4. СВ 2 =В 2 D ( I случай) (накрест лежащие при параллельных прямых А 1 В 1 и А 3 В 3 и секущей CD). (вертикальные). Значит, по второму признаку. Следовательно В 1 В 2 =В 2 В 3. Аналогично доказывается, что В 2 В 3 =В 3 В 4. Следовательно В 1 В 2 = В 2 В 3 = В 3 В 4