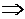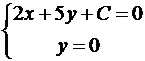Провести параллельную прямую на расстоянии

Альтернативная формула:
Прямая, проходящая через точку M₁(x₁; y₁) и параллельная прямой Ax+By+C=0 , представляется уравнением

назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения параллельной прямой (см. также как составить уравнение перпендикулярной прямой).

Пример №2 . Написать уравнение прямой, параллельной прямой 2x + 5y = 0 и образующей вместе с осями координат треугольник, площадь которого равна 5.
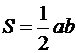
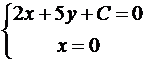
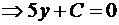
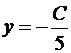
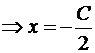
Решение. Так как прямые параллельны, то уравнение искомой прямой 2x + 5y + C = 0. Площадь прямоугольного треугольника , где a и b его катеты. Найдем точки пересечения искомой прямой с осями координат:
;
.
Итак, A(-C/2,0), B(0,-C/5). Подставим в формулу для площади: 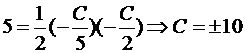. Получаем два решения: 2x + 5y + 10 = 0 и 2x + 5y – 10 = 0 .

Пример №3 . Составить уравнение прямой, проходящей через точку (-2; 5) и параллельной прямой 5x-7y-4=0 .
Решение. Данную прямую можно представить уравнением y = 5 /₇x – 4 /₇ (здесь a = 5 /₇). Уравнение искомой прямой есть y – 5 = 5 / 7(x – (-2)), т.е. 7(y-5)=5(x+2) или 5x-7y+45=0 .

Пример №4 . Решив пример 3 (A=5, B=-7) по формуле (2), найдем 5(x+2)-7(y-5)=0.

Пример №5 . Составить уравнение прямой, проходящей через точку (-2;5) и параллельной прямой 7x+10=0.
Решение. Здесь A=7, B=0. Формула (2) дает 7(x+2)=0, т.е. x+2=0. Формула (1) неприменима, так как данное уравнение нельзя разрешить относительно y (данная прямая параллельна оси ординат).

Видео:Построение параллельной плоскости на расстояние 30 мм.Скачать

Провести параллельную прямую на расстоянии

ГЛАВА III.
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ

§ 41. ПРАКТИЧЕСКИЕ РАБОТЫ НА МЕСТНОСТИ.

1. Проведение параллельных прямых на местности.

Пусть нам нужно провести прямую, параллельную имеющейся изгороди АВ (черт. 218), на данном от неё расстоянии, например на расстоянии 20 м.

Для решения этой практической задачи провешим с помощью эккера из точки С прямую, перпендикулярную к прямой АВ, и на ней отложим отрезок СD длиной 20 м. В точке D установим эккер так, чтобы направление одного бруска эккера совпало с направлением СD.

По направлению второго бруска эккера провешим прямую МN. Она будет параллельна прямой АВ.

Докажите это с помощью какого-либо признака параллельности двух прямых линий, приняв СD за секущую прямых АВ и МN.

2. Съёмка плана земельного участка, имеющего форму многоугольника.

а) Съёмка плана земельного участка, имеющего форму треугольника.

Пусть нам нужно начертить план земельного участка, имеющего форму треугольника, стороны которого равны, например, 120 м, 95 м и 70м (черт. 219).

Приняв масштаб миллиметр за один метр, построим треугольник, стороны которого соответственно равны 120мм, 95мм и 70мм.

Получим план данного нам земельного участка, построенный в масштабе, равном 0,001.

При вычерчивании плана масштаб должен выбираться в зависимости от размеров участка и от размеров листа бумаги, на котором будет изображён план.

б) Съёмка плана земельного участка, имеющего форму четырёхугольника.

Пусть требуется начертить план четырёхугольного участка, стороны которого равны, например, 200 м, 180 м, 160 м и 195 м (черт. 220). Провешим диагональ этого четырёхугольника, например АС, и измерим ее длину. Пусть она будет равна 210 м.

Выбрав подходящий масштаб, построим сначала один треугольник, например треугольник АBС, а затем к стороне АС пристроим второй треугольник АDС. В результате получим план данного нам участка, построенный в выбранном масштабе.

Если надо начертить план земельного участка, имеющего форму пятиугольника или шестиугольника, то поступаем так же: разбиваем этот многоугольник на треугольники, измеряем длины их сторон, выбираем подходящий масштаб и последовательно строим треугольники, располагая их на чертеже в том же порядке, как они расположены на самом земельном участке.

3. Определение расстояния между двумя точками, одна из которых недоступна.

Чтобы определить расстояние между точками A и В, разделёнными рекой (черт. 221), строим при точке В с помощью эккера прямой угол АВN.

На прямой BN откладываем последовательно два равных отрезка ВС и СD. Точки С иD отмечаем вехами. При точке D строим прямой угол ВDК. Продолжение отрезка АС пересечёт прямую DK в некоторой точке Е. DЕ = АВ. Доказать самостоятельно правильность решения.

4. Определение расстояния между двумя доступными точками,
разделёнными препятствием (черт. 222).

Пусть требуется определить расстояние между точками А и В. Провешим произвольную прямую, примем её за ось симметрии и построим с помощью эккера точки А’ и В’, симметричные заданным. Отрезок, соединяющий построенные точки,.имеет искомую длину, т. е. А’В’ = АВ.

1. На школьном дворе провести прямую, параллельную какой-нибудь данной прямой (изгороди, забору, стене школьного здания).

2. Отметить вехами где-нибудь вблизи школы земельный участок треугольной формы и начертить его план.

3. Начертить план какого-нибудь земельного участка четырёхугольной формы (например, школьного участка или участка, занимаемого огородом, садом; или предварительно на открытой ровной площадке обозначить вехами вершины какого-нибудь четырёхугольника и нанести его на план).

Видео:Параллельные прямые циркулемСкачать

Построение параллельных прямых

Вы будете перенаправлены на Автор24

В основе способов построения параллельных прямых с помощью различных инструментов лежат признаки параллельности прямых.

Видео:6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Построение параллельных прямых с помощью циркуля и линейки

Рассмотрим принцип построения параллельной прямой, проходящей через заданную точку, с помощью циркуля и линейки.

Пусть дана прямая и некоторая точка А, которая не принадлежит данной прямой.

Необходимо построить прямую, проходящую через заданную точку $А$ параллельно данной прямой.

На практике зачастую требуется построить две или более параллельных прямых без данной прямой и точки. В таком случае необходимо начертить прямую произвольно и отметить любую точку, которая не будет лежать на данной прямой.

Рассмотрим этапы построения параллельной прямой:

1. Выберем произвольную точку на данной прямой и назовем ее $В$. обратим внимание, что выбор точки абсолютно произвольный, т.к. не влияет на результат построения.
2. С помощью циркуля и начертим окружность радиуса $АВ$ с центром в точке $В$.

На пересечении окружности и прямой отметим точку и назовем ее $С$.

С тем же радиусом $АВ$ построим окружность с центром в точке $С$. Обратим внимание, что вторая построенная окружность обязательно должна пройти через точку В при правильном выполнении построения.

С прежним радиусом $АВ$ построим третью окружность с центром в точке $А$.

Отметим точку пересечения второй и третьей построенных окружностей и назовем ее $D$. Отметим, что третья окружность при правильном построении также должна пройти через точку $В$.

Через точки $А$ и $D$ проведем прямую, которая будет параллельной заданной.

Таким образом, получили параллельные прямые $ВС$ и $АD$:

$BC parallel AD$, т. $A in AD$.

На практике также применяют метод построения параллельных прямых с помощью чертежного угольника и линейки.

Готовые работы на аналогичную тему

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Построение параллельных прямых с помощью угольника и линейки

Для построения прямой, которая будет проходить через точку М параллельно данной прямой а, необходимо:

1. Угольник приложить к прямой $а$ диагональю (смотрите рисунок), а к его большему катету приложить линейку.
2. Передвинуть угольник по линейке до тех пор, пока данная точка $М$ не окажется на диагонали угольника.
3. Провести через точку $М$ искомую прямую $b$.

Мы получили прямую, проходящую через заданную точку $М$, параллельную данной прямой $а$:

$a parallel b$, т. $M in b$.

Параллельность прямых $а$ и $b$ видна из равности соответственных углов, которые отмечены на рисунке буквами $alpha$ и $beta$.

Видео:Построение прямой, параллельной даннойСкачать

Построение параллельной прямой, отстоящей на заданное расстояние от данной прямой

В случае необходимости построения прямой, параллельной заданной прямой и отстоящей от нее на заданном расстоянии можно воспользоваться линейкой и угольником.

Пусть дана прямая $MN$ и расстояние $а$.

1. Отметим на заданной прямой $MN$ произвольную точку и назовем ее $В$.
2. Через точку $В$ проведем прямую, перпендикулярную к прямой $MN$, и назовем ее $АВ$.
3. На прямой $АВ$ от точки $В$ отложим отрезок $ВС=а$.
4. С помощью угольника и линейки проведем прямую $CD$ через точку $С$, которая и будет параллельной заданной прямой $АВ$.

Если отложить на прямой $АВ$ от точки $В$ отрезок $ВС=а$ в другую сторону, то получим еще одну параллельную прямую к заданной, отстоящую от нее на заданное расстояние $а$.

Видео:Как провести параллельную прямуюСкачать

Другие способы построения параллельных прямых

Еще одним способом построения параллельных прямых является построение с помощью рейсшины. Чаще всего данный способ используют в чертежной практике.

При выполнении столярных работ для разметки и построения параллельных прямых, используется специальный чертежный инструмент – малка – две деревянные планки, которые скрепляются шарниром.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 22 07 2021

🌟 Видео

Параллельность прямой к плоскостиСкачать

Построение параллельной плоскости на расстояние 40 мм. Плоскость задана со следами.Скачать

Построение параллельных прямыхСкачать

Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать

Параллельные прямые. 6 класс.Скачать

Параллельные линии в AutoCADСкачать

4K Как начертить параллельные прямые при помощи циркуля, how to draw parallel linesСкачать

19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Построение прямой, параллельной даннойСкачать

24. Параллельные линии могут пересекаться. Такое возможно?Скачать

7 класс, 38 урок, Расстояние от точки до прямой. Расстояние между параллельными прямымиСкачать

Определение расстояние между параллельными прямыми (Способ замены плоскостей проекции).Скачать

КАК ПОСТРОИТЬ ПАРАЛЛЕЛЬНУЮ ПРЯМУЮ ЧЕРЕЗ ЗАДАННУЮ ТОЧКУ? Примеры | МАТЕМАТИКА 6 классСкачать

Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать